自適應濾波器在現(xiàn)代數(shù)字信號處理中的應用極為廣泛，分成系統(tǒng)辨識,、逆模型,、預測和干擾消除4大類別[1]。對于實時性要求很高的場合，往往需要使用硬件設計自適應濾波器,?；?a class="innerlink" href="http://forexkbc.com/tags/FPGA" title="FPGA" target="_blank">FPGA的自適應濾波器近年來被不斷地研究和改進。

　　使用FPGA中的邏輯單元(LE)很容易實現(xiàn)乘累加(MAC)運算,，從而將采用最小均方(LMS)算法的自適應濾波器直觀地映射到FPGA上,。但是，基于MAC方案的自適應濾波器的時鐘頻率會很高,，功耗會很大,。ALLRED D J等人提出了利用雙LUT結(jié)構(gòu)的DA方案來實現(xiàn)LMS自適應濾波器[2]，雖然提高了吞吐量,，降低了功耗,，但其控制模塊、地址循環(huán)設置都比較復雜,；Guo Rui等人提出采用單LUT結(jié)構(gòu)的DA方案來實現(xiàn)LMS自適應濾波器[3],，盡管節(jié)省了近一半的LE，但其處理速度有所下降,，并且偏移二進制編碼（OBC）的硬件編程頗為復雜,。

　　本文提出了基于雙LUT模塊的特殊DA方案，旨在將LMS順序執(zhí)行算法更高效地映射到FPGA上,，充分利用了DA的基本特性以及對LMS算法的改進來達到節(jié)省資源,、提高速度的目標。

1 自適應濾波器的算法

　　設x(n)和w(n)分別表示自適應濾波器的輸入信號和權(quán)值向量,，定義：x(n)=[x(n),，x(n-1)，…,，x(n-L+1)]T,，w(n)=[w0(n)，w1(n),，…,，wL-1(n)]T，則LMS算法的基本形式如下,。

　　濾波輸出：

　　其中,，y(n)是自適應濾波器的輸出信號，d(n)是期望信號,，e(n)表示誤差信號,，是收斂因子，L是自適應濾波器的抽頭數(shù),。雖然LMS算法僅涉及乘法,、加減和迭代3種運算,，但它是一種嚴格順序執(zhí)行的自適應算法[1]。倘若利用MAC方案直接將LMS自適應濾波器映射到FPGA上,，編程雖然簡單，但難以發(fā)揮FPGA并行處理的優(yōu)勢,。

　　延遲最小均方（DLMS）算法是對LMS算法的一種改進,，該算法最大的優(yōu)點就是可以并行執(zhí)行[4]。本文所使用的DLMS算法的權(quán)值更新公式為：

　　而濾波輸出,、誤差計算公式與LMS算法相同,。由式(4)知，對第k個權(quán)值wk(n)進行迭代更新時,，必須對相應的x(n)延遲k個采樣周期,，k=0，1,，…,，L-1。圖1給出了DLMS自適應濾波器的模塊圖,。

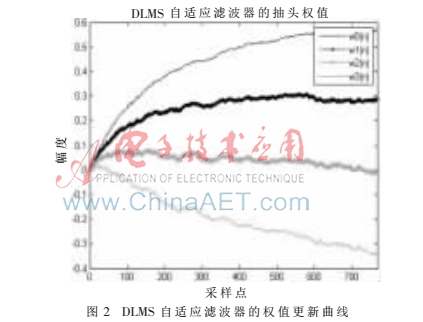
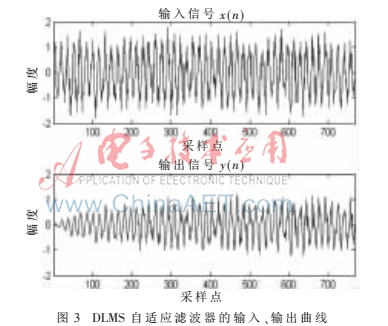
　　圖2,、圖3分別給出了4抽頭DLMS自適應濾波器的抽頭權(quán)值以及輸入、輸出信號的Matlab仿真曲線,。由圖2知,，自適應濾波器的4個抽頭權(quán)值的總體變化趨勢漸趨平緩。由圖3知,，輸出信號相對于輸入信號而言抖動幅度逐漸變小,，而且愈發(fā)類似于正弦信號。但由于該自適應濾波器只有4個抽頭,，輸入信號的信噪比只有3 dB,，所以自適應濾波器的權(quán)值在520個采樣點以后才比較平緩，并且輸出信號與期望信號之間仍存在較明顯的差別,。若能提高自適應濾波器的抽頭數(shù),，或改用信噪比更高的輸入信號，則會加快抽頭權(quán)值的平緩速度,，并且輸出信號將更加接近正弦信號,。

2 特殊DA方案

　　在使用DA方案優(yōu)化基于FPGA的權(quán)值固定的經(jīng)典濾波器時，首先把濾波器的權(quán)值系數(shù)有規(guī)律地存儲在LUT模塊中,，然后利用輸入信號的二進制形式從最低位到最高位逐一訪問LUT模塊的存儲條目,，最后對LUT模塊的各個輸出量進行移位、累加運算,，得到最終的濾波輸出結(jié)果[5],。而自適應濾波器的權(quán)值是不斷更新變化的,，必須對存儲在LUT模塊中的權(quán)值進行迭代更新，這時可以考慮使用兩個LUT模塊聯(lián)合運作,。

　　設輸入信號x(n)被量化成B bit二進制補碼的形式,，最左邊一位是符號位，則：

　　Qj存儲在LUT模塊中時沒有正負之別,，在LUT模塊輸出端的后面引入一個符號控制端來判定對Qj做加法還是減法[6],。該LUT模塊定義為核心查找表(K-LUT)。

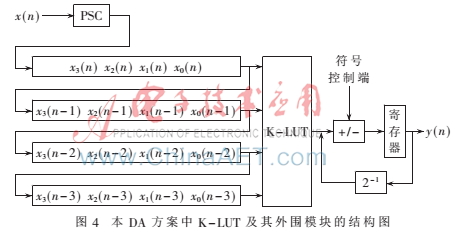
　　圖4給出了L=4,、B=4的DLMS自適應濾波器設計中K-LUT及其外圍模塊的結(jié)構(gòu)圖,。圖中的PSC模塊表示并/串轉(zhuǎn)換器，2-1模塊表示右移器,。

　　K-LUT的第r個條目的更新式如下：

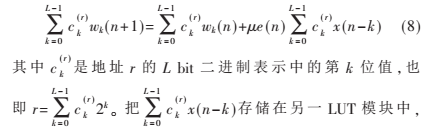　　該LUT模塊定義為輸入查找表（I-LUT）,。當檢測到自定義的中間信號clk_data的上升沿時，新的輸入信號將被讀入,，I-LUT的內(nèi)容隨即自動更新,。

　　對于L=4、B=4的情況,，由Quartus II集成開發(fā)軟件的時序仿真結(jié)果知,，clk_data的周期應設置成為時鐘信號clk周期的6倍。第n時刻I-LUT的各個條目存儲內(nèi)容如表1所示,。當n+1時刻來臨時,，x(n)、x(n-1),、x(n-2),、x(n-3)自動變成x(n+1)、x(n),、x(n-1),、x(n-2)。

　　一旦n時刻I-LUT的內(nèi)容更新并且y(n),、e(n),、e(n)的計算都已完成，那么K-LUT的內(nèi)容將被更新,。通過設置合適的clk_data周期來保證K-LUT(n)到K-LUT(n+1)的更新在n+1時刻到來之前全部完成,。式(8)則變?yōu)椋?/p>

　　K-LUT(r)(n+1)=K-LUT(r)(n)+?滋e(n)I-LUT(r)(n)(9)

　　K-LUT的更新步驟如下：(1)讀取K-LUT(n)和I-LUT(n)中具有相同存儲地址的條目；(2)用e(n)乘以I-LUT(n)的輸出,；(3)將步驟(2)中的乘積與K-LUT(n)的輸出進行求和運算,；(4)將步驟(3)中的和存儲到K-LUT(n+1)中相同存儲地址的條目。其中?滋和e(n)相乘是通過對e(n)進行移位運算實現(xiàn)的,，值選成2的冪,。

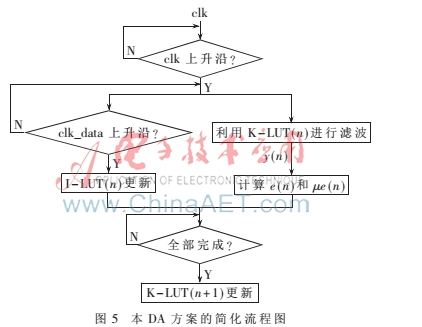
　　圖5為本DA方案的簡化流程圖,，可以看出I-LUT的更新由clk_data控制，而濾波運算,、誤差計算,、e(n)的乘積運算都由clk控制。

3 基于FPGA實例驗證

　　由于FPGA中的LUT通常具有4個輸入端,，共24個存儲條目,，故本文以設計4階基于FPGA的DLMS自適應濾波器為例，這樣使用兩個LUT模塊就能實現(xiàn)最基本,、最小規(guī)模的自適應濾波器。其他的高階設計都以4階為基礎,。

　　表2給出了分別采用MAC方案和本DA方案設計出的DLMS自適應濾波器的各項性能指標,。這里取1/4。必須指出,，系統(tǒng)時鐘clk的最高頻率與系統(tǒng)功耗密切相關(guān),，頻率越高，功耗越大,；用于控制輸入信號讀取速度的clk_data的最高頻率表征了DLMS自適應濾波器的處理速度,。

　　由表2知，本DA方案設計出的DLMS自適應濾波器不但消耗了更少的LE和寄存器數(shù)量,，而且獲得了更低的功耗和更高的處理速度,，優(yōu)勢明顯。表3給出了同樣采用本DA方案但值不同時的DLMS自適應濾波器的性能比較,。

　　由表3知,，取不同值時采用本DA方案設計DLMS自適應濾波器所消耗的LE和寄存器數(shù)目是相同的，所以在保證DLMS算法收斂前提下,，的取值不會影響設計自適應濾波器所消耗的硬件資源,，但是自適應濾波器的功耗和處理速度會有少許差別。

　　本文提出的特殊DA方案的基本結(jié)構(gòu)主要包含K-LUT和I-LUT模塊,，重點討論了4階DLMS自適應濾波器的設計方案,。通過驗證，采用本DA方案設計基于FPGA的DLMS自適應濾波器相對于MAC方案具有更高的處理速度和更低的資源消耗,。本方案推廣到更高階設計時,，總體思路不變，但最好要對K-LUT和I-LUT模塊進行分解,，具體辦法有待進一步探究,。

參考文獻

　　[1] HAYKIN S.自適應濾波器原理(第四版)[M].鄭寶玉，譯.北京：電子工業(yè)出版社,，2010.

　　[2] ALLRED D J,，HEEJONG Y,，KRISHNAN V，et al.A novel high performance distributed arithmetic adaptive filter imple-mentation on FPGA[J].IEEE Signal Processing,，2004,，5(5)：161-165.

　　[3] Guo Rui，DEBRUNNER L S.A novel adaptive filter imple-mentation scheme using distributed arithmetic[J].IEEE Signals,，Systems and Computers,，2011，6(11)：160-164.

　　[4] Long Guozhu,，Ling Fuyun,，PROAKIS J G.The LMS algorithmwith delayed coefficient adaptation[J].IEEE Transactions on Acoustics，Speech and Signal Processing,，1989,，37(9)：1397-1405.

　　[5] UWE M B.Digital signal processing with field programmablegate arrays[M].Third Edition.Germany Berlin：Springer- Verlag，2007.

　　[6] ALLRED D J,，YOO H,，KRISHNAN V，et al.LMS adaptive filters using distributed arithmetic for high throughput[J].IEEE Transactions on Circuits and Systems,，2005,，52(7)：1327-1337.