Widrow和Hoff等人于1960年提出最小均方誤差(LMS)算法,，由于其結(jié)構(gòu)簡單,，計算量小,，穩(wěn)定性好,，易于實現(xiàn)等優(yōu)點而得到廣泛的應(yīng)用,。LMS算法的缺點是收斂速度慢，它克服不了收斂速度和穩(wěn)態(tài)誤差這一對固有矛盾：在收斂的前提下,，如果步長取較大值,，雖然收斂速度能得到提高，但穩(wěn)態(tài)誤差會隨之增大,，反之穩(wěn)態(tài)誤差雖然降低但收斂速度就會變慢,。為解決這一矛盾，人們提出了許多改進型自適應(yīng)算法,。其中很大一類是變步長LMS算法,。文獻[4]提出Sigmoid函數(shù)變步長LMS算法(SVSLMS)。該算法在初始階段或未知系統(tǒng)的系數(shù)參數(shù)發(fā)生變化時,，其步長較大,，從而使該算法有較快的收斂速度；而在算法收斂后,，不管主輸入端干擾信號e(n)有多大,，都保持很小的調(diào)整步長，從而獲得較小的穩(wěn)態(tài)失調(diào)噪聲,。但Sigmoid函數(shù)過于復雜,，且在誤差e(n)接近零處變化太大，不具有緩慢變化的特性,，使得SVSLMS算法在自適應(yīng)穩(wěn)態(tài)階段仍有較大的步長變化,；文獻[5]提出的算法引入了多個調(diào)整參數(shù)，因而步長因子不易設(shè)計和控制,；文獻[6-8]提出了3種與誤差信號成非線性關(guān)系的步長設(shè)計方法,，該類算法具有較好的收斂性能，但3種算法在計算步長因子時,，都存在指數(shù)運算,。在數(shù)字信號處理中，進行一次指數(shù)運算需要的計算量,，相當于進行多次乘法運算的計算量,。
因此這類算法在實現(xiàn)時，增大了計算復雜度,。為克服上述變步長LMS自適應(yīng)濾波器存在的不足,，在此提出了一種新的變步長LMS自適應(yīng)濾波算法，該算法具有良好的收斂性能,，較快的收斂速度,，較小的穩(wěn)態(tài)誤差．良好的魯棒性,，并且在求變步長因子時計算量較小。
1 新的變步長LMS算法分析
基本的固定步長LMS算法的迭代公式可以表述為：
式中：X(n)表示時刻n的輸入信號矢量,；W(n)表示時刻n自適應(yīng)濾波器的權(quán)系數(shù),；d(n)是期望輸出值；e(n)是誤差,；μ是控制穩(wěn)定性和收斂速度的參量(步長因子),。本文基于文獻[6，7]建立一個步長μ(n)和誤差e(n)的函數(shù)關(guān)系：反正切函數(shù)是一個關(guān)于自變量的增函數(shù),，且在零附近變化平緩,，而且是一個有界函數(shù)，函數(shù)值不會發(fā)散,。根據(jù)W(k+1)=W(k)=w*=最佳Wiener解,，即2μ(n)e(n)X(n)=0并且0<μ(n)<1／λmax，即∣e(n)X(n)∣=0,，求得e(n)最小值,。
根據(jù)上述討論，可將新算法的變步長μ(n)取為：
μ(n)=βαtan(α∣e(n)X(n)∣)
初始時刻∣e(n)X(n)∣很大,，由于反正切是一個自變量的增函數(shù),，所以μ(n)較大；隨著算法不斷地向穩(wěn)態(tài)趨近,，∣e(n)X(n)∣不斷減小,，μ(n)也隨之不斷減小,；當達到穩(wěn)態(tài)時,，∣e(n)X(n)∣很小，μ(n)也很小,，此時的穩(wěn)態(tài)失調(diào)誤差也很小,。
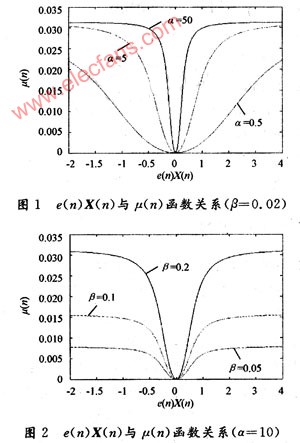
由圖1可看出α越大，相同誤差水平時的步長也越大,，但在誤差接近為零時步長變化越劇烈,。圖2是β取不同值時的步長變化曲線，可以看出隨著β的減小步長也在減小,。
2 仿真及結(jié)果分析
下面通過計算機仿真來驗證算法的收斂性能,。仿真條件為：自適應(yīng)濾波器的階數(shù)為L=2；未知系統(tǒng)的FIR系數(shù)為W=[0,，0]T,；參考輸入信號x(n)是零均值，方差為1的高斯白噪聲,；v(n)為與x(n)不相關(guān)的高斯白噪聲,。分別做200次獨立的仿真，采樣點數(shù)為1 000,，然后求其統(tǒng)計平均,，得出學習曲線。
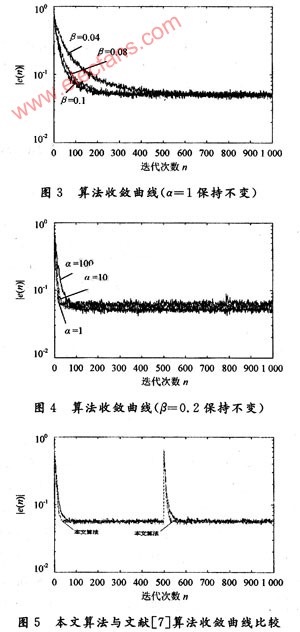
圖3是α固定,，不同β值對應(yīng)的收斂曲線,。隨著β值的增大，算法的收斂速度逐漸加快,。圖4是β保持不變,，不同α值對應(yīng)的收斂曲線，隨著α逐漸減小,，算法的誤差也隨之減小,，但達到穩(wěn)態(tài)的時間逐漸增加。
文獻[7]提出了一種改進的變步長LMS算法,，其步長變化為e(n)X(n)的函數(shù)：
μ(n)=β[1-exp(-α∣e(n)x(n)∣2)]
該算法取α=15,，β=0.3。圖5是在第500個采樣點時刻未知系統(tǒng)發(fā)生時變,，系數(shù)矢量變?yōu)閃=[0.2,，0.5]T時本文算法與文獻[7]算法的比較，分別做500次獨立的仿真,，然后求其統(tǒng)計平均,，得出學習曲線?？梢钥闯霰疚乃鏊惴ň哂懈斓氖諗克俣?，更快地回到穩(wěn)態(tài)，說明此算法具有更好的魯棒性,，并且計算量更小,。
本文使用TI公司的TMS320C5402芯片，該芯片采用哈佛體系結(jié)構(gòu),，具有高度并行性,，同時擁有高度集成的指令系統(tǒng)，簡化編成過程,，模塊化結(jié)構(gòu)程序設(shè)計增強了程序的可移植性,。
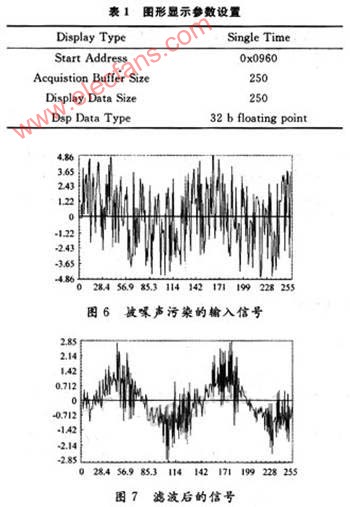
程序在CCS環(huán)境下編譯，鏈接生成公共目標代碼文件,，再load到DSP中運行,。本文采用C語言編程。圖6為被噪聲污染的輸入信號,，圖7為濾波后的信號,。比較兩圖可以看出,，混合信號經(jīng)過本文算法處理后噪聲得到了很好的抑制，而原始信號得到了明顯的加強和改善,。
3 在DSP上的具體實現(xiàn)
4 結(jié)語
本文提出了一種新的變步長LMS算法,。該算法通過對最佳Wiener解的分析，并用反正切函數(shù)建立了步長因子μ(n)與誤差e(n)的非線性函數(shù)關(guān)系,。本算法具有初始階段和未知系統(tǒng)時變階段步長自動增大而穩(wěn)態(tài)時步長很小的特點,，且具有良好的魯棒性和較小的計算量。通過在DSP上的實現(xiàn),，說明此算法具有可實行,，并且實現(xiàn)方法簡單，濾波效果好,。