劉梅芷,，柳曉鳴,，索繼東

　　（大連海事大學(xué) 信息科學(xué)技術(shù)學(xué)院,，遼寧 大連 116026）

　　摘  要： 針對不同分布海雜波的抑制及目標檢測問題,，首次將自適應(yīng)噪聲對消器應(yīng)用在海雜波的處理中，并且將此對消器與小波分解理論相結(jié)合來抑制海雜波,，提取出目標,。首先，對含有目標的海雜波信號進行小波分解。然后,，類比自適應(yīng)噪聲對消器模型,，設(shè)計一種自適應(yīng)雜波對消器。將經(jīng)小波分解后的信號作為自適應(yīng)雜波對消器的輸入信號,，經(jīng)過自適應(yīng)雜波對消器輸出的信號即為雜波抑制的結(jié)果,。最后，通過MATLAB仿真,，分析采用不同的小波基函數(shù)和不同的分解層數(shù)的雜波抑制效果,，驗證此種算法對于海雜波抑制的有效性。

　　關(guān)鍵詞： 小波分解,；自適應(yīng)濾波器,；雜波對消器；海雜波抑制,；計算機仿真

　　0 引言

　　在航海雷達接收的信號中,，通常包含雷達雜波信號和目標信號。如果沒有雜波的干擾,，雷達會很容易完成探測任務(wù),。同時，如果有雜波的存在,，就會存在信雜比,，這會影響到對目標信號的檢測。尤其是在一些強海雜波背景中,，由于目標信號很微弱,，會淹沒在海雜波中，所以對雷達雜波的抑制能力提出了更高的要求,。雷達雜波抑制處理一直是雷達信號處理領(lǐng)域中的一個熱門研究課題,。目前，雜波抑制的方法有很多,，但都未盡善盡美,。因此，找出一種簡單又實用的雜波抑制方法很重要[1],。

　　在雷達雜波中主要有四種雜波：海雜波,、雨雪雜波、噪聲和雷達同頻干擾,。其中,，海雜波是最主要的干擾，它的相關(guān)性最強,，所以是最難處理的雜波,。

　　小波變換是一個時間和頻率的局部變換，即在高頻部分具有較高的時間分辨率和較低的頻率分辨率，在低頻部分具有較低的時間分辨率和較高的頻率分辨率,，這就使得小波變換具有對信號的自適應(yīng)性,。它能夠有效地從信號中提取信息，通過伸縮和平移等運算功能對函數(shù)或信號進行多尺度細化分析,。適合用小波變換進行分析的信號應(yīng)該具有不穩(wěn)定性,，尤其是對于那些急劇變化的高度不穩(wěn)定信號效果較好。應(yīng)用小波分解可以將雜波從含有目標的雜波中提取出來,，但不是最佳的雜波成分估計,。

　　本文首次采用了將小波分解與自適應(yīng)濾波器相結(jié)合的方法來抑制雜波，類比于自適應(yīng)噪聲對消器設(shè)計了一個自適應(yīng)雜波對消器,，將含有目標的雜波作為自適應(yīng)雜波對消器的主信道輸入,，將小波分解出的雜波成分作為參考信道輸入。這樣,，輸出信號即為雜波抑制結(jié)果。最后通過MATLAB進行實踐仿真[2],。

　　1 基于小波分解的自適應(yīng)濾波算法

　　1.1 海雜波信號的小波分解算法

　　在對雷達雜波信號進行小波變換時,，必須對連續(xù)小波加以離散化。離散小波函數(shù)可寫作：

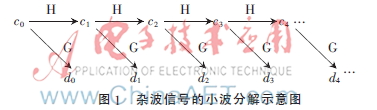
　　根據(jù)Mallat算法,，對雷達雜波信號f（n）進行小波分解,，可以得到信號的平滑項和信號的小波系數(shù)項，如圖1所示,。其中[3]：

　　經(jīng)過小波分解后的平滑項表征雷達雜波信號中的各尺度的低頻成分隨時間的變化特性,，即表征雜波的能量空間分布特性；小波系數(shù)項表征雷達雜波信號中的各尺度的高頻成分隨時間的變化特性,，即表征雜波的方差成分,。平滑項相當于雷達信號的低頻成分，選擇適當?shù)某叨?，便可以找到有效的抑制雜波的低頻成分的處理方法,；而小波系數(shù)項相當于雷達信號的高頻成分，通過所提出的自適應(yīng)對消方法,，便可得到有效的抑制[4],。

　　1.2 自適應(yīng)雜波對消器

　　通過分析自適應(yīng)噪聲對消器，對其進行類比推廣得到自適應(yīng)雜波對消器,，這樣就可以實現(xiàn)對雜波的抑制,。

　　在自適應(yīng)噪聲對消器中噪聲是需要消除的，通過去除噪聲來逼近理想信號,。然而在包含目標的海雜波中也有著類似的情況,，需要想辦法抑制甚至消除海雜波來得到理想目標。通過對比，將自適應(yīng)噪聲對消器加以改進可以得出自適應(yīng)雜波對消器,，如圖2所示,。圖2中用作雜波補償?shù)膮⒖驾斎雗1進入自適應(yīng)濾波器后輸出y，經(jīng)和主輸入s+n0相減,，得到系統(tǒng)的輸出e=s+n0-y,。如果n0=y，則系統(tǒng)的輸出就是有效信號s,；當n0與y十分相近時,，系統(tǒng)的輸出等于有效信號s與殘余干擾量n0-y之和。為了使此殘余干擾量達到最小,，將系統(tǒng)的輸出反饋到自適應(yīng)濾波器,。根據(jù)實際情況，選擇合適的自適應(yīng)濾波算法得到濾波器的權(quán)值,，使得系統(tǒng)的總輸出功率達到最小[5],。

　　1.3 自適應(yīng)濾波算法的選擇

　　自適應(yīng)濾波的原理就是利用前一時刻已獲得的濾波參數(shù)等結(jié)果，自動地調(diào)節(jié)現(xiàn)時刻的濾波參數(shù),，從而達到最優(yōu)化濾波,。其中，自適應(yīng)濾波算法包括線性自適應(yīng)算法和非線性自適應(yīng)算法,，非線性自適應(yīng)算法具有更強的信號處理能力,，但計算比較復(fù)雜，實際應(yīng)用最多的仍然是線性自適應(yīng)濾波算法,。線性自適應(yīng)濾波算法的種類很多,，其中最小均方（Least Mean Square，LMS）算法和遞歸最小二乘（Recursive Least Square,，RLS）算法比較典型,，當研究中的信號是平穩(wěn)隨機信號時，采用LMS算法效果明顯,。而海雜波是非平穩(wěn)信號,，所以LMS算法很難自適應(yīng)地跟蹤統(tǒng)計特性變化的雜波干擾，因而其收斂效果一般,。而基于RLS算法自適應(yīng)濾波器克服了上述缺點,，在非平穩(wěn)環(huán)境下可以取得較滿意的效果[6]。而由于雷達雜波信號具有非平穩(wěn)特性,，所以本設(shè)計采用RLS自適應(yīng)濾波算法,。在實驗中，自適應(yīng)濾波器的階數(shù)為32,，λ為0.98,。

　　1.4 海雜波抑制模型

　　參考文獻[7]指出,，雷達信號小波變換的細節(jié)部分（高頻部分）表征的是雷達雜波的方差特性，更能表現(xiàn)出雜波的浮動特性,。所以,，對信號進行小波分解，將分解后含有目標的雜波中的高頻部分提取出來,，作為自適應(yīng)雜波對消器參考信道的輸入,，對其進行自適應(yīng)濾波。最終,，濾波器的輸出結(jié)果即抑制雜波后的目標,。雜波抑制模型如圖3所示[8]。

2 海雜波的仿真及抑制

　　2.1 海雜波仿真

　　在仿真實驗中,，分別對服從瑞利分布的雜波和服從K分布的雜波進行抑制,。首先，對這兩種分布的雜波進行仿真,，如圖4所示,。

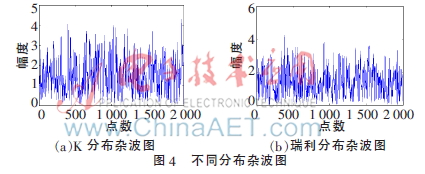
　　假設(shè)存在三個點目標，位置分別出現(xiàn)在500,，1 000,，1 700處，幅度均為3,，如圖5所示。將其加入仿真的雜波中,，如圖6所示[9],。

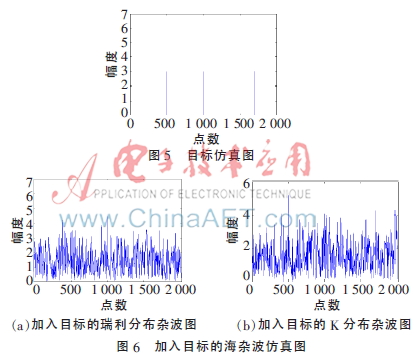
　　2.2 不同小波基雜波抑制效果比較

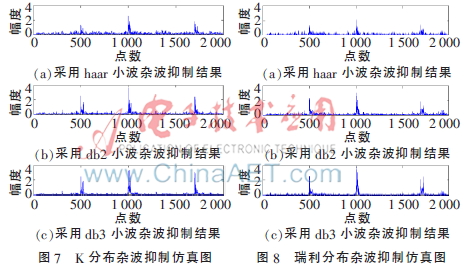
　　實驗中分別采用haar、db2和db3小波,。分別對K分布雜波和瑞利分布雜波進行抑制,，結(jié)果如圖7、圖8所示[9],。通過對比可以看出,，采用db2和db3小波的雜波抑制效果要優(yōu)于haar小波。采用db2和db3小波來處理雜波并通過自適應(yīng)濾波器都可以對雜波進行有效抑制,，并可以準確檢測出目標信號,，只不過檢測出目標信號的幅度稍有不同。同時此種方法同時適用于K分布和瑞利分布兩種雜波,。

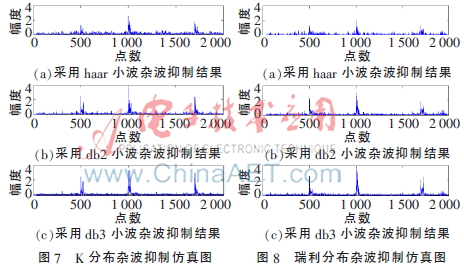
　　這說明小波分解出的細節(jié)部分（高頻部分）可以大概表征雜波特性,。同時在自適應(yīng)雜波對消器中，采用的是RLS自適應(yīng)濾波算法,，這種算法適用于非平穩(wěn)信號,，而雜波信號就是非平穩(wěn)信號,。所以，通過小波分解與自適應(yīng)雜波對消器的結(jié)合可以有效抑制雜波,，檢測出目標[10],。

　　2.3 尺度的選擇

　　以db3小波為例，分別對尺度1,、2,、3下的雜波抑制效果進行比較。圖9和圖10給出了自適應(yīng)雜波對消算法db3小波在尺度1,、2,、3下的雜波抑制效果圖。

　　從圖中可以看出,，無論是K分布雜波還是瑞利分布雜波,，在尺度為1時的雜波抑制效果是最好的。而當分解尺度大于3時,，雖然雜波可以被有效抑制,，但是目標也同時被抑制[11]。

3 結(jié)論

　　本文提出了一種將小波分解與自適應(yīng)濾波結(jié)合來抑制海雜波的方法,。通過對采用不同的小波基與不同尺度的結(jié)果進行對比分析得出,，使用db3小波和1尺度可以得到很好的效果。結(jié)果表明,，該方法能夠有效抑制海雜波并且識別出目標,。

　　參考文獻

　　[1] 湯成霞，徐曉群,，張榮濤,，等.雷達雜波抑制的新方法研究[J].現(xiàn)代雷達，2012,，34（9）：63-65.

　　[2] HAYKIN S.自適應(yīng)濾波器原理[M].北京：電子工業(yè)出版社,，2003.

　　[3] 吳永勝.小波變換在雷達信號處理中的應(yīng)用[J].通信電源技術(shù)，2013,，30（5）：84-89.

　　[4] 吳明,，肖高清，王衛(wèi)強,，等.基于小波分解的自適應(yīng)濾波算法及其應(yīng)用[J].計算機仿真,，2006，23（1）：105-107.

　　[5] 孫長生.VTS雷達雜波處理器的研究與設(shè)計[D].大連：大連海事大學(xué),，2005.

　　[6] 廖暢,，山拜·達拉拜.基于自適應(yīng)濾波的多模噪聲抑制研究[J].計算機仿真，2012,，29（4）：189-192.

　　[7] REYES J A T. DSP-based oversampling adaptive noise canceller for background noise reduction for mobile phones[J].Electrical Communications and Computers,，2012,，5（30）：327-332.

　　[8] 柳曉鳴.子波變換用于VTS雷達雜波抑制的研究[D].大連：大連海事大學(xué)，1999.

　　[9] 朱洪俊.非平穩(wěn)信號自適應(yīng)濾波的小波模型與濾波方法[J].機械工程學(xué)報,，2006,，42（8）：201-204.

　　[10] 陳鯤，陳云秋,，陳世友.海雜波建模與仿真[J].艦船電子工程,，2009，29（2）：95-98.

　　[11] 蘇昭斌,，陳紅衛(wèi).海雜波復(fù)合K分布模型的參數(shù)估計[J].計算機應(yīng)用與軟件,，2014，31（8）：273-275.