馬亞男,，戴爾晗,，陳誠

　　（南京郵電大學(xué) 自動化學(xué)院,，江蘇 南京 210023）

       摘要：在多周期結(jié)構(gòu)分析中,，最大重疊離散小波變換得到的信號周期具有明顯的局限性。在對比小波方差分析中,，提出了用最大重疊離散小波包方差法分析不同尺度小波方差圖,、功率譜，從而得到信號周期估計的最大值,。實驗結(jié)果表明,，對信號或時間序列周期結(jié)構(gòu)的分析是一種有效的方法，該方法可以準(zhǔn)確估計多周期信號的小波包方差,。

　　關(guān)鍵詞：功率譜,；多周期；小波方差,；小波包方差

　　中圖分類號：TP216+.1文獻標(biāo)識碼：ADOI： 10.19358/j.issn.1674-7720.2017.03.024

　　引用格式：馬亞男,，戴爾晗，陳誠.多周期信號的小波包方差分析方法［J］.微型機與應(yīng)用,，2017,36（3）：82-84.

0引言

　　高分辨譜估計是信號處理中的一個熱點問題,。一個信號的周期性結(jié)構(gòu)，在光譜分析中有兩種方法：FFT譜估計方法和現(xiàn)代譜估計方法,。傳統(tǒng)的傅里葉變換方法只適用于平穩(wěn)信號分析,，其分辨率是固定的。當(dāng)數(shù)據(jù)長度較短時,，分辨率較低,，且不能同時對高頻信號進行分析。所以,，在應(yīng)用程序中有很大的局限性［1］,。近年來，一些研究人員提出了基于小波變換的現(xiàn)代譜估計方法,，對頻率分辨率和估計精度有了較大的提高［23］,。這些方法已逐漸被應(yīng)用于金融、氣象,、水印,、海洋、機械,、醫(yī)療和電子信號處理領(lǐng)域［46］,。信號周期旋轉(zhuǎn)后,，功率譜的周期結(jié)構(gòu)發(fā)生變化［78］，因此,，離散小波變換不能直接用于信號的周期結(jié)構(gòu)分析,。

　　本文將基于MODWT小波方差有效地分析估計信號的頻譜，從而分析信號的周期結(jié)構(gòu),。DWT和MODWT有良好的低頻頻率分辨率,但有較低的高頻頻率分辨率,；自然極大重疊離散小波包變換(MODWPT)被認(rèn)為具有更好的頻率分辨率，高頻率可取代MODWT,。由于小波系數(shù)的突出優(yōu)勢和MODWT的縮放系數(shù)滿足平移不變性,、各分解層保持相同的分辨率和無相位失真，MODWPT非常適合于非平穩(wěn)信號處理［9］,。實驗結(jié)果表明,，使用基于MODWPT的方法來仿真信號的周期性結(jié)構(gòu)具有良好的效果。

1小波方差法

　　1.1小波方差的定義

　　給定一個離散時間信號{Xt},，它可以看作是一個實現(xiàn){Xt}的X0,X1,X2...XN-1的均值為零的平穩(wěn)過程,，且{Xt}的第d階向后差分是平穩(wěn)過程。用{j,l:l=0,1,2...Lj－1}來表示一個系數(shù)為第j階MODWT的小波濾波器,，并使得：

　　其中式（1）表示用{j,l},、{Xt}的小波濾波器濾波得到的隨機過程。

　　{Xt}基于尺度τj=2j－1的小波方差定義如下：

　　v2(τj)=var{Wj,t}（2）

　　1.2小波方差估計

　　為了估計小波方差v2x(τj),，使用寬度為L≥2d的小波濾波器,。假設(shè)L足夠大,則E{Wj,t}= 0。根據(jù)這種假設(shè)有：

　　v2(τj)=var{Wj,t}=E{(Wj,t－Wj,t)2}=E{W2j,t}（3）

　　所以小波方差的估計可以基于平方過程{W2j,t},，假設(shè)序列{xt}的樣本大小滿足N≥Lj,，并且計算出的小波系數(shù)為Wj,t，t=0,1,...,，N－1,。Wj,t，t=0,1,...,，N－1,，表示vx2(τj)的無偏估計。且小波方差的無偏估計為：

　　v

　　其中Mj=N－Lj+1,，且Lj是第j階等效小波或縮放濾波器的寬度,。

2小波包方差法

　　給定一個離散信號，零均值平穩(wěn)過程{Xt}的實值部分的序列為X0,，X1,，...XN-1，{v2j,n}的估計量為：

　　其中，n=0,1,...,2j－1且Lj=(2j－1)(L－1)+1,。然而,，如果E{xt}是未知的，過濾器{l}的性質(zhì)為∑ll=0,，{v2j,n}合適的估計量是：

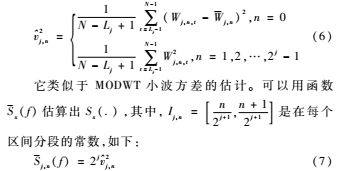
　　其中，n=0,1,...,，2j－1,，{2j,n}是小波方差估計。在低頻和高頻域中式（5）和式（6）可以估計小波方差,。與小波方差相比較,，可以得出這樣的結(jié)論：基于小波包方差的方法可以更準(zhǔn)確地進行周期性結(jié)構(gòu)分析。

3基于小波包方差周期結(jié)構(gòu)分析

　　下面有5個正弦周期模擬信號：

　　xt=sin(2×100πt)+sin(2×175πt)+sin(2×200πt)+sin(2×300πt)+sin(2×320πt)（8）

　　頻率分別為f1=100 Hz,，f2=175 Hz,，f3=200 Hz，f4=300 Hz,，f5=320 Hz,。周期分別為T1=0.01 s，T2=0.005 7 s,，T3=0.005 s,，T4=0.003 3 s，T5=0.003 1 s,。采樣周期為0.001 s,，采樣點的數(shù)量是1 000。因此,，該信號可以看作是一個離散時間序列,。

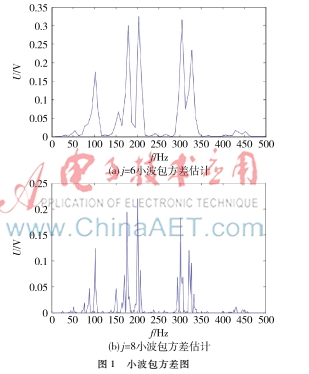
　　式（8）中,xt是在MODWPT基礎(chǔ)上在τ8=28Δt=0.256 s的尺度下由db4小波分解了6層和8層進行小波方差的估計。計算出頻率對應(yīng)于不同尺度的小波包的頻率區(qū)間,?；贛ODWPT的小波包方差圖如圖1(a)和(b)所示。圖1(a)表示尺度為0.064 s的小波方差,。圖1(b)表示尺度為0.256 s的小波方差,。

　　從圖1可以看到，小波方差圖可以分為5大峰,，其頻率大致為100 Hz,、175 Hz、200 Hz,、300 Hz和320 Hz,。下一個峰值發(fā)生在最大峰值處。從圖1可以得出結(jié)論：分解層數(shù)增加，泄漏更嚴(yán)重,。

　　通過使用方程（8）,，可以在其中估計xt的譜密度函數(shù)x(f)，結(jié)果如圖2所示,。該圖還顯示出估計是基于db4小波濾波器和分解水平j(luò)=6,，j=8。此處x(f)是分段常數(shù),。從圖2中可以看出,，分解尺度越大，分段常數(shù)區(qū)間越小,，顯示的頻率范圍越小,，峰值變尖，峰值位置越接近信號的主頻,。因此,，基于小波包方差功率譜估計可以準(zhǔn)確估計信號的多周期結(jié)構(gòu)。

　　有一個高頻信號如下：

　　xt=sin(2×20 000πt)+sin(2×20 500πt)（9）

　　根據(jù)MODWPT采樣周期是0.000 01 s和采樣點的數(shù)量為10 000,，信號被分解為10個等級,，小波包方差如圖3所示，實際尺度為τj=210Δt=0.010 24 s,。對應(yīng)的兩大峰值的頻率分別為f1≈20 000 Hz,f2≈20 500 Hz,。因此，小波包方差的方法可以有效地識別高頻信號周期結(jié)構(gòu),。

　　當(dāng)尺度較大時,，觀測范圍內(nèi)的時間軸也較大。例如,，一個低頻信號如下：

　　xt=sin(2×0.4πt)+sin(2×0.5πt)+sin(2×0.6πt)（10）

　　采樣周期為0.5 s,，采樣點的數(shù)量是2 000。在MODWPT基礎(chǔ)上信號可以分解為5層,，其中實際尺度τj=16 s,，小波包方差圖如圖4所示。三大峰對應(yīng)的頻率分別為f1≈0.4 Hz,f2≈0.5 Hz,f3≈0.6 Hz,。它表明,，小波包方差的方法可以有效地識別低頻信號周期結(jié)構(gòu)。

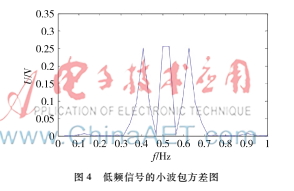
　　基于MODWPT分析信號的小波包的變異時,，理論上可以在低頻或高頻獲得高分辨率,。但是由于小波變換的特殊性，當(dāng)尺度因子減小時,，小波包的時域波形變小,，這相當(dāng)于頻率域的波形變寬,，意味著帶通濾波器更寬。如果減少了步長因子,，小波包方差圖不理想,，原因是衰減很慢，并伴隨著泄漏,。

4結(jié)論

　　使用基于MODWT或MODWPT時間信號的多尺度分析可以避免初始點和信號長度的影響,，而且還可以以不同的頻率有效地分解方差的序列?；贛ODWT方法僅在低頻分析小波方差時有效,，所以準(zhǔn)確性估計的程度是有限的。信號的低頻和高頻域可以分別基于MODWPT被分解,，因此可以得到比MODWT更高的分辨率,。這表明,，小波包方差法能更準(zhǔn)確地估計多周期結(jié)構(gòu),。此外，也可以在噪聲信號的多周期結(jié)構(gòu)分析中使用基于小波包方差的方法,。仿真結(jié)果表明,，通過MODWPT分析小波包方差和功率譜，信號周期的頻率可以有效地估計,。它提供了一種信號或序列的周期性結(jié)構(gòu)分析的有效方法,。

參考文獻

　　［1］ HERLEY C, VETTERLI M. Wavelets and recursivefilter banks［J］. IEEE Transactions on Signal Processing, 2013,41(8): 2536-2556 .

　?。?］ 李芬華,，潘立冬，常鐵原,，等.精密頻譜分析系統(tǒng)的設(shè)計與實現(xiàn)［J］. 電力自動化設(shè)備,2002,22(12):40-43.

　?。?］ 張瑛，牟龍華,，劉軍.電力系統(tǒng)頻率測量及跟蹤［J］. 電力系統(tǒng)及其自動化學(xué)報,，2003,15(3) :35-36.

　　［4］ AGHAZADEH R,LESANI H,SANAYEPASAND M,et al.New technique for frequency and amplitude estimation of power system signals［J］. IET Proceedings of Gener. Transm. Distrib.,2005,152(3) :435-440.

　?。?］ NEWLAND D E. Ridge and phase indetification in the frequency analysis of transient signals by harmonIc wavelets［J］ .Journal of Vibration and Acoustics, 1999,121(2):149-155 .

　?。?］ SHERLOCK B G,KAKAD Y P. Windowed discrete cosine and sine transforms for shifting data［J］.Signal Processing,2001,81(7): 1465-1478 .

　　［7］ 胡蔦慶,溫熙森,，陳敏.隨機共振原理在強噪聲背景信號檢測中的應(yīng)用［J］.國防科技大學(xué)學(xué)報,2001,23(4): 40-44 .

　?。?］ Wang Guanyu. The application of chaoticoscillator stoweak signal detection［J］ . IEEE Transactions on Industrial Electronics,2001,46(2): 440-444 .

　　［9］ 李一兵,，岳欣,，楊莘元．多重自相關(guān)函數(shù)在微弱正弦信號檢測中的應(yīng)用［J］.哈爾濱工程大學(xué)學(xué)報，2004，25(4):525-528.