張江波
(河北工程大學(xué) 信息與電氣工程學(xué)院,河北 邯鄲 056038)
摘要:為了提高在密集多徑信道下信號檢測性能,提出了一種基于稀疏表示的非相干檢測方法。此方法考慮了稀疏表示的原理及特點, 以稀疏信號分解、主成分分析及特征信號提取為基礎(chǔ), 通過利用假設(shè)檢驗方法對信號進行最終判決, 實現(xiàn)了在密集多徑環(huán)境下的信號檢測。仿真驗證了所提方案的可行性,對比了傳統(tǒng)方案和所提方案的檢測性能,結(jié)果表明該方法具有更好的檢測能力。
關(guān)鍵詞:信號檢測;稀疏表示;非相干檢測;密集多徑信道
中圖分類號:TN914文獻標識碼:ADOI: 10.19358/j.issn.1674-7720.2017.02.020
引用格式:張江波.基于稀疏表示的密集多徑非相干信號檢測方法研究[J].微型機與應(yīng)用,2017,36(2):66-69.
0引言
隨著通信技術(shù)的發(fā)展,未來無線通信技術(shù)不斷向著高速傳輸方向邁進,移動通信網(wǎng)絡(luò)標準逐漸邁向5G時代。在5G待選通信技術(shù)中,毫米波通信技術(shù)可能成為下一代移動通信的關(guān)鍵技術(shù)。其傳輸帶寬由低頻段增至高頻段,大帶寬具有擴頻增益、降低信號輻射等優(yōu)點,可以為大規(guī)模無線傳感器網(wǎng)絡(luò)、體域網(wǎng)、個域網(wǎng)等提供低功耗、綠色通信的解決方法,對未來無線網(wǎng)絡(luò)的發(fā)展具有重要意義[1]。
在毫米波通信技術(shù)中,典型的應(yīng)用場景常常是在室內(nèi)完成,然而,當無線傳輸系統(tǒng)帶寬超過500 MHz時,這種無線信號將呈現(xiàn)密集多徑特性。由于室內(nèi)存在著大量反射體,這種密集多徑信號將非常復(fù)雜,給信號接收機的設(shè)計帶來諸多難題。在傳統(tǒng)的窄帶/寬帶系統(tǒng)中,通常包含3~10個多徑信號,一般可以通過信道估計、Rake接收機進行信號處理[2],通過有效的分集增益減小多徑帶來的損耗,提高系統(tǒng)的性能。但是,在毫米波大帶寬、密集多徑的情況下,路徑多達幾十條至上百條。多徑數(shù)量的急劇增加,使得接收機的采樣頻率高達數(shù)兆赫茲,大大增加了數(shù)模采樣的功耗和對器件的要求,其相應(yīng)的信道估計算法的復(fù)雜度也極高。此外,由于Rake接收機需要采用大量接收抽頭進行合并,這種情況使得信號接收機的系統(tǒng)異常復(fù)雜,硬件要求極高而難以實現(xiàn)。
為了克服上述問題,文獻[3]提出了簡化密集多徑信道下的帶寬信號檢測過程(TransmittedReference, T-R)的方案, 這種方案將第一個信號作為傳送模板,在相鄰的第二個信號上加載有用信息,然后對這兩個信號做信號相關(guān)處理,實現(xiàn)了信道的有效估計和Rake接收。該方案雖然降低了密集多徑下接收機的復(fù)雜度,但是犧牲了一半的傳輸效率。
近幾年,在密集多徑信道下的非相干檢測[45](NonCoherent Detection, NCD)得到了廣泛關(guān)注,其代表技術(shù)是能量檢測[67](Energy Detector,ED)。能量檢測具有許多優(yōu)勢,例如無需進行信道估計,避免Rake接收結(jié)構(gòu),顯著降低了對通信系統(tǒng)同步的要求等。這些優(yōu)點為進一步降低無線通信系統(tǒng)復(fù)雜性以及為密集多徑大帶寬通信技術(shù)的發(fā)展提供了可行方案。然而,現(xiàn)有的非相干能量檢測技術(shù)受到噪聲和環(huán)境影響較為嚴重,其檢測性能有待進一步提高。
信號稀疏表示理論由于其獨特的魅力成為近20年來信號處理界一個非常引人關(guān)注的研究熱點[8]。信號稀疏表示可以使得信號獲得更為簡潔的表達方式,從而使信號中所蘊含的信息更容易地表現(xiàn)出來,更方便進一步對信號進行加工處理[9]。本文針對現(xiàn)有能量檢測的特征,提出一種基于稀疏信號處理的信號檢測方案,用以提高非相干檢測機制的性能。本文首先介紹了稀疏表示的原理,隨后給出基于稀疏表示的稀疏信號分解、主成分分析及特征信號提取,最后利用假設(shè)檢驗方法對信號進行最終判決。為驗證所提方案的可行性及有效性,本文通過仿真實驗對比了傳統(tǒng)方案與所提的方法,結(jié)果表明本文所提方案的檢測能力更優(yōu)秀。
1稀疏表示
稀疏表示[10]是指在某種變換或冗余完備字典上用盡可能少的測量值來表征原始信號。假設(shè)一個超完備冗余字典為D=[d1,…,dn],輸入信號集合為y∈Rm,這個輸入信號可以被重新表示為D與稀疏系數(shù)矩陣x=[x1,…,xn]T的一種稀疏線性組合,表達式為

這里,x即為輸入信號y的稀疏表示系數(shù)。
稀疏表示的問題在于尋找n×1個最少非零系數(shù)x來表示y。這個問題常常使用求解一個優(yōu)化問題,即0范數(shù)問題:
minx0s.t.y=Dx(2)
其中,0代表0范式,它的作用在于標記非零項個數(shù)。
更進一步,這個優(yōu)化問題還可以等價于一個在1范式情況下的凸優(yōu)化問題,模型如下:
minx1s.t.y=Dx(3)
其中,1代表1范式。
有許多算法可以求解這個優(yōu)化問題,例如梯度投影算法[11]、貪婪算法[12]等。這里,本文使用的求解算法為正交匹配追蹤(Orthogonal Match Pursuit,OMP)算法[13]。
2稀疏信號處理
根據(jù)稀疏表示原理,將原始脈沖信號在超完備字典下進行稀疏分解。在這一過程中,選擇合適的超完備字典是非常重要的過程,因為這一過程不僅影響信號稀疏表示的稀疏性,還影響有用信號特征的選擇。針對密集多徑的信號特點,標準的多分辨字典是一種較為有效的選擇,例如基于小波理論的字典。這些字典已經(jīng)在已有的文獻中用來處理自然場景圖像,并且有較好的表現(xiàn)[14]。由小波函數(shù)ψ(t)及其擴展函數(shù)φ(t)經(jīng)過平移伸縮以及尺度縮放,最終形成小波冗余字典:
ψj,k(t)=2-j/2ψ(2-jt-k)
φj,k(t)=2-j/2φ(2-jt-k) (4)
這里使用Symletes小波字典作為過完備冗余字典[15]。
依據(jù)公式(1)和(3),并且基于選定的過完備冗余字典,可以獲取稀疏表示系數(shù)來重新表示原始的接收信號,也就是說,利用OMP算法和小波字典,接收信號可以被分解為稀疏系數(shù)。在這一過程中,原始的接收信號被轉(zhuǎn)換為稀疏分解系數(shù),而這些系數(shù)保留了原始信號特征成為進一步處理的對象。
通常,字典包含的原子數(shù)目大于接收信號數(shù)目,為了避免高維系數(shù)集的出現(xiàn),有必要利用特征提取進行降維。本文使用主成分分析算法進行降維。
假設(shè)輸入的稀疏系數(shù)為p=[p1,...,pn],想轉(zhuǎn)換這些系數(shù)到一個更低的維度向量pV=[p1,...,pv],這一問題可以被表示為:
pV=E(p-μp)(5)
其中,pV是主成分分析系數(shù),它可以以一種低維形式表示原始的稀疏系數(shù)向量。E包含協(xié)方差矩陣p中v個最大的特征值所對應(yīng)的向量,而μp表示樣本均值。
隨后,利用這些經(jīng)過稀疏表示以及主成分分析的系數(shù)集合,提取三個量化特征用以區(qū)分信號的不同特征,第一個特征為能量集中度:
![UY]2V~Y%I@LME60RU~NJCMO.png UY]2V~Y%I@LME60RU~NJCMO.png](http://files.chinaaet.com/images/2017/03/13/6362503801801760781652610.png)
3基于假設(shè)檢驗的信號檢測
二元假設(shè)檢驗是信號檢測中常用的策略,本文根據(jù)信號統(tǒng)計特性構(gòu)建相對應(yīng)的假設(shè)檢驗形式。二元假設(shè)檢驗是通過測量一組給定的假設(shè)狀態(tài)來判定是否為所需信號:
Ho: 零假設(shè)
H1: 其他
存在兩種類型的錯誤:虛假警報PFA(當H1被確定,但真實值為Ho時)以及漏檢(當Ho被確定,但真實值為H1時),這里常用檢測概率PD表示漏檢的補集。
對于虛假警報PFA和檢測概率PD,可以利用Neyman-Pearson定理[16]獲取。當信號被接收者獲取后,通過一些處理,其統(tǒng)計信號可以表示為:
f(τ)=(τ)+σ2(10)
其中,σ2是噪聲方差。
這種情況下,假設(shè)f(τ)是服從高斯分布的統(tǒng)計特征,參考特征為f′(τ),從而得:
H0:f(τ)-f′(τ)=σ2
H1:f(τ)-f′(τ)=S+σ2 (11)
其中,S是區(qū)分與σ2的變量。
然后根據(jù)變量的統(tǒng)計特性分析和相應(yīng)的統(tǒng)計信號檢測,可以計算出目標特征的概率密度函數(shù)。通過預(yù)先設(shè)置虛警概率,可以計算獲得檢測概率和實際的虛警概率。這種條件下概率密度函數(shù)為:

其中ξ表示為PFA的閾值。
根據(jù)NeymanPearson定理,計算實際的虛警概率和檢測概率分別為:

4數(shù)值仿真
在低復(fù)雜度非相干檢測框架內(nèi),需要將信號調(diào)制方式考慮在內(nèi)。由于非相干檢測中不對信道沖激響應(yīng)進行估計,相位調(diào)制方式將不適用,因而不采用移相鍵控(PSK)等相位調(diào)制。本文采用調(diào)時脈沖位置調(diào)制(THPPM),調(diào)制通過跳時機制實現(xiàn)時間多址接入,其調(diào)制信號可表示為:
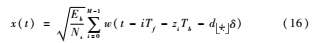
其中Tb表示單比特持續(xù)時間,Tf為幀時間長度,zi 為偽隨機調(diào)時序列,δ為符號中比特間隔。
本文仿真采用IEEE 802.15.3a Task Group (TG)規(guī)定的SV多徑信道模型。圖1所示為典型視距傳輸距離為1~4 m通信場景下密集多徑信道沖激響應(yīng)。

圖2表示在假設(shè)檢驗情況下稀疏信號處理過程,H0下僅包含加性白噪聲,而H1下同時包含噪聲和多徑接收信號。從圖中可以看出,兩類信號在實域采集后的原始信號非常接近,而經(jīng)過稀疏表示處理之后特征信息已經(jīng)表現(xiàn)出來,但是特征空間相對較大,經(jīng)過主成分分析后(PCA),相關(guān)的參數(shù)空間明顯變少,而且特征信息依舊保留。因此,通過稀疏信號處理可以表征出這兩類信號的不同,從而為信號的檢測提供了特征信息。
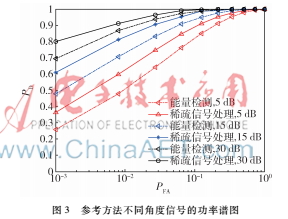
圖3參考方法不同角度信號的功率譜圖圖3表示在經(jīng)過假設(shè)檢驗后,本文所提方法與傳統(tǒng)的能量檢測方法性能相對比。實驗分別從信噪比(SNR)為5 dB、15 dB、30 dB由低到高開展。從圖中可以清楚地看到,隨著信噪比的升高,兩種方案的檢測性能也有所提升,而且,在對虛警概率PFA的限制條件逐步放寬的前提下,檢測性能PD逐漸趨近于1,這也是NP檢測的特點所在,即在給定虛警概率的條件下,檢測概率達到最好。從圖中可以看出,無論是在哪種信噪比條件下,所提的基于稀疏信號處理的信號檢測方法都比傳統(tǒng)的能量檢測方法性能優(yōu)秀,這也說明了本文所提方法的有效性。
5結(jié)論
本文對密集多徑信道下非相干信號檢測方法進行了研究,為進一步提高非相干信號檢測的性能,提出了一種基于稀疏表示的稀疏信號處理方案。本文構(gòu)建了以稀疏表示為基礎(chǔ)的特征信號,將假設(shè)檢測方案作為最終的信號檢測判決。仿真表明所提出的方法具有可行性,其檢測性能要優(yōu)于傳統(tǒng)的能量檢測方案。
參考文獻
[1] Yang Liuqing, GIANNAKIS G B. Ultrawideband communications: an idea whose time has come [J]. IEEE Signal Processing Magazine, 2004, 21(6): 26-54.
[2] CASSIOLI D, WIN M Z, VATALARO F, et al. Low complexity rake receivers in ultrawideband channels [J]. IEEE Transactions on Wireless Communications,2007,6(4): 1265-1275.
[3] FRANZ S, MITRA U. Generalized UWB transmitted reference systems [J]. IEEE Journal on Selected Areas in Communications, 2006, 24(4): 780-786.
[4] GERALD J B, FERNANDES J R, CAEIRO P. Ultrawideband noncoherent transceivers[R]. Research Report, INESCID, Lisboa, 2010.
[5] BENAMOR I, TALL N, DEHAESE N, et al. A fully differential 7.28.5 GHz LNA for a self synchronized and dutycycled UWB OOK receiver[C]. 2015 IEEE International Conference on Ubiquitous Wireless Broadband (ICUWB), IEEE, 2015: 1-5.
[6] 陳長興, 符輝, 牛德智,等. 基于雙門限能量檢測的協(xié)作頻譜感知算法[J]. 系統(tǒng)工程與電子技術(shù), 2013, 35(8):1742-1746.
[7] 張學(xué)軍, 嚴金童, 田峰,等. 基于差分能量檢測的雙門限協(xié)作頻譜感知算法[J]. 儀器儀表學(xué)報, 2014, 35(6):1325-1330.
[8] 張鳳. 稀疏表示理論的研究及其在圖像去噪中的應(yīng)用[D]. 西安:西安電子科技大學(xué), 2014.
[9] 崔嵩. 基于稀疏信號的學(xué)習字典算法及其應(yīng)用[D]. 北京:北京工業(yè)大學(xué), 2014.
[10] GUHA T, WARD R. Learning sparse representations for human action recognition [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(8): 1576-1588.
[11] FIGUEIREDO M A T, NOWAK R D, WRIGHT S J. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems [J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 586-597.
[12] MALLAT S, Zhang Zhifeng. Matching pursuits with timefrequency dictionaries [J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415.
[13] TROPP J, GILBERT A. Signal recovery from random measurements via orthogonal matching pursuit [J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666.
[14] STARCK J L, ELAD M, DONOHO D L. Image decomposition via the combination of sparse representations and a variational approach [J]. IEEE Transactions on Image Processing, 2005, 14(10): 1570-1582.
[15] CHEN S S, DONOHO D, SAUNDERS M. Atomic decomposition by basis pursuit [J]. Society for Industrial and Applied Mathematics Review, 1998, 20(1): 33-61.
[16] KAY S M. Fundamentals of Statistical Signal Processing: Detection Theory Volume Ⅱ[M]. Prentice Hall, 2011.

