0 引言

    古代建筑圖紙能夠反映古人對(duì)建筑獨(dú)特的認(rèn)識(shí)與理解，不僅具有極高的歷史價(jià)值,、文化價(jià)值和科學(xué)價(jià)值,，同時(shí)也是現(xiàn)代仿古建筑、園林景觀和旅游景區(qū)的重要借鑒^[1],。建筑圖紙的質(zhì)地,、圖形、字體及涂料具有多樣性,，需要特別的保護(hù),。當(dāng)前,，在實(shí)際的工作環(huán)境中，大部分建筑圖紙以卷宗的形式進(jìn)行保存,，隨著時(shí)間的變遷,，建筑圖紙的缺損非常嚴(yán)重，且在掃描,、微縮處理中,，圖紙的像素丟失嚴(yán)重。對(duì)建筑圖紙進(jìn)行修復(fù),、評(píng)估及再利用,，一直作為建筑學(xué)科及計(jì)算機(jī)圖像處理等領(lǐng)域的研究熱點(diǎn)而受到關(guān)注^[2]。僛文峰等人指出圖紙的破損主要是由于圖紙質(zhì)地的酸性化而變黃,、發(fā)干, 以及隨之而來(lái)的粉碎和撕毀情況比較嚴(yán)重,；由于時(shí)間久遠(yuǎn)，圖紙質(zhì)地及顏料也會(huì)出現(xiàn)不同程度的缺損,、黃色斑點(diǎn)等破損,；在對(duì)古建筑圖紙進(jìn)行信息化加工的過(guò)程中也會(huì)造成像素的丟失，出現(xiàn)黑色斑點(diǎn)等,。本文針對(duì)掃描及微縮以后的古建筑圖像提出一種新的基于字典學(xué)習(xí)的修復(fù)方法,，該算法在稀疏域針對(duì)污損圖像的特迭代處理，從而達(dá)到古建筑圖紙修復(fù)的目的,。通過(guò)實(shí)驗(yàn)表明,，該算法能較好地修復(fù)古建筑圖像，降低了圖像的均方誤差,，在實(shí)際應(yīng)用中具有良好的前景,。

1 古建筑圖像修復(fù)模型

1.1 基于稀疏表示的古建筑圖像處理模型

    在圖像處理領(lǐng)域^[3]，任一理想的古建筑圖像可以表示為y₀∈R^N,，稀疏表示的目標(biāo)是找到一個(gè)稀疏表示向量x₀,，且x₀的0范數(shù)||x₀||₀=k₀，滿足：y₀=Ax₀,。A為字典,，B為圖像退化算子，表示圖像丟失掉的p個(gè)采樣,，則：y=By₀,。B表示單位矩陣(大小為：n×n)根據(jù)丟失掉的（缺損）采樣去除p行后的矩陣，其大小為(n-p)×n,，則古建筑圖像修復(fù)問(wèn)題就轉(zhuǎn)化為求其稀疏表示向量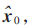進(jìn)而獲得未降質(zhì)圖像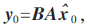則可以建模為式(1)^[4]：

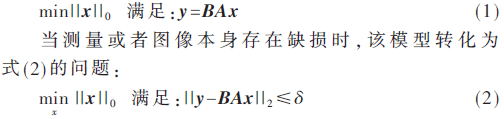
1.2 對(duì)模型的求解

    該問(wèn)題中由于原始古建筑圖像y₀未知,，且古建筑圖像一般較大，存在多種類型的缺損，因此需要對(duì)大的圖像進(jìn)行分塊,。根據(jù)給定的字典A,，將大的圖像分割成一些小的塊后，每個(gè)塊都有其稀疏表示系數(shù),，降質(zhì)操作B為一矩陣,，根據(jù)Elad等人的原理，該問(wèn)題屬于M-稀疏域模型,，則可以轉(zhuǎn)化如下最大后驗(yàn)概率問(wèn)題^[5]：

    下一部分獲得該模型中字典A的求解，通過(guò)式(5)能夠獲得輸出圖像,，對(duì)丟失掉的像素,，通過(guò)塊中已知像素進(jìn)行平均獲得。

2 字典學(xué)習(xí)算法

    字典學(xué)習(xí)過(guò)程一般分為2個(gè)階段,，分別是稀疏編碼及字典更新,。在對(duì)式(5)求解時(shí)，一般假設(shè)字典A∈R^n×k(k>n)為已知,，如DCT,、DWT和FFT等。為了進(jìn)一步提高修復(fù)古建筑圖像的修復(fù)能力,，本文分別通過(guò)MOD算法和K-SVD算法進(jìn)行字典學(xué)習(xí),，在字典學(xué)習(xí)過(guò)程中需考慮缺損像素。因此,，一旦獲得字典,，就可以完成稀疏編碼，然后固定系數(shù),，再更新字典,，從而轉(zhuǎn)化為求式(6)錯(cuò)誤的最小值：

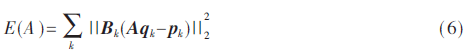
2.1 MOD字典學(xué)習(xí)算法

    MOD算法（Method of Optimal Direction）也稱為最優(yōu)方向法^[6]，該算法由K.Engan等人在1999年提出,通過(guò)對(duì)錯(cuò)誤求導(dǎo),，然后令其為0,，則可得：

2.2 改進(jìn)的K-SVD字典學(xué)習(xí)算法

    本文根據(jù)缺損的古建筑圖像進(jìn)行K-SVD字典學(xué)習(xí)，利用K-SVD算法[7]每次更新字典A的一列,，對(duì)字典的第j列a_j,，根據(jù)式(6)，僅有第k塊用到了這個(gè)原子,，將其表示為域P_k,，則可將式(6)進(jìn)行如下轉(zhuǎn)化：

    將圖像塊合并后輸出即可獲得最終修復(fù)圖像，經(jīng)過(guò)字典學(xué)習(xí)后獲得的MOD字典及K-SVD字典如圖1和圖2所示,。由圖可見(jiàn),，K-SVD字典包含了缺損圖像形變區(qū)的原子，表明K-SVD字典能夠根據(jù)圖像的特點(diǎn)進(jìn)行自適應(yīng)調(diào)整,，從而保留更多的細(xì)節(jié)和邊緣信息,，更加有利于后續(xù)的處理,。

2.3 算法分析

    該算法的計(jì)算復(fù)雜度可以分為兩部分：稀疏編碼、字典更新（迭代J次）與最終的輸出過(guò)程構(gòu)成,。古建筑圖像中的每個(gè)像素點(diǎn)的計(jì)算復(fù)雜度為：O(K×L×J),，其中，K為字典的列向量的個(gè)數(shù),，L為每個(gè)系數(shù)的非零元素的個(gè)數(shù),，一般取決于古建筑圖像的噪聲的方差和缺損像素的個(gè)數(shù)。

3 模擬實(shí)驗(yàn)

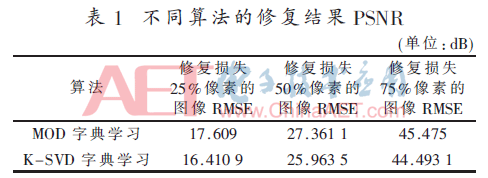
    對(duì)本文提出算法的性能進(jìn)行測(cè)試,，實(shí)驗(yàn)用古建筑圖像稱為重檐四角亭,，來(lái)源于成都理工大學(xué)；圖像的大小為256×256,。實(shí)驗(yàn)所使用的PC是CPU 3.0 GHz,，內(nèi)存為2 GB，算法用GNUOctave進(jìn)行實(shí)現(xiàn),。圖3分別為加噪20 dB后,，損失50%像素后的原始古建筑圖像，以及采用MOD字典學(xué)習(xí)算法的修復(fù)結(jié)果和采用K-SVD字典學(xué)習(xí)算法的修復(fù)結(jié)果圖,。設(shè)置字典原子的個(gè)數(shù)為256,，圖像塊大小為8×8。圖4為隨著迭代次數(shù)的增加,，MOD字典學(xué)習(xí)算法和K-SVD字典學(xué)習(xí)算法的修復(fù)效果對(duì)比圖,。表1為采用MOD字典學(xué)習(xí)算法和K-SVD字典學(xué)習(xí)算法迭代15次后所獲得的RMSE(均方根誤差)。由圖3可見(jiàn),，采用K-SVD算法修復(fù)的效果明顯優(yōu)于采用MOD算法修復(fù)的效果,，尤其是右上角塔頂處的局部放大圖所示。

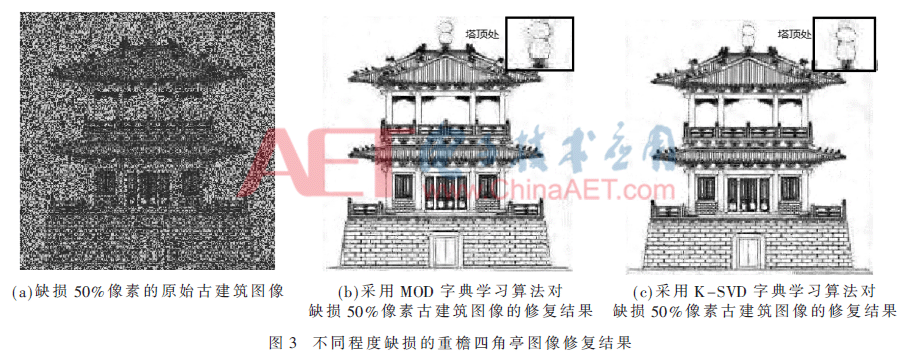
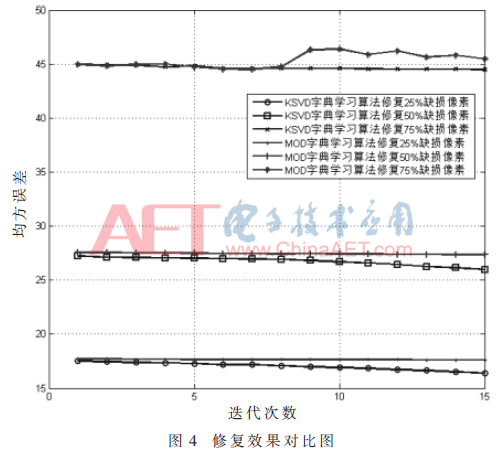
    本實(shí)驗(yàn)中運(yùn)用K-SVD字典學(xué)習(xí)算法實(shí)現(xiàn)了對(duì)古建筑圖像的修復(fù),，由圖4可見(jiàn),，K-SVD字典學(xué)習(xí)算法的修復(fù)效果優(yōu)于MOD字典學(xué)習(xí)算法，且 K-SVD算法的魯棒性更強(qiáng),。

4 結(jié)論

    本文通過(guò)對(duì)缺損古建筑圖像問(wèn)題進(jìn)行建模,，然后利用字典學(xué)習(xí)算法實(shí)現(xiàn)對(duì)缺損圖像的修復(fù)。通過(guò)對(duì)重檐四角亭古建筑圖像進(jìn)行修復(fù)試驗(yàn),，表明K-SVD字典學(xué)習(xí)算法具有更優(yōu)的效果,。本文利用機(jī)器學(xué)習(xí)及圖像處理技術(shù)對(duì)解決古建筑圖紙、古文獻(xiàn)修復(fù)等問(wèn)題提出了新的思路,，對(duì)該算法的優(yōu)化和應(yīng)用的拓展是下一步研究的重點(diǎn),。

參考文獻(xiàn)

[1] 王茹.古建筑數(shù)字化及三維建模關(guān)鍵技術(shù)研究[D].西安：西北大學(xué)，2010.

[2] 李四明.工程圖紙輸入與自動(dòng)識(shí)別系統(tǒng)的研究[D].北京：中國(guó)農(nóng)業(yè)大學(xué)，2000.

[3] N Metaxas D,，AXEL L.Recent novel methods and approaches in sparsity-based compressive sensing and sparse learning have shown promising results. Introduction[J].Med Image Anal,，2014，18(6)：819.

[4] ELDAR Y C.Compressed sensing：theory and applications[M].Cambridge University Press,，2012：556.

[5] ELAD M,，AHARON M.Image denoising via sparse and redundant representations over learned dictionaries[J].IEEE Transactions Image Process，2006,，15(12)：3736-3745.

[6] OLSHAUSEN B A,，F(xiàn)IELD D J.Sparse coding with an overcomplete basis set: a strategy employed by V1[J].Vision Research，1997,，37(23)：3311-3325.

[7] RUBINSTEIN R,，PELEG T，ELAD M.Analysis K-SVD：a dictionary-learning algorithm for the analysis sparse model[J].IEEE Transactions on Signal Processing,，2013,，61(3)：661-677.