0 引言

    相關(guān)向量機(jī)(Relevance Vector Machine,，RVM)^[1]是建立在支持向量機(jī)(Support Vector Machine,，SVM)基礎(chǔ)上的一種學(xué)習(xí)方法，依靠稀疏貝葉斯統(tǒng)計(jì)理論建立訓(xùn)練模型,。RVM與SVM相比,，函數(shù)形式相似，但RVM的核函數(shù)不需要滿(mǎn)足Mercer條件以及能提供概率式輸出使它更具優(yōu)勢(shì)^[2],。近年來(lái)RVM在回歸估計(jì),、模式識(shí)別及工程領(lǐng)域方面^[3]得到了較為廣泛的應(yīng)用，但仍存在最優(yōu)核參數(shù)不易確定的問(wèn)題,，所以部分學(xué)者將智能優(yōu)化算法應(yīng)用到RVM核參數(shù)尋優(yōu)中^[4],，取得了一定的成效。

    果蠅算法^[5](Fruit fly Optimization Algorithm,，F(xiàn)OA)是由PAN W T根據(jù)果蠅覓食的行為提出的一種智能優(yōu)化算法,。雖然該算法被廣泛應(yīng)用到各個(gè)領(lǐng)域^[6]，但在實(shí)際應(yīng)用過(guò)程中,，也存在陷入局部最優(yōu)解的情況,，文獻(xiàn)[7]提出了具有Levy飛行特征的雙子群果蠅優(yōu)化算法（LFOA），有效地解決了FOA陷入局部最優(yōu)的問(wèn)題,，提高了算法的性能,。為了提高RVM分類(lèi)器的性能，本文提出了一種基于LFOA算法的RVM核函數(shù)參數(shù)優(yōu)化方法,，并通過(guò)UCI標(biāo)準(zhǔn)數(shù)據(jù)庫(kù)的仿真實(shí)驗(yàn),，驗(yàn)證了方法的有效性和可靠性。

1 相關(guān)向量機(jī)

1.1 模型描述

    假設(shè)每個(gè)樣本獨(dú)立分布,，p(t|x)采用Bernoulli分布,，可得預(yù)測(cè)結(jié)果t的后驗(yàn)概率的似然函數(shù)為：

    根據(jù)概率預(yù)測(cè)公式，新的輸入向量x?鄢所對(duì)應(yīng)的目標(biāo)向量t?鄢求得的條件概率為：

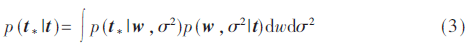
    根據(jù)稀疏Bayes理論,，給權(quán)值向量w分配獨(dú)立的零均值Gauss先驗(yàn)分布：

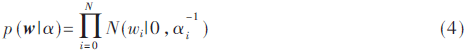
    經(jīng)過(guò)多次迭代后可發(fā)現(xiàn)大部分權(quán)值都變得很小,，只有很少一部分權(quán)值非零，根據(jù)式(1),，只有非零權(quán)值對(duì)應(yīng)的訓(xùn)練向量對(duì)目標(biāo)值起作用,，稱(chēng)為相關(guān)向量(RVs)，則RVM模型可重新表示為：

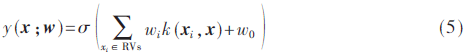
1.2 RVM多分類(lèi)

    最后,，通過(guò)式(8)累加所有分類(lèi)器的概率輸出,，并采用“最大概率贏^[9]”的策略將x_test判定為累加后驗(yàn)概率最大的類(lèi)別。

1.3 核參數(shù)對(duì)RVM分類(lèi)性能的影響

    相關(guān)向量機(jī)的核函數(shù)可將低維數(shù)據(jù)樣本映射到高維特征空間,，從而實(shí)現(xiàn)樣本的線(xiàn)性可分,，所以其參數(shù)的設(shè)置對(duì)RVM的分類(lèi)性能有著極其重要的影響。研究以比較常用,、非線(xiàn)性映射能力較強(qiáng)的徑向基核函數(shù)^[10](RBF Kernel)為例,，利用UCI數(shù)據(jù)庫(kù)中Sonar分類(lèi)數(shù)據(jù)（共208個(gè)樣本）進(jìn)行試驗(yàn)，將Sonar數(shù)據(jù)集中的全部數(shù)據(jù)作為訓(xùn)練樣本對(duì)RVM分類(lèi)模型進(jìn)行訓(xùn)練,，同時(shí)也將全部數(shù)據(jù)作為測(cè)試樣本輸入已訓(xùn)練的RVM模型中進(jìn)行學(xué)習(xí)能力測(cè)試,。核參數(shù)值與相關(guān)向量(RVs)和訓(xùn)練時(shí)間的關(guān)系如表1所示。

    根據(jù)表1可知,，隨著核函數(shù)參數(shù)逐漸增大,，相關(guān)向量的數(shù)量呈現(xiàn)逐漸下降的趨勢(shì)，不同核參數(shù)所對(duì)應(yīng)的訓(xùn)練時(shí)間不同,，為進(jìn)一步說(shuō)明核函數(shù)參數(shù)對(duì)RVM性能的影響,，圖1給出了分類(lèi)準(zhǔn)確率隨著核參數(shù)的變化趨勢(shì)。

    由圖1和表1可知,，改變核函數(shù)參數(shù)實(shí)際上是改變映射函數(shù)關(guān)系,，進(jìn)而改變數(shù)據(jù)樣本映射到高維特征空間的可區(qū)分程度，所以核參數(shù)的選取對(duì)RVM性能有較大程度的影響,，同時(shí)也只有選擇適當(dāng)?shù)暮藚?shù),，RVM的學(xué)習(xí)能力和泛化能力才能得到提升。

2 LFOA-RVM核參數(shù)優(yōu)化方法

2.1 LFOA算法

    LFOA算法是將Levy飛行特征和果蠅算法相結(jié)合,，利用Levy飛行的高度隨機(jī)性使果蠅種群容易跳出局部最優(yōu),，LFOA算法的具體步驟參見(jiàn)文獻(xiàn)[7]。

    LFOA算法在尋優(yōu)過(guò)程中,，分別計(jì)算果蠅個(gè)體與當(dāng)代最優(yōu)個(gè)體和最差個(gè)體的歐式距離Dist_best和Dist_worst,，若Dist_best<Dist_worst，則將果蠅個(gè)體劃分到較優(yōu)子群,，否則劃分為較差子群,，迭代過(guò)程中，兩個(gè)子群的果蠅個(gè)體數(shù)量是動(dòng)態(tài)變化的,。較優(yōu)子群圍繞最優(yōu)個(gè)體按式(9)進(jìn)行Levy飛行：

2.2 LFOA-RVM優(yōu)化核參數(shù)流程

    基于LFOA算法優(yōu)化RVM核參數(shù)的流程如圖2所示,，具體步驟如下：

    (1)將數(shù)據(jù)集分為訓(xùn)練樣本和測(cè)試樣本，訓(xùn)練樣本用于RVM核參數(shù)選擇和建立RVM分類(lèi)模型,，測(cè)試樣本則用于檢驗(yàn)RVM分類(lèi)器性能,；

    (2)初始化LFOA算法種群規(guī)模、迭代次數(shù),、果蠅個(gè)體起始位置和搜索距離以及Levy飛行步進(jìn)長(zhǎng)度等參數(shù),；

    (3)對(duì)訓(xùn)練樣本采用5折交叉驗(yàn)證[11](5-fold cross validation),，將交叉驗(yàn)證平均準(zhǔn)確率作為適應(yīng)度函數(shù)，選擇最大準(zhǔn)確率對(duì)應(yīng)的核參數(shù)值作為RVM分類(lèi)模型參數(shù)的設(shè)定值,；

    (4)根據(jù)果蠅個(gè)體的適應(yīng)度,，按照與最優(yōu)個(gè)體和最差個(gè)體間的歐氏距離大小將果蠅分類(lèi)，并按式(9)和式(10)進(jìn)行位置更新,；

    (5)計(jì)算新位置果蠅的適應(yīng)度,，按照規(guī)則更新全局信息；

    (6)重復(fù)步驟(4)和(5),，最終輸出最優(yōu)核參數(shù)值,。

3 仿真實(shí)驗(yàn) 

3.1 數(shù)據(jù)源與參數(shù)設(shè)置

    為了驗(yàn)證LFOA-RVM的有效性，從UCI機(jī)器學(xué)習(xí)標(biāo)準(zhǔn)數(shù)據(jù)庫(kù)中選取了4個(gè)數(shù)據(jù)集進(jìn)行仿真實(shí)驗(yàn),。算法采用MATLAB R2011b實(shí)現(xiàn),，RVM工具箱為SB2_Release_200^[12]，實(shí)驗(yàn)中使用的UCI數(shù)據(jù)集如表2所示,。

    為了便于對(duì)比,，分別利用LFOA、FOA,、遺傳算法(GA)和粒子群算法(PSO)同時(shí)對(duì)RVM的核參數(shù)進(jìn)行尋優(yōu),。將全部算法的種群規(guī)模設(shè)置為20，最大迭代次數(shù)為100,，g的搜索范圍設(shè)置為0~500,；在LFOA算法中步進(jìn)長(zhǎng)度設(shè)置為1.5；GA算法中,，交叉概率p_c=0.7,，變異概率p_m=0.1；PSO算法中局部搜索參數(shù)c₁=1.5,，全局搜索參數(shù)c₂=1.7,。

3.2 結(jié)果分析

    利用表2中的4組數(shù)據(jù)按照2.2節(jié)所述的優(yōu)化流程對(duì)LFOA-RVM性能進(jìn)行測(cè)試，尋優(yōu)迭代過(guò)程中的適應(yīng)度曲線(xiàn)如圖3所示,。

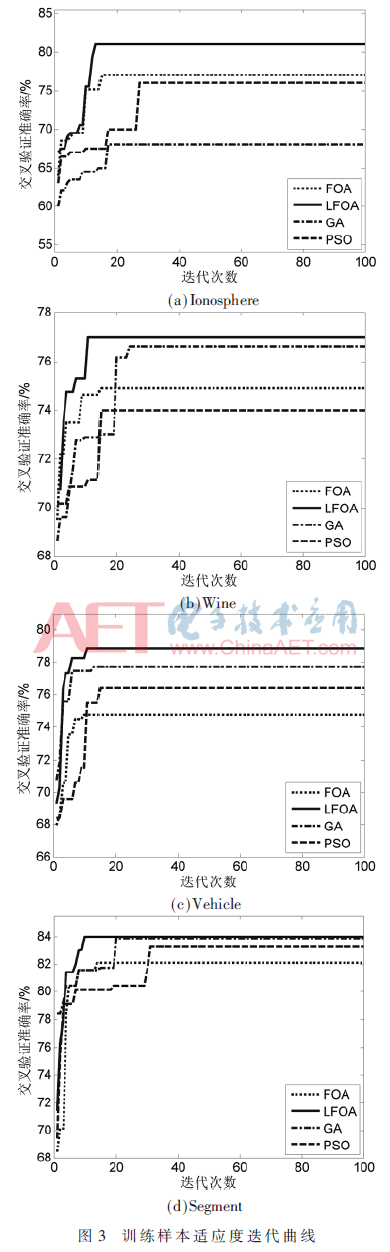
    根據(jù)圖3可知,，F(xiàn)OA、GA和PSO算法在尋優(yōu)時(shí)都不同程度的出現(xiàn)了陷入局部最優(yōu)解而無(wú)法跳出的情況,，與以上3種算法相比,，LFOA由于Levy飛行高度的隨機(jī)性從而更容易跳出局部最優(yōu)，并且適應(yīng)度更高,，尋優(yōu)速度更快,。

    4組數(shù)據(jù)集測(cè)試樣本的測(cè)試結(jié)果如表3~6所示。在表3~6中，平均準(zhǔn)確率為使用數(shù)據(jù)集進(jìn)行5次實(shí)驗(yàn)后得到的平均測(cè)試準(zhǔn)確率,；最高準(zhǔn)確率為實(shí)驗(yàn)過(guò)程中得到的最高測(cè)試準(zhǔn)確率,；最優(yōu)核參數(shù)為達(dá)到最高測(cè)試準(zhǔn)確率時(shí)RVM分類(lèi)模型核函數(shù)參數(shù)的值。

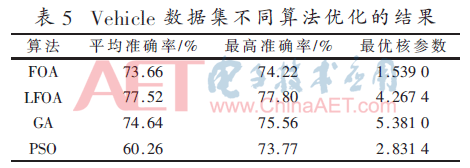
    根據(jù)測(cè)試結(jié)果可知,，LFOA-RVM不論是解決二分類(lèi)問(wèn)題或者是多分類(lèi)問(wèn)題,，都可以達(dá)到較高的測(cè)試準(zhǔn)確率，并且4組UCI數(shù)據(jù)集的最優(yōu)核參數(shù)值跨度較大,，表明了LFOA算法具備較強(qiáng)的全局搜索能力，驗(yàn)證了利用LFOA算法進(jìn)行RVM核參數(shù)尋優(yōu)的有效性,。為了便于比較各算法的尋優(yōu)穩(wěn)定性,，計(jì)算出多次實(shí)驗(yàn)的測(cè)試結(jié)果方差，如表7所示,。

    由表7可知,，Ionosphere、Wine和Segment數(shù)據(jù)集進(jìn)行多次測(cè)試,，LFOA算法所得的方差小于其他幾種算法,，Vehicle數(shù)據(jù)集中LFOA測(cè)試結(jié)果的方差雖略大于FOA，但明顯小于其他兩種算法,，表明了LFOA-RVM測(cè)試結(jié)果的波動(dòng)程度較小,，驗(yàn)證了該方法具有較高的尋優(yōu)穩(wěn)定性；LFOA結(jié)合了FOA算法局部尋優(yōu)精度高與Levy飛行容易跳出局部最優(yōu)值的優(yōu)勢(shì),，提高了全局搜索能力,，所以與FOA、GA和PSO 3種算法相比,，LFOA算法搜索精度更高,，性能更穩(wěn)定。綜合以上分析可知,，LFOA算法可較精確地搜索RVM的最優(yōu)核參數(shù),，并能達(dá)到較高的測(cè)試準(zhǔn)確率，較其他幾種算法而言,，具備一定優(yōu)勢(shì),。

4 結(jié)論

    RVM核函數(shù)參數(shù)的選取對(duì)其分類(lèi)性能有著顯著的影響。針對(duì)這一問(wèn)題,，本文采用LFOA算法對(duì)RVM核參數(shù)進(jìn)行尋優(yōu),，通過(guò)幾個(gè)典型的UCI數(shù)據(jù)集進(jìn)行測(cè)試，得出該算法可較精確地搜索到RVM的最優(yōu)核參數(shù),，具備較強(qiáng)的局部尋優(yōu)精度和全局搜索能力,，有效地提高了RVM分類(lèi)模型的性能。相比于傳統(tǒng)的果蠅算法,、遺傳算法和粒子群算法具有更高的尋優(yōu)精度和穩(wěn)定性,，為選取最優(yōu)RVM核函數(shù)參數(shù)提供了一種新方法,、新途徑。

參考文獻(xiàn)

[1] TIPPING M E.Sparse Bayesian learning and the relevance vector machine[J].Journal of Machine Learning Research,，2001,，1(3)：211-244.

[2] 范庚，馬登武,，張繼軍,，等.基于決策樹(shù)和相關(guān)向量機(jī)的智能故障診斷方法[J].計(jì)算機(jī)工程與應(yīng)用，2013,，49(14)：267-270.

[3] 張旭峰,，楊豐瑞，鄭建宏.基于RVM的可重用性SoC測(cè)試平臺(tái)設(shè)計(jì)[J].電子技術(shù)應(yīng)用,，2006,，32(5)：82-84.

[4] 陳景柱.布谷鳥(niǎo)優(yōu)化混合核相關(guān)向量機(jī)的網(wǎng)絡(luò)流量預(yù)測(cè)[J].計(jì)算機(jī)與現(xiàn)代化，2015(5)：94-97.

[5] PAN W T.A new fruit fly optimization algorithm：Taking the financial distress model as an example[J].Knowledge-Based Systems,，2012,，26(Complete)：69-74.

[6] 劉翠玲，張路路,，王進(jìn)旗,，等.基于FOA-GRNN油井計(jì)量原油含水率的預(yù)測(cè)[J].計(jì)算機(jī)仿真，2012,，29(11)：243-246.

[7] 張前圖,，房立清，趙玉龍.具有Levy飛行特征的雙子群果蠅優(yōu)化算法[J].計(jì)算機(jī)應(yīng)用,，2015,，35(5)：1348-1352.

[8] 任學(xué)平，龐震,，辛向志,，等.基于小波包最優(yōu)熵與RVM的滾動(dòng)軸承故障診斷方法[J].軸承，2014(11)：48-53.

[9] 周勇,，何創(chuàng)新.基于獨(dú)立特征選擇與相關(guān)向量機(jī)的變載荷軸承故障診斷[J].振動(dòng)與沖擊,，2012，31(3)：157-161.

[10] 姚全珠,，蔡婕.基于PSO的LS-SVM特征選擇與參數(shù)優(yōu)化算法[J].計(jì)算機(jī)工程與應(yīng)用,，2010，46(1)：134-136.

[11] 姚暢,，陳后金,，YANG Y Y，等.基于自適應(yīng)核學(xué)習(xí)相關(guān)向量機(jī)的乳腺X線(xiàn)圖像微鈣化點(diǎn)簇處理方法研究[J].物理學(xué)報(bào)，2013,，62(8)：1-11.

[12] TIPPING M E.An efficient MATLAB implementation of the sparse Bayesian modelling algorithm[CP/OL].(2009-03-12)[2016-05-10].http：//www.Relevancevector.com.

作者信息:

呂  巖,，房立清，趙玉龍,，張前圖

（軍械工程學(xué)院 火炮工程系,，河北 石家莊050003）