李吉朝1,張海英1,王惠琴2
(1.西安理工大學 復雜系統(tǒng)控制與智能信息處理重點實驗室,陜西 西安 710048;2.西安市環(huán)境監(jiān)測站,陜西 西安 710048)
摘要:BP神經(jīng)網(wǎng)絡具有較強的學習能力,但在傳統(tǒng)的研究中,隱含層節(jié)點、學習因子和動量因子往往采用試湊法得到相對較佳值,而試湊法在浪費較多時間的同時,可能得不到理想的BP神經(jīng)網(wǎng)絡輸出,這對研究造成了一定的困難。文中采用智能算法來解決BP神經(jīng)網(wǎng)絡優(yōu)化問題。遺傳算法作為一種隨機搜索算法,能夠快速尋找到全局最優(yōu)解,可以應用于本優(yōu)化問題。因此,文章采用遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡上述參數(shù),將改進后的BP神經(jīng)網(wǎng)絡運用于動力配煤非線性模型的研究。結(jié)果表明,采用遺傳算法優(yōu)化的BP神經(jīng)網(wǎng)絡具有較強的預測能力,對煤質(zhì)的發(fā)熱量預測誤差優(yōu)于線性平均模型誤差,并且仿真表明動力配煤模型為近似線性的非線性模型, BP網(wǎng)絡的輸出值誤差波動較小,結(jié)果理想。
關(guān)鍵詞:動力配煤;BP神經(jīng)網(wǎng)絡;遺傳算法;非線性
中圖分類號:TP181文獻標識碼:ADOI: 10.19358/j.issn.1674-7720.2017.09.018
引用格式:李吉朝,張海英,王惠琴.基于遺傳算法的BP神經(jīng)網(wǎng)絡優(yōu)化動力配煤模型的研究[J].微型機與應用,2017,36(9):60-63,66.
0引言
動力配煤,顧名思義是將兩種及兩種以上的單煤混合成新的煤種。動力配煤有著其必要性,首先,發(fā)電系統(tǒng)鍋爐都有其對應的設計煤種,往往由于煤種分布、資源短缺等一些客觀因素,熱電廠只能選擇綜合性價比相對較高的單煤混燒,這對鍋爐的安全穩(wěn)定運行帶來一定的影響;其次,當前環(huán)境問題愈發(fā)嚴重,我國熱力發(fā)電企業(yè)占發(fā)電行業(yè)70%左右,煤的大量使用對環(huán)境造成嚴重污染,因此,硫的排放被國家列為強制性指標。動力配煤技術(shù)可以利用某一種煤或幾種煤的長處彌補另一種或幾種煤的不足,取長補短,達到使鍋爐用煤的品質(zhì)穩(wěn)定,解決煤質(zhì)與爐型不相匹配的矛盾,使節(jié)能減排效益最大化[1]。
國內(nèi)外研究表明,動力配煤模型分為線性模型[24]與非線性模型[5],目標函數(shù)為經(jīng)濟性目標,即混煤的總金額最小,約束條件包含多種變量,包括發(fā)熱量、硫分、揮發(fā)分、灰分等。線性模型與非線性模型的判斷在于約束條件的選取,對于模型的討論,爭議不斷。近幾年,浙江大學熱工院進行過研究,得出的結(jié)論是混煤的參數(shù)模型是一個近似線性的非線性模型。但是,對于煤的一些重要參數(shù),比如發(fā)熱量,浙江大學熱工院的混煤實測值與線性加權(quán)平均值存在5%左右的誤差,這個誤差相對來說比較大,因此,動力配煤非線性模型的研究具有現(xiàn)實意義。
本研究項目來自于西安某熱電廠,電廠來煤分為高熱低硫、中熱中硫、低熱高硫三大類煤,存儲在3個煤場中,入爐煤是將這三類煤進行摻燒。

1BP神經(jīng)網(wǎng)絡的研究[6 8]
動力配煤的性能指標包括發(fā)熱量、硫分、揮發(fā)分、水份、灰分等。其中發(fā)熱量對鍋爐安全穩(wěn)定運行影響較大,硫分對環(huán)境的影響較大,本研究重點考慮這兩個性能指標,以經(jīng)濟為主要目標,鍋爐安全性以及環(huán)保性為約束條件,得到的動力配煤數(shù)學模型[9]如下:
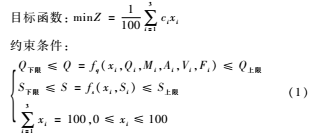
其中,目標函數(shù)中Z為混煤的平均價格,ci為單煤的單價,xi為單煤的配比,約束條件中Q為煤的發(fā)熱量,其影響因素依次為單煤的配比xi、單煤的發(fā)熱量Qi、單煤的水份Mi、單煤的灰分Ai、單煤的揮發(fā)分Vi以及單煤的固定碳Fi,約束條件中S表示煤的硫分,其影響因素依次為單煤的配比xi、單煤的硫分Si。
由動力配煤模型可知,動力配煤的約束條件為非線性,需要應用學習算法得到其模型,本研究以發(fā)熱量為例,3種煤混配輸出影響參數(shù)有18個,分別為3種單煤對應的配比、發(fā)熱量、水份、灰分、揮發(fā)分以及固定碳。因此,BP神經(jīng)網(wǎng)絡[10-13]的輸入點為18個,輸出點為1個。3層BP神經(jīng)網(wǎng)絡隱含層輸入點數(shù)的計算公式如下:
n=p+q+a(2)
其中,p為輸入層的神經(jīng)元個數(shù),q為輸出層神經(jīng)元個數(shù),a的取值范圍為0~10之間的整數(shù)。
由于BP神經(jīng)網(wǎng)絡存在兩大問題,收斂速度慢及容易陷入局部最優(yōu)。為了解決上面兩個問題,在標準BP神經(jīng)網(wǎng)絡的基礎上引進動量項,公式如下:
w(k+1)=w(k)+α[(1-η)D(k)+ηD(k-1)](3)
其中,η為學習因子,取值范圍為0.01~1;α為動量因子,取值范圍為0~1。學習因子是影響B(tài)P神經(jīng)網(wǎng)絡收斂速度的關(guān)鍵因素之一,如果學習因子太小,網(wǎng)絡的收斂速度會非常緩慢;如果學習因子太大,又會使網(wǎng)絡出現(xiàn)振蕩而無法收斂。
加入動量項的本質(zhì)是使得學習過程中的學習因子η不再是一個恒定的值,而是可以不斷變化。通常來說,動量因子不易過大,如果動量因子太大,動量項所占的比例過重,則本次誤差修正項的作用會削弱太多,以致完全不起作用,反而會延長收斂時間,甚至會引起振蕩。一般情況下,動量系數(shù)的最大值在0.9左右。
在以往的BP學習過程中,往往通過經(jīng)驗來選取隱含層節(jié)點數(shù)、學習因子以及動量因子,使得BP神經(jīng)網(wǎng)絡達不到最佳性能,因此,本研究運用遺傳算法[1418]對上述3個參數(shù)進行優(yōu)化,目標函數(shù)為BP神經(jīng)網(wǎng)絡的輸出誤差。圖1為遺傳算法優(yōu)化BP神經(jīng)網(wǎng)網(wǎng)絡流程圖。
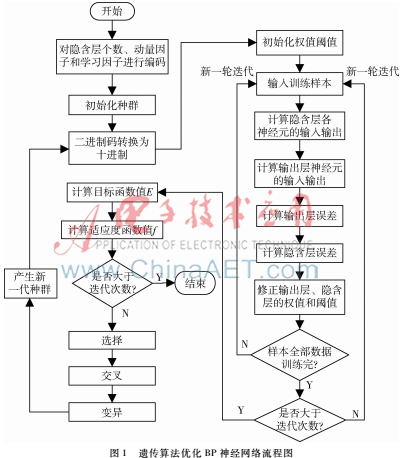
2種群的編碼
本研究種群編碼采用二進制編碼,將隱含層節(jié)點、學習因子以及動量因子串成一個字符串,其中隱含層節(jié)點范圍為0~14,學習因子以及動量因子的范圍均為0~100,初始種群數(shù)目為20個。隱含層節(jié)點為4位二進制數(shù),學習因子為7位二進制數(shù),動量因子為7位二進制數(shù),因此二進制編碼為18位。如果參數(shù)a的變化范圍為[amin,amax],用m位二進制數(shù)b來表示,則二者之間滿足:
a=amin+b2m-1(amax-amin)(4)
由于隱含層節(jié)點必須為大于0的整數(shù),因此這里需要對其向上取整。
3目標函數(shù)值計算
將BP神經(jīng)網(wǎng)絡改寫成function函數(shù),形式如下:
E=mubiao(a,b,c)(5)
其中a為隱含層節(jié)點數(shù),b為學習因子,c為動量因子,E為網(wǎng)絡輸出的總誤差,即為遺傳算法的目標函數(shù),這里的E越小,網(wǎng)絡越好。
4適應度函數(shù)的選擇
目標函數(shù)是極小值,那么對于適應度的函數(shù)有下面兩種表示方法:

第一種方法由于E數(shù)值過小,得到的差值f1基本相同,所以不適用,因此選擇第二種適應度計算公式,不過進行了改進,由于E的數(shù)值為10-3級,先對目標函數(shù)值歸一化處理,處理公式如下:

經(jīng)過歸一化處理的目標函數(shù)分布在0~1范圍內(nèi),接下來對歸一化后的目標函數(shù)放大到0~100范圍內(nèi),放大函數(shù)為:

所求得f即為適應度值。選擇輪盤賭法,適應值越大,被選擇的概率越高。選擇概率計算公式為:
pi=fi∑ni=1fi(9)
5仿真結(jié)果
實驗研究發(fā)現(xiàn),網(wǎng)絡輸出的值均勻分布在實測值的兩端,并且具有較好的預測能力。遺傳算法尋優(yōu)得到的隱含層節(jié)點為6個,學習因子為0.3,動量因子為0.1。
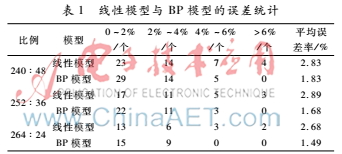
本文中所采用數(shù)據(jù)來自于參考文獻[9],每3種煤按特定比例摻配,總共有48個樣本,網(wǎng)絡輸入層為18個節(jié)點,輸出層為1個節(jié)點,將3種煤的順序調(diào)換可以擴展為288個樣本,由于學習樣本數(shù)量有限,并且BP神經(jīng)網(wǎng)絡學習預測能力的強弱取決于學習樣本的數(shù)量,因此本文將288個樣本絕大多數(shù)作為學習樣本,少量作為預測樣本,并且學習樣本做到包含全部配比信息。分別按照學習樣本與預測樣本之比為240∶48、252∶36、264∶24做了3次仿真,其統(tǒng)計結(jié)果如表1所示。
仿真圖選取的配比為262∶24,仿真結(jié)果如圖2~圖6所示。
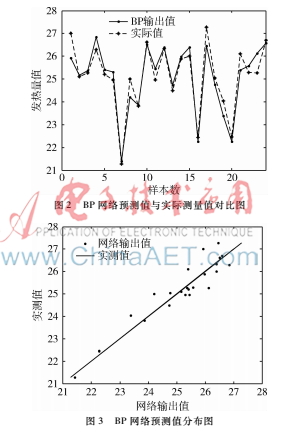


圖2中,經(jīng)過遺傳算法優(yōu)化參數(shù)之后的BP神經(jīng)網(wǎng)絡具有較強的預測能力,BP網(wǎng)絡輸出值能夠較好地跟隨實測值上下波動,因此為單煤摻配后熱值具有非線性提供了較好的依據(jù)。
圖3中,可以看出網(wǎng)絡輸出值分布在實測值附近,偏離較小,網(wǎng)絡預測能力較強。
圖4中,線性平均值也能夠較好地逼近實測值,但是存在少量誤差較大的點,其逼近效果較網(wǎng)絡預測差。
圖5中,線性平均值散落在實測值附近,可以明顯看出線性平均值比網(wǎng)絡預測值差。
從圖6中可以看出,線性平均值與實測值誤差率較大,并且存在較大的波動,BP輸出值與實測值誤差率相對較小,并且比較平穩(wěn)。
6結(jié)束語
首先,遺傳算法具有較強的尋優(yōu)能力,但是對于目標函數(shù)的值較大,并且作為適應度時,對于遺傳算法的收斂存在較大的影響,作為輪盤賭法,比如兩個適應度值49 000與50 000,尋優(yōu)過程中可能會錯誤地認為50 000為最小值,因為兩者概率都比較接近50%,但是實驗者可以判斷出49 000為最小值。因此,在此基礎上本文創(chuàng)新性地提出適應度歸一化,放大兩個相接近的較大適應度值之間的差距,提高淘汰率,并且加快收斂速度。
其次,依靠試湊法得到BP神經(jīng)網(wǎng)絡往往浪費時間,而且得不到理想模型。本文創(chuàng)新性地通過遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡的隱含層節(jié)點、學習因子和動量因子,使BP神經(jīng)網(wǎng)絡的預測能力達到相對最佳,減少依靠試湊法帶來的隨機性。實驗表明,該方法得到的BP神經(jīng)網(wǎng)絡預測能力較強;動力配煤非線性模型與線性模型接近,但是,非線性模型的輸出值與實測值的誤差小于線性模型的輸出與實測值的誤差,并且誤差更加平穩(wěn)。因此,本文認為動力配煤模型為近似線性模型的非線性模型。
參考文獻
[1] 屈國強.動力配煤優(yōu)化研究現(xiàn)狀及展望[J].潔凈煤技術(shù),2015,21(6):6-10,14.
[2] 谷麗景,李永華,李路.電站鍋爐燃燒優(yōu)化混合模型預測[J].中國電機工程學報,2015,35(9):2231-2237.
[3] 李彬,尉守科,于俊清,等.火電企業(yè)配煤模型與優(yōu)化算法[J].計算機工程與設計,2015,36(9):2388-2394.
[4] 夏季,張成,袁向宇,等.基于物理規(guī)劃的混煤摻燒方案優(yōu)化模型[J].煤炭學報,2015,40(11):2654-2660.
[5] 陸潘. 煙煤摻燒印尼煤的動力配煤模型研究[D].武漢:華中科技大學,2011.
[6] 劉春艷,凌建春,寇林元,等.GABP神經(jīng)網(wǎng)絡與BP神經(jīng)網(wǎng)絡性能比較[J].中國衛(wèi)生統(tǒng)計,2013,30(2):173-176,181.
[7] 黃忠棋.基于BP神經(jīng)網(wǎng)絡的墻地磚缺陷檢測技術(shù)研究[J].微型機與應用,2014,33(23):81-83.
[8] 劉天舒.BP神經(jīng)網(wǎng)絡的改進研究及應用[D].哈爾濱:東北農(nóng)業(yè)大學,2011.
[9] 李穎.基于非線性理論的動力配煤模型的研究[D].杭州:浙江大學,2002.
[10] Liao Yanfen, Wu Changhong, Ma Xiaoqian.New hybrid optimization model for power coal blending[C].International Conference on Machine Learning and Cybernetics. IEEE, Guangzhou, China, 2005(7):4023-4027.
[11] DESHPANDE P, WARKE N, KHANDARE P,et al.Thermal power plant analysis using artificial neural network[C].Nirma University International Conference on Engineering,2012:16.
[12] 李松,劉力軍,解永樂.遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡的短時交通流混沌預測[J].控制與決策,2011,26(10):1581-1585.
[13] Cheng Jun, Wang Xin, Si Tingting, et al.Ignition temperature and activation energy of power coal blends predicted with backpropagation neural network models[J]. Fuel,2016,173(1):230-238.
[14] Hao Zhou, Qian Xinping, Cen Kefa, et al.Optimizing pulverized coal combustion performance based on ANN and GA[J]. Fuel Processing Technology, 2004, 85(23):113-124.
[15] 夏季,華志剛,彭鵬,等.基于非支配排序遺傳算法的無約束多目標優(yōu)化配煤模型[J].中國電機工程學報,2011,31(2):8590.
[16] 劉玉嬌,張海英,關(guān)海盈.基于多種算法的多目標配煤優(yōu)化方法[J].熱力發(fā)電,2014,43(9):108-112.
[17] 燕禮富,鄧全亮,范懌濤.基于預測模型和遺傳算法的配煤優(yōu)化研究[J].計算技術(shù)與自動化,2010,29(3):31-34.
[18] Guo Xijin, Chen Ming, Wu Jiawei.Coal blending optimization of coal preparation production process based on improved GA[J]. Procedia Earth and Planetary Science, 2009, 1(1):654-660.

