0 引言

    四旋翼飛行器是多旋翼飛行器中的一種。它有4個(gè)轉(zhuǎn)子,，被放置在距離飛行器質(zhì)量中心等距的方形結(jié)構(gòu)中,。飛行器通過調(diào)整電機(jī)轉(zhuǎn)子轉(zhuǎn)速來(lái)進(jìn)行姿態(tài)位置控制，正是由于這種簡(jiǎn)單的結(jié)構(gòu)設(shè)計(jì),，使其能夠垂直升降,、懸停及其靈活的機(jī)動(dòng)性，被廣泛用于城市交通監(jiān)控,、測(cè)繪,、搜尋、救援和施工檢查等應(yīng)用中,。

    四旋翼飛行器由于在飛行過程中有許多不確定因素,，具有復(fù)雜的空氣動(dòng)力學(xué)特性^[1-3],，使學(xué)者們?cè)谒男盹w行器控制方法和控制器的設(shè)計(jì)等方面做了許多的研究。其中包括反步控制,、非線性H_∞控制,、LQR控制器等。實(shí)驗(yàn)結(jié)果表明在大角度時(shí),，采用非線性控制方法能夠取得良好的控制效果^[4],，反步法設(shè)計(jì)的控制器在相對(duì)高擾動(dòng)下取得了很好的姿態(tài)角控制效果^[5]。

    這些控制器在姿態(tài)控制等方面雖然有比較好的效果,，但由于其控制算法需要建立準(zhǔn)確的數(shù)學(xué)模型,，計(jì)算量大，數(shù)據(jù)的實(shí)時(shí)處理對(duì)處理器性能要求特別高,，實(shí)現(xiàn)起來(lái)有一定的困難,。為此本文設(shè)計(jì)了一種易于實(shí)現(xiàn)的、能夠快速穩(wěn)定的對(duì)四旋翼飛行器實(shí)現(xiàn)姿態(tài)控制的串級(jí)PID控制器,。

1 四旋翼飛行器的基本工作原理

    四旋翼飛行器是通過改變兩對(duì)正反螺旋槳的轉(zhuǎn)速來(lái)實(shí)現(xiàn)對(duì)機(jī)體的運(yùn)動(dòng)控制,。如圖1所示，在平衡狀態(tài)下,，電機(jī)1和3的螺旋槳逆時(shí)針旋轉(zhuǎn),，而電機(jī)2和4的螺旋槳順時(shí)針旋轉(zhuǎn)，但產(chǎn)生正方向上的升力,，這樣當(dāng)飛行器4個(gè)螺旋槳有相同的轉(zhuǎn)速時(shí),，所產(chǎn)生的反旋轉(zhuǎn)力矩正好可以互相抵消。

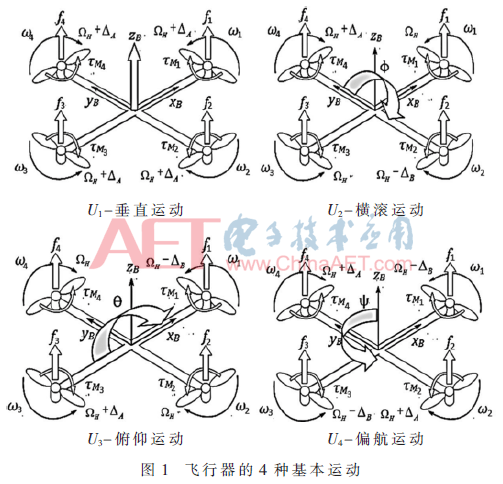
    四旋翼飛行器是一個(gè)四輸入,、六輸出的欠輸入控制系統(tǒng),，需要選擇4個(gè)合適的控制變量：垂直運(yùn)動(dòng)推力U₁、橫滾(Roll)運(yùn)動(dòng)U₂,、俯仰(Pitch)運(yùn)動(dòng)U₃和偏航(Yaw)運(yùn)動(dòng)U₄,，對(duì)系統(tǒng)進(jìn)行解耦，從而使飛行器更加容易控制,。假設(shè)飛行器懸停時(shí)4個(gè)螺旋槳轉(zhuǎn)速為Ω_H,，改變螺旋槳轉(zhuǎn)速變化量Δ_A和Δ_B值相等、符號(hào)相反,，以至于推力U1不發(fā)生變化,，從而使飛行器不會(huì)爬升或下降，來(lái)產(chǎn)生俯仰,、橫滾和偏航運(yùn)動(dòng),。

2 四旋翼飛行器的數(shù)學(xué)模型

    為方便飛行器的建模,，定義兩個(gè)坐標(biāo)系：慣性坐標(biāo)系（北東天坐標(biāo)系）,、機(jī)體坐標(biāo)系,。其中慣性坐標(biāo)系在地面，機(jī)體坐標(biāo)系與飛行器固聯(lián),，如圖2所示,。

    為方便分析建模作兩點(diǎn)假設(shè)：(1)四旋翼飛行器是剛體，質(zhì)心和機(jī)體坐標(biāo)系原點(diǎn)重合,；(2)機(jī)體坐標(biāo)系的主軸和機(jī)體的慣性主軸相重合,。

2.1 運(yùn)動(dòng)學(xué)方程建立

2.2 牛頓歐拉方程建立

    由假設(shè)(1)，根據(jù)牛頓歐拉方程,，飛行器動(dòng)力學(xué)方程為：

    使用葉素動(dòng)量理論可以推導(dǎo)出螺旋槳所產(chǎn)生的力和旋轉(zhuǎn)力矩與它的轉(zhuǎn)速平方成正比^[3,，6]。

    推力和旋轉(zhuǎn)力矩之間的關(guān)系由下式描述：

式中,，l為電機(jī)到飛行器中心距離,，k_F為推力系數(shù)，k_M為旋轉(zhuǎn)力矩系數(shù),。

    飛行器位置控制相對(duì)于慣性坐標(biāo)系,，姿態(tài)控制相對(duì)于機(jī)體坐標(biāo)系，定義混合坐標(biāo)系,，包含相對(duì)于慣性坐標(biāo)系的位置信息和相對(duì)于機(jī)體坐標(biāo)系的姿態(tài)信息[6],，速度角速度矢量如下：

    由式(9)知，以U₁,、U₂,、U₃、U₄為系統(tǒng)輸入可以控制機(jī)體的位置和姿態(tài)6個(gè)自由度的運(yùn)動(dòng),，從而對(duì)系統(tǒng)進(jìn)行解耦,，解決了飛行器欠驅(qū)動(dòng)控制問題。

3 四旋翼飛行器的控制系統(tǒng)構(gòu)建

    由式(3)和式(9)可知,，歐拉角及其對(duì)時(shí)間的微分不依賴位置運(yùn)動(dòng),，而位置運(yùn)動(dòng)依賴于歐拉角。將系統(tǒng)的運(yùn)動(dòng)分為兩個(gè)子系統(tǒng)：姿態(tài)運(yùn)動(dòng)M₁(在機(jī)體坐標(biāo)系中)和位置運(yùn)動(dòng)M₂(在慣性坐標(biāo)系),。飛行器內(nèi)部控制結(jié)構(gòu)如圖3所示,。

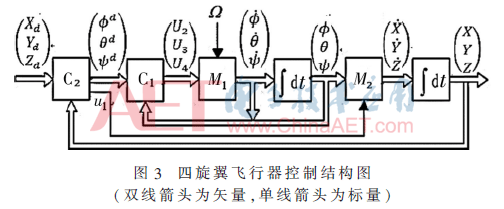
    C₁為內(nèi)回路控制器，C₂為外回路控制器,。由圖4可知,，四旋翼飛行器的控制系統(tǒng)分為內(nèi)回路和外回路，內(nèi)回路為姿態(tài)控制是外回路位置控制的基礎(chǔ),，通過控制飛行器的3個(gè)歐拉角,，實(shí)現(xiàn)對(duì)飛行器的姿態(tài)控制，進(jìn)而實(shí)現(xiàn)對(duì)飛行器位置控制。

4 控制器設(shè)計(jì)及系統(tǒng)仿真

    根據(jù)以上分析對(duì)系統(tǒng)設(shè)計(jì)串級(jí)PID控制器,，內(nèi)回路為姿態(tài)控制,，外回路為位置控制。

4.1 線性化數(shù)學(xué)模型

    在實(shí)際飛行中俯仰角θ,、滾轉(zhuǎn)角φ,，角速度矢量ω^B比較小。假設(shè)在飛行中偏航角ψ=ψ₀保持不變,，其中ψ₀為初始偏航角,。在定高或懸停的穩(wěn)態(tài)附近，有：

4.2 內(nèi)回路：姿態(tài)控制回路

    在PID控制器中,，比例（p）和積分（I）能夠提高穩(wěn)態(tài)精度,，但積分環(huán)節(jié)的加入降低了系統(tǒng)穩(wěn)定性和響應(yīng)速度，系統(tǒng)很容易發(fā)散,。微分（D）不但能夠提高系統(tǒng)穩(wěn)定性,，而且能夠提高系統(tǒng)響應(yīng)速度。因此,，內(nèi)回路設(shè)計(jì)PD控制器對(duì)飛行器進(jìn)行姿態(tài)控制,。

    由式(10)設(shè)計(jì)PD控制器，可得：

    結(jié)合式(7),、式(11)可得到期望姿態(tài)角與期望轉(zhuǎn)速之間的關(guān)系,。

4.3 外回路：位置控制回路

    由圖3可知，系統(tǒng)輸入為期望位置量,，經(jīng)過外環(huán)控制器轉(zhuǎn)換為期望的姿態(tài)角,，作為內(nèi)環(huán)的輸入。

4.4 搭建系統(tǒng)仿真控制回路

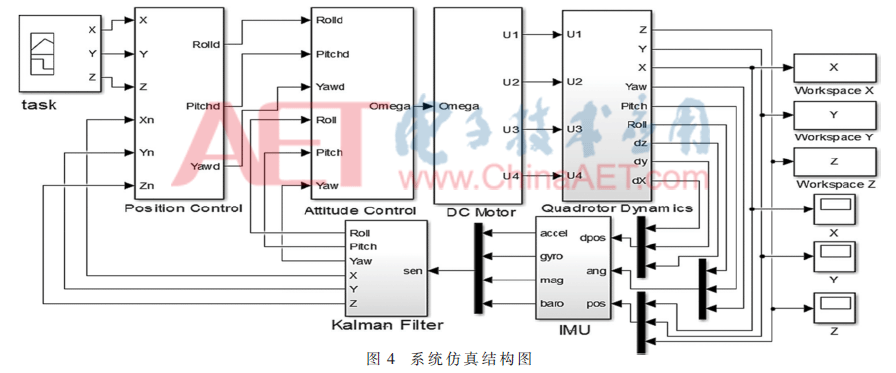
    如圖4所示,，系統(tǒng)仿真結(jié)構(gòu)包括：位置控制,、姿態(tài)控制、電機(jī)動(dòng)力學(xué)模型,、飛行器動(dòng)力學(xué)模型,、IMU和Kalman(傳感器建模與濾波器設(shè)計(jì)，包括陀螺儀,、加速度計(jì),、磁羅盤、氣壓計(jì),，考慮傳感器在測(cè)量過程中的噪聲與漂移,，設(shè)計(jì)卡爾曼濾波器，輸出準(zhǔn)確的位置和姿態(tài)信息,，使仿真更加真實(shí)可靠),。仿真參數(shù)如表1所示。

4.5 仿真結(jié)果

    (1)定點(diǎn)懸停

    在零初始條件下，輸入r^d=(X^d,，Y^d,，Z^d)=(5，10,，15)時(shí)，系統(tǒng)位置輸出如圖5所示,。

    飛行器在運(yùn)動(dòng)中無(wú)超調(diào),，運(yùn)行平穩(wěn)，在8 s左右到達(dá)目標(biāo)位置,，最終穩(wěn)定在X,、Y、Z軸位置分別為5.001 5,、10.013 6,、15.008 6，誤差非常小,，滿足控制要求,。

    (2)位置跟蹤

    在零初始條件下，X軸輸入為斜坡信號(hào)r^d=(X^d,，Y^d,，Z^d)=(t，10,，20),，0≤t≤20 s，系統(tǒng)位置輸出如圖6所示,。

    當(dāng)X軸輸入為斜坡信號(hào)時(shí),，在3 s左右，追蹤到了斜坡信號(hào),，3 s之后追蹤誤差非常小,，Y軸和Z軸在8 s左右進(jìn)入穩(wěn)定狀態(tài)，飛行器在整個(gè)運(yùn)動(dòng)中無(wú)超調(diào),，運(yùn)行平穩(wěn),，最終穩(wěn)定在X、Y,、Z軸位置分別為20.001 5,、10.020 3、15.006 5,，誤差非常小,，滿足控制要求。

5 總結(jié)

    本文主要研究了基于四軸飛行器的串級(jí)PID控制算法。在內(nèi)回路姿態(tài)控制設(shè)計(jì)PD控制器,，外回路位置控制設(shè)計(jì)PID控制器,，仿真結(jié)果表明：(1)所設(shè)計(jì)控制算法能夠快速、穩(wěn)定地對(duì)四旋翼飛行器實(shí)現(xiàn)姿態(tài)位置控制,；(2)所設(shè)計(jì)的控制算法有比較好的軌跡追蹤能力,；(3)對(duì)外界干擾具有比較好的魯棒性；(4)該控制器易于移植到實(shí)驗(yàn)平臺(tái)上,，進(jìn)一步驗(yàn)證控制算法的正確性,。

參考文獻(xiàn)

[1] HOFFMANN G M，HUANG H,，WASLANDER S L,，et al.Quadrotor helicopter flight dynamics and control：Theory and experiment[C].Proceedings of the AIAA Guidance，Navigation and Control Conference and Exhibit,，2007.

[2] HUANG H,，HOFFMANN G M，WASLANDER S L,，et al.Aerodynamicsand control of autonomous quadrotor helicopters in aggressive maneuvering[C].IEEE International Conference on Robotics and Automation,，2009：3277-3282.

[3] MAHONY R，KUMAR V,，CORKE P.Multirotor arial vehicles,，modeling estimation and control of quadrotors[J].IEEE Robot & Automat.Magazine，2012,，19(3)：20-32.

[4] CASTILLO P,，DZUL A，LOZANO R.Real-time stabilization and tracking of a four-rotor mini rotorcraft[J].Transactions on Control Systems Technology,，2004,，12(4)：510-5l6.

[5] BOUABDALLAH S，SIEGWART R．Backstepping and sliding-mode techniques applied to an indoor micro quadrotor[C].In Proceedings of the International Conference on Robotics and Automation．Barcelona：IEEE,，2005：2247-2252.

[6] BRESCIANI T.Modelling,，identification and control of a quadrotor helicopter[D].M.S.thesis，Dept.of Automatic Control,，Lund Univ.,，Lund，Sweden.2008.

[7] 何勇靈,，陳彥民,，周岷峰.四旋翼飛行器在風(fēng)場(chǎng)擾動(dòng)下的建模與控制[J].中國(guó)慣性技術(shù)學(xué)報(bào)，2013,，2(5)：624-630．

作者信息:

薛佳樂,，程  珩

（太原理工大學(xué) 機(jī)械工程學(xué)院,，山西 太原030024）