宋洪宇,史小宏

　　(上海海事大學 信息工程學院,，上海 201306)

　　摘要：為了解決復雜系統(tǒng)的可靠性和任務(wù)成本評估問題,，提出混合冗余備用系統(tǒng)設(shè)計模式。通過概率統(tǒng)計分布方法來計算復雜系統(tǒng)元件的可靠性和任務(wù)成本,，利用蟻群和遺傳相結(jié)合的混合算法來解決備用元件的最優(yōu)分布問題,。最后通過仿真實驗計算出系統(tǒng)的可靠性和任務(wù)成本，以及備用元件的優(yōu)化分布序列,，在滿足一定的系統(tǒng)可靠性的基礎(chǔ)上使得備用元件的操作成本最小化,。

　　關(guān)鍵詞：冗余備用,；可靠性；任務(wù)成本,；蟻群遺傳算法,；最優(yōu)分布

　　中圖分類號：TP302.8文獻標識碼：ADOI： 10.19358/j.issn.1674-7720.2017.10.012

　　引用格式：宋洪宇,史小宏.基于蟻群遺傳算法的冗余備用元件優(yōu)化研究［J］.微型機與應(yīng)用，2017,36（10）：40-43,，47.

0引言

　　復雜系統(tǒng)在工作中時常會出現(xiàn)故障,，為了保障其可靠性，其中一個廣泛使用的技術(shù)就是冗余備用［1］：一個或多個元件處于工作狀態(tài)下,，當有一個正在工作的元件出現(xiàn)故障的時候,，就會有一個備用元件被激活來替換這個出現(xiàn)故障的元件，保證系統(tǒng)能夠繼續(xù)運行下去,。常用的冗余類型有熱備份和冷備份［2］,，當元件處于熱備用模式下的時候，一旦工作中的元件出現(xiàn)故障,，熱備用元件可以提供快速恢復,。為了確保系統(tǒng)能夠隨時替換出現(xiàn)故障的工作元件,，就需要時刻補充熱備用模式下的元件,。由于熱備用中的元件一直處于工作中，這就增加了系統(tǒng)的成本開銷和能源消耗,，與此相比,，處于冷備用模式下的元件是低成本的，但是當它去替換工作中失效的元件時,，需要長時間的恢復延遲,。

　　考慮到冷熱備用各自的優(yōu)缺點，提出混合冗余備用系統(tǒng)模式,，即讓較少的元件處于熱備用模式下,，可以隨時快速地替換出現(xiàn)故障的工作元件，讓大部分元件處于冷備用模式下,，當熱備用模式下的元件用完后,，處于冷備用模式下的元件會轉(zhuǎn)移到熱備用模式下［3］。這種冗余備用模式不僅保留了熱備用模式快速替換的特點,，還大大提高了系統(tǒng)的可靠性,，與此同時，處于冷備用模式下的元件運行成本低,，又大大降低了系統(tǒng)的成本開銷,。

　　最后，當冗余元件滿足系統(tǒng)可靠性時,，使用離散數(shù)學的概率分布方法來計算系統(tǒng)可靠性和預期任務(wù)成本,。冗余備用模式下的元件分布和啟動順序?qū)ο到y(tǒng)的可靠性和成本會產(chǎn)生嚴重的影響［4］，利用蟻群遺傳混合算法來優(yōu)化冗余備用模式下的元件，分析備用元件在冗余模型中的不同分配對系統(tǒng)可靠性和預期任務(wù)成本的影響,，并找出最優(yōu)元件分布和初始化順序［5］,。

1元件的混合冗余備用模型

　　假設(shè)系統(tǒng)中有N個獨立的備用元件s(1),s(2),…，s(N),，讓H個備用元件處于熱備用模式下,，當系統(tǒng)開始運行的時候，對s(1),s(2),…,，s(H)進行了初始化,，剩下的N－H個備用元件s(H+1),…,s(N)處于冷備用模式下。

　　當系統(tǒng)中運行的工作元件失效時,，處于熱備用模式下的元件會立刻替換失效元件,；當熱備用模式下的元件用完后，處于冷備用模式下的元件進行初始化,。

　　為了方便求得系統(tǒng)可靠性,，提出一些附加假設(shè)：

　　（1）系統(tǒng)中的元件數(shù)量和類型是固定的,；

　?。?）元件之間相互獨立；

　?。?）和任務(wù)時間相比,，替換失效元件的時間可以忽略不計；

　?。?）工作中的元件和備用元件的失效是不可修復的,。

　　1.1故障元件概率計算

　　將整個運行時間t分成m個相同的時間單元，即Δ=t/m,，備用元件k在第i個時間單元失效的概率為pk(i),，每個備用元件有相同的累計失效分布函數(shù)Fk(t)。假設(shè)指數(shù)分布的時間失效率為λk,，那么

　　Fk(t)=1－exp(－λkt)（1）

　　pk(i)=［1－exp(－λkΔ)］exp(－λkΔi)（2）

　　根據(jù)韋伯分布提供的規(guī)模參數(shù)ηk以及狀態(tài)參數(shù)βk,，得到的分布函數(shù)和概率密度函數(shù)公式如下：

　　Fk(t)=1－exp(－(t/ηk)βk)（3）

　　pk(i)=exp{－［Δi/ηk］βk}－exp{－［Δ(i+1)/ηk］βk}（4）

　　考慮到備用元件的失效分布時間Tk是離散的而不是連續(xù)的，假設(shè)Tk的概率質(zhì)量函數(shù)用向量表示為pk={pk(0),…,pk(m)},，pk(i)=Pr{Δi≤Tk<Δ(i+1)}(0≤i<m）,，pk(i)表示備用元件k在第i個時間間隔失效的概率。

　　由于系統(tǒng)元件的運行時間不會超過任務(wù)時間t,，在整個任務(wù)結(jié)束之前元件k不會失效的概率為：pk(m)=Pr{Tk≥t=Δm}就可以表示為：

　　1.2系統(tǒng)元件的失效時間分布

　　根據(jù)前面給出模型的描述可知,，當k=H+1時，說明熱備用模式下的元件已經(jīng)用完,，系統(tǒng)中冷備用模式下的元件在第k－1個元件出現(xiàn)失效時便進行初始化,。當系統(tǒng)中第k個備用元件從運行時間開始到間隔Xk發(fā)生失效時,，向量為Qk=(Qk(0),…,Qk(m))，可知,，Qk(i)=Pr{Xk=Δi},。若備用元件s(1)在運行時間開始時進行初始化，便有X1=Ts(1)和Q1(i)=ps(1)(0≤i≤m),。熱備用模式下的冗余元件在運行時間開始時便進行初始化,，可知Xk=max(Xk－1,Th(k))，那么熱備用模式下的冗余元件可靠性公式為：

　　當熱備用模式下的元件全部使用完或發(fā)生失效時,，處于冷備用模式下的元件便會進行初始化,，可知Xk=Xk－1+Th(1)，冷備用模式下的元件可靠性公式有：

　　Qk(i)=∑ij=0Pr{Xk－1=Δj}Pr{Th(k)=Δ(i－j)}

　　=∑ij=0Qk－1(z)ph(k)(i－j)（7）

　　Qk(m)=∑m－1j=0Pr{Xk－1=Δj}∑mn=m－jPr{Th(k)=Δn}

　　=∑m－1j=0Qk－1(j)∑mn=m－jph(k)(n)（8）

　　1.3系統(tǒng)可靠性和預期成本計算

　　根據(jù)上面的研究工作,，備用元件的系統(tǒng)可靠性和預期成本評估算法如下：

　　C=R=0,Q0(1)=1,Q0(i)=0(2<=i<=m)

　　for k=1,…,H

　　set Qk(j)=0(1<=j<=m)

　　C=C+Vh(k)

　　for i=0,…,m;C=C+△*i*w h(k)*p h(k)(i)

　　for z=0,…,m-1

　　for i=0,…,m

　　j = max(z,i)

　　Qk(j)=Qk(j)+Q k-1(z)*p h(k)(i)

　　R=R+Qk(m)

　　for k=H+1,…,N

　　set Qk(j)=0(0<=j<=m)

　　C = C+V h(k)(1-Q k-1(m))+△*m*

　　W h(k)*Q k-1(m)

　　for i 0=0,…,m-1

　　C = C+△*i0*W h(k)*Q k-1(i0)

　　fori=0,…,m

　　j =i +i0

　　if (j>m) j=m

　　C=C+△*(j-i0)*w h(k)*Q k-1(i0)*

　　p h(k)(i)

　　Q k(j)=Q k(j)+Q k-1(i0)*p h(k)(i)

　　R = R + Q k(m)

2蟻群遺傳算法元件優(yōu)化

　　2.1蟻群遺傳算法的思想

　　遺傳算法［6］具備全局搜索能力,，能夠迅速地搜索出解空間中的全部解，通過其內(nèi)在并行性進行分布式計算,，求解速度明顯加快,。缺點是沒有很好地使用系統(tǒng)反饋回來的信息，使搜索產(chǎn)生盲目性,，降低了最優(yōu)解的收斂速度,，致使計算最優(yōu)解效率較低。蟻群算法［7］是一種基于種群的優(yōu)化算法,，它由多只螞蟻共同構(gòu)建解路徑,，該算法根據(jù)在解路徑上遺留且互換信息素來實現(xiàn)優(yōu)化過程,，提高了解路徑的效率,。擁有正反饋機制，利用信息素的持續(xù)變化以及收斂得到優(yōu)化解,。然而,，由于缺少初始信息素，因此信息的積累過程比較耗時,。

　　蟻群遺傳算法［89］就是把蟻群算法和遺傳算法組合起來,，把遺傳算法引入到蟻群算法迭代中，把遺傳算法每一次父類計算生成的解當成蟻群算法的初始群體,，根據(jù)蟻群算法的多次循環(huán),，加快收斂速度，提高求解效率并找到最優(yōu)解［10］,。本文采用遺傳算法進行遺傳算子操作,，生成合適的解作為蟻群算法的初始信息素，利用蟻群算法進行螞蟻路徑轉(zhuǎn)移和信息素的更新［11］,，獲得最優(yōu)解,。

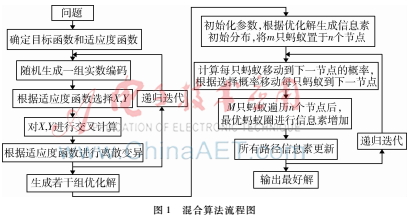
　　2.2蟻群遺傳算法的優(yōu)化過程

　?。?）定義目標函數(shù)和適應(yīng)度函數(shù)，計算每個個體的適應(yīng)度fi,，對種群規(guī)模中的個體進行如下遺傳操作,，從而產(chǎn)生下一代個體。

　?、龠x擇算子,，使用遺傳算法中的輪盤賭方法，種群中個體適應(yīng)度函數(shù)值越大,，被選擇的機率就越高,。

　　②交叉算子,，利用實數(shù)編碼,，交叉操作使用算術(shù)交叉算子，首先隨機確定參與交叉的父代,，接著進行兩兩配對,，父代中的個體X和Y按照式(9)產(chǎn)生兩個新的個體:

　　X′=eX+(1－e)Y

　　Y′=(1－e)X+eY′（9）

　　其中e∈(0,1)

　　③變異算子,，采用離散突變算子［12］,，用特定概率對父代中每個個體進行變異，返回突變后的個體并放入新種群中,。

　　(2)反復執(zhí)行選擇,、交叉、變異操作,，直至達到遺傳算法結(jié)束前提,。假定最少循環(huán)次數(shù)為Nmin，最多循環(huán)次數(shù)為Nmax,，在遺傳算法的迭代過程中計算進化率,，公式如下:

　　f-=(fn－fn－1)/∑ni=1fi（10）

　　如果持續(xù)三次進化速率不大于最小進化速率，則結(jié)束遺傳算法的循環(huán),，開始執(zhí)行蟻群算法,。

　　（3）當遺傳算法運行完畢后,，將產(chǎn)生的適應(yīng)度強的后代加入到新組合中,。

　　（4）依據(jù)優(yōu)化解得出吸引強度初始分布,，使用蟻群算法信息素的初始值設(shè)定方法,，求出其信息素初始值τ，有τ=τc+τg,，其中τc表示給出的信息素常量,，τg表示遺傳算法求得結(jié)果轉(zhuǎn)換的信息素值,。

　　（5）m只螞蟻被放置在它們各自的初始節(jié)點上,，計算每只螞蟻從i節(jié)點移動到j(luò)節(jié)點的移動概率pm(i,j）,，依據(jù)移動概率轉(zhuǎn)移每只螞蟻到下一節(jié)點，并且執(zhí)行信息素局部更新,。

　?。?）判斷所有螞蟻是否已生成整個路徑［13］，若還沒有生成整體路徑則執(zhí)行步驟（5）,，否則,，執(zhí)行步驟（7）。

　?。?）比較所有的可行解, 輸出最優(yōu)解,。

　　整個過程的流程圖如圖1所示。

　　由于備用元件的初始化順序強烈地影響著系統(tǒng)的可靠性和預期任務(wù)成本,，接下來要解決的問題就是找出混合冗余備用元件的最優(yōu)分布序列,，當達到相應(yīng)可靠性級別R*時，使得系統(tǒng)的花銷最小化,。

　　min C s.t R≥R*(11)

　　將備用元件的初始化序列用染色體來表示,，尋找存在于熱備用模式和冷備用模式下的冗余元件，根據(jù)前面求可靠性和任務(wù)成本的計算方法,，能夠得出系統(tǒng)中備用元件按照相應(yīng)順序時的可靠性R和預期任務(wù)成本C,，接下來再根據(jù)公式(11),先設(shè)定Ω=M-C-σmin{0,R*－R}，其中M是一個非常大的整數(shù),，通過此式來解決系統(tǒng)冗余元件的優(yōu)化分布問題,當σ=0時,，能夠計算出系統(tǒng)最小任務(wù)成本開銷，當σ變大且R*=1時,，就變成了計算系統(tǒng)元件的最大可靠性問題,。

　　當蟻群遺傳算法進行時，從0~N的隨機數(shù)字中選擇一組數(shù)據(jù)組合作為解決方案,，任意生成的集合表示系統(tǒng)中冗余備用元件的初始化序列，例如{3,1,4,6,2,5}這組數(shù)字組合,，3,1,4表示熱備用冗余元件的初始化序列,，利用遺傳算法交叉和變異的手段得到新的解決方案，進而求出適應(yīng)度函數(shù)值,，接著把求得的初始化序列放入到上一節(jié)的可靠性和任務(wù)成本計算方法里,，得出這種狀況下的可靠性和預期任務(wù)成本，并帶入公式(11)中去判斷得出的適應(yīng)度函數(shù)值是否滿足需求,，然后根據(jù)蟻群算法信息素的初始值設(shè)定方法,，求出其信息素初始值并進行信息素局部更新,，獲得新的個體保留最優(yōu)解，直到蟻群遺傳算法計算出一組元件初始化列表,，當求出的系統(tǒng)可靠性滿足公式(11)時,，蟻群遺傳算法終止，保留最優(yōu)解情形下的備用元件的初始化列表,。

3仿真結(jié)果與分析

　　3.1模擬計算結(jié)果與分析

　　本節(jié)通過仿真實驗來實現(xiàn)模型,，假定一個復雜多態(tài)系統(tǒng)中含有6個備用冗余元件，系統(tǒng)中元件的失效狀態(tài)能夠使用韋伯失效分布模型來表述,，表1提供了韋伯規(guī)模參數(shù)ηk和狀態(tài)參數(shù)βk,。此外，表1還提供了冷備用和熱備用模式下的冗余元件的啟動開銷,，設(shè)定系統(tǒng)的總運行時間t=300,，當m=500時，前面三個備用元件放置在熱備用模式中,，后面三個備用元件放置在冷備用模式中,，那么根據(jù)前面的估算方法就能夠得出系統(tǒng)的任務(wù)成本開銷C=21 476和可靠性R=0.956 2。

　　接下來研究時間單元m對系統(tǒng)可靠性和預期成本的影響,，將三個備用元件放置在熱備用模式下,，其余三個備用元件放置在冷備用模式下，根據(jù)圖2能夠得出不同時間單元對可靠性和預期成本的影響,。

　　3.2元件最優(yōu)分布與初始化順序

　　設(shè)定有8個備用元件存在于系統(tǒng)中,，根據(jù)表1提供的各種參數(shù)以及模型中的可靠性與成本估算方法，采用蟻群遺傳混合算法進行優(yōu)化處理,，能夠獲得系統(tǒng)中備用元件的最優(yōu)序列分布,，并且隨著遺傳迭代的改變，最優(yōu)解越來越趨于穩(wěn)定,，如圖3所示,。

　　同時能夠求出在達到不同的可靠性級別R*的時候，設(shè)置蟻群算法初始值信息素τc為20,，遺傳算法進入到蟻群算法的信息素強度值τg為2,，螞蟻數(shù)量為6，采用蟻群遺傳算法得出復雜系統(tǒng)的可靠性和預期任務(wù)成本以及備用元件的初始化序列,，如表2所示,。　

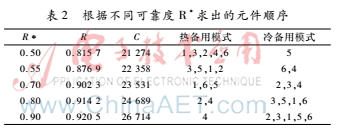
　　最后得出不同的可靠性與預期任務(wù)成本的一個平衡趨勢曲線,，如圖4所示,。這種平衡趨勢曲線能夠協(xié)助復雜系統(tǒng)的混合冗余備用模型的設(shè)計，并且可依據(jù)對成本和可靠性的需要來分配備用元件。

4結(jié)論

　　本文針對系統(tǒng)中工作的元件遇到故障不可修復的情況,，設(shè)計了一種混合冗余備用模型,，根據(jù)概率分布的計算方法，通過仿真實驗來計算得出混合備用模式下系統(tǒng)的可靠性和預期運行成本,，提出了基于蟻群遺傳混合算法對系統(tǒng)中冗余備用元件的分布進行處理和優(yōu)化的方案,，找到了在滿足一定可靠性和預期任務(wù)成本的條件下，系統(tǒng)中備用元件的一組初始化序列,，為系統(tǒng)元件分布和優(yōu)化提供了依據(jù),。

參考文獻

　　［1］ 劉士喜,許志才,方賢文.基于隨機Petri網(wǎng)的冗余備份系統(tǒng)可信賴性研究［J］.安徽理工大學學報(自然科學版),，2009,29(3):48-53.

　?。?］ 黎邵平,李錫文.雙機熱冗余控制系統(tǒng)的可靠性分析［J］.自動化技術(shù)與應(yīng)用，2006,25(12):18-20.

　?。?］ LEVITIN G,Liu Dongxing,Dai Yuanshun.Reliability and mission cost of 1outof N:G systems with statedependent standby mode transfers［J］.IEEE Transactions on Reliability,2015,64(1):454-462.

　?。?］ 楊博文,趙海,劉飛,等.基于可靠度的導彈維修備件需求評估方法研究［J］.微型機與應(yīng)用,2011,30(4):94-96.

　　［5］ 仲彥軍.冷備狀態(tài)下具有兩個狀態(tài)的由兩個相同部件并聯(lián)的可修系統(tǒng)研究［D］.烏魯木齊：新疆大學,2006.

　?。?］ 馬書南,，帥訓波，曹鳳雪.一種基于逆序算子優(yōu)化組合遺傳算法［J］.電子技術(shù)應(yīng)用,2006,，32（6）：19-21.

　?。?］ 程世娟,盧偉,何平.蟻群算法在冗余系統(tǒng)可靠性最優(yōu)分配上的應(yīng)用［J］.計算機工程與應(yīng)用，2009,，45(15)：64-66.

　?。?］ 申利民.基于遺傳蟻群融合算法的測試用例最小化研究［J］.計算機工程，2012,，38(16):57-64.

　?。?］ 姜封國.基于混合遺傳算法的隨機結(jié)構(gòu)可靠性優(yōu)化設(shè)計［J］.華南理工大學學報,2008，36(1):152-156.

　?。?0］ 徐德明.改進的遺傳混合蟻群算法在TSP問題中的應(yīng)用［J］.計算機時代,，2012(11)：1-64.

　　［11］ 楊劍峰.基于遺傳算法和螞蟻算法求解函數(shù)優(yōu)化問題［J］.浙江大學學報,，2007,41(3): 427-430.