0 引言

    四旋翼飛行器因為其結(jié)構(gòu)簡單對稱、相對容易控制的特點,，在監(jiān)測,、檢查、救援,、電子情報等很多重要的領(lǐng)域被廣泛使用^[1-2],，最近幾年在學(xué)術(shù)界和科研領(lǐng)域引起很大興趣。四軸飛行器姿態(tài)角解算的速度和精度直接影響飛行器是否能獲得實時,、穩(wěn)定的飛行姿態(tài),，所以姿態(tài)解算是四旋翼飛行器研究的核心之一。

    對于四旋翼飛行器的姿態(tài)測量,，采用集成了三軸陀螺儀和三軸加速度計的MPU6050進行姿態(tài)數(shù)據(jù)的采集,，在較簡單的硬件平臺下，應(yīng)該怎樣濾除外部干擾,，得到精確度比較高的數(shù)據(jù)變得十分重要,。近幾年姿態(tài)估計算法隨著電子技術(shù)的發(fā)展相繼出現(xiàn)。文獻(xiàn)[3]應(yīng)用互補濾波^[3]對四旋翼的數(shù)據(jù)進行融合,，該算法可以有效抑制因電機轉(zhuǎn)動而帶來的周期性干擾和因溫度影響給MPU6050帶來的漂移誤差,。但是應(yīng)用互補濾波導(dǎo)致飛控系統(tǒng)有滯后現(xiàn)象，截止頻率附近衰減較慢,，處理后的數(shù)據(jù)存在誤差,，精確度較低,。文獻(xiàn)[4]提出基于歐拉角的迭代擴展卡爾曼^[4]（IEKF）姿態(tài)測量方法，該方法使用歐拉角方法描述姿態(tài)角,，基于EKF濾波算法,，在計算觀測矩陣H時進行多次迭代,，該算法估計出的姿態(tài)比普通EKF估計的姿態(tài)精度高,。但該算法復(fù)雜、計算量大,、循環(huán)周期長,，僅適用于仿真，在實際工程上應(yīng)用較少,。文獻(xiàn)[5-6]提出粒子濾波的算法,，粒子濾波算法是在狀態(tài)空間中尋找一組隨機樣本，近似地表示出概率密度函數(shù),，獲得系統(tǒng)狀態(tài)的最小方差,，當(dāng)樣本數(shù)量趨于無窮時可以逼近任何形式的概率密度函數(shù)，擺脫了解決非線性濾波問題時隨機量必須滿足高斯分布的制約,，因此粒子濾波能夠比較精準(zhǔn)地表達(dá)基于觀測量和控制量的后驗分布,。但是粒子濾波需要大量的樣本數(shù)量才能較準(zhǔn)確地近似系統(tǒng)的后驗概率密度，使得算法復(fù)雜度較高,，而且重采樣階段會造成樣本有效性和多樣性的損失,，導(dǎo)致樣本出現(xiàn)貧化現(xiàn)象。

    利用MPU6050采集姿態(tài)信息,，為了獲得較精確的姿態(tài)角,，對EKF算法進行了改進，MPU6050在每一個采樣時刻可以同時測得當(dāng)前時刻飛行器的姿態(tài)角和姿態(tài)角變化率的信息,，結(jié)合改進EKF算法對數(shù)據(jù)進行處理能夠準(zhǔn)確地估算飛行器當(dāng)前的位置和姿態(tài),。飛行器在飛行過程中受非高斯白噪聲的影響，本文在進行姿態(tài)解算時,，為有效模擬飛行器測量過程的噪聲,，用兩個加權(quán)高斯概率密度函數(shù)表示非高斯白噪聲函數(shù)，選擇合理高斯函數(shù)的權(quán)重,、均值和方差,。通過改進型EKF有效地濾除該噪聲，減小了飛行器姿態(tài)偏差,。

1 系統(tǒng)建模

    為了獲得四旋翼飛行器的姿態(tài)數(shù)據(jù)信息,，首先選定兩個基本坐標(biāo)系：慣性坐標(biāo)系E(XYZ)和機體坐標(biāo)系B(X′Y′Z′)^[7]，如圖1所示,。

式中c代表cos,，s代表sin,，轉(zhuǎn)換矩陣是非線性矩陣，為避免該矩陣出現(xiàn)奇點問題,，飛行器在測試飛行過程中不會做出大幅度機動動作,，因而可以認(rèn)為系統(tǒng)滿足以下假設(shè)：

    (1)四旋翼飛行器橫滾角與俯仰角滿足以下不等式：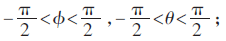

    (2)在實際飛行中飛行器角速度信號由陀螺儀測量，因此可以假設(shè)飛行器橫滾角速度與偏航角速度為有界信號L_∞,，即：w_x∈L_∞,，w_z∈L_∞。

    MPU6050可以快速,、穩(wěn)定地采集飛行器靜止時的姿態(tài)信息,，但當(dāng)飛行器開始運動時，機體抖動及螺旋槳高頻率的運動使得MPU6050測得的飛行器位姿存在明顯的偏差,。利用EKF將MPU6050采集的數(shù)據(jù)進行融合,。EKF濾波原理是將非線性系統(tǒng)進行線性化處理，利用泰勒級數(shù)展開系統(tǒng)函數(shù),，取一次項作為EKF的系數(shù)矩陣,，忽略了高階項噪聲。因此采用EKF進行姿態(tài)解算存在較大的濾波偏差,。針對以上問題,，本文提出改進型EKF，對四旋翼飛行器的姿態(tài)數(shù)據(jù)進行解算,。

2 改進型擴展卡爾曼濾波原理及算法

    為有效濾除噪聲,，測得精確的姿態(tài)數(shù)據(jù)，對EKF濾波算法進行了改進,，采用兩個EKF并行地對四旋翼飛行器的姿態(tài)數(shù)據(jù)進行預(yù)測和更新,，將它們輸出的狀態(tài)變量加權(quán)整合后輸出飛行器的最優(yōu)狀態(tài)估計，因此經(jīng)改進EKF處理后的飛行器姿態(tài)數(shù)據(jù)達(dá)到最小均方誤差,。實現(xiàn)對飛行器位姿的有效操控,，從理論上分析經(jīng)過改進EKF濾波后的效果會更加接近真實值，有效地濾除噪聲,，且算法復(fù)雜度低,、運算量小，不需要時頻域的頻繁轉(zhuǎn)換,，更不會因為樣本數(shù)量的選擇而導(dǎo)致樣本重采樣現(xiàn)象,，融合后飛行器姿態(tài)數(shù)據(jù)精度高。具體步驟如下：

    (1)EKF1 與EKF2 對四旋翼飛行器姿態(tài)數(shù)據(jù)并行地進行處理,，輸出對應(yīng)的狀態(tài)變量X_1,，k、X_2,，k和協(xié)方差P_1,，k,、P_2，k,；

    (2)計算EKF1 和EKF2的似然函數(shù),，求出對應(yīng)的權(quán)重a₁、a₂,；

    (3)加權(quán)整合后更新四旋翼飛行器狀態(tài)X_k和協(xié)方差P_k,，輸出飛行器姿態(tài)的最優(yōu)估計；

    (4)實時調(diào)整飛行器姿態(tài),，待飛行器下一個狀態(tài)到達(dá)前返回步驟(1),，繼續(xù)下一次循環(huán)。

    具體過程如圖2所示,。

    對于一個隨機系統(tǒng)，具體的估計過程如下：

3 仿真與實驗

    在改進型EKF理論的基礎(chǔ)上進行仿真,，在NI my RIO-1900的實驗平臺上對飛行器進行實驗,。

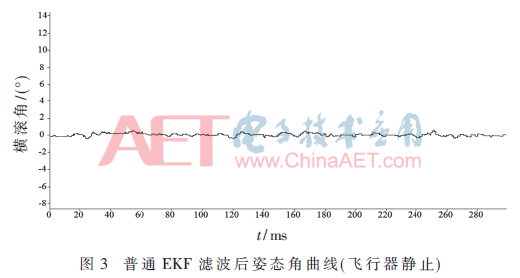
    為保證飛行器初始時刻的穩(wěn)定性及減小初始時刻姿態(tài)誤差，對初始時刻四旋翼飛行器姿態(tài)數(shù)據(jù)進行濾波處理,，以橫滾角為例,，采集飛行器靜止時刻姿態(tài)數(shù)據(jù)，改進EKF濾波后姿態(tài)與普通EKF濾波后姿態(tài)進行對比,，如圖3,、圖4所示。普通EKF濾波后飛行器姿態(tài)有約1°左右的偏差,，改進EKF濾波后飛行器姿態(tài)穩(wěn)定性較好,，偏差較小，幾乎可以忽略,。二者相比較,，改進型EKF的濾波效果較好，魯棒性強,。

    給飛行器橫滾角一個操控命令,，使其傾斜14°，飛行器在執(zhí)行操控命令時,，機體坐標(biāo)系繞慣性坐標(biāo)系旋轉(zhuǎn)會產(chǎn)生一定旋轉(zhuǎn)角,，橫滾角初始狀態(tài)不是絕對的0°，經(jīng)測試飛行器初始時刻橫滾角為0.41°,。如圖5和圖6所示,，飛行器接收到操控命令后，普通EKF濾波后的飛行器經(jīng)40 ms達(dá)到期望姿態(tài),，在140 ms 內(nèi)有波動,，140 ms 之后飛行器波動范圍減小,，但存在約0.5°左右的偏移。改進EKF濾波后的飛行器經(jīng)38 ms后達(dá)到期望姿態(tài),，僅用時80 ms飛行器就達(dá)到理想狀態(tài),，且偏移較小，可以忽略,。從二者的對比圖可得出,，改進型EKF濾波后飛行器姿態(tài)角較穩(wěn)定，提高了系統(tǒng)的準(zhǔn)確性和可靠性,。

    通過MPU6050采集四旋翼飛行器0～100 s內(nèi)的姿態(tài)數(shù)據(jù),，采集的姿態(tài)經(jīng)改進EKF濾波后的動態(tài)測試如圖7，在4 s～16 s,、48 s～54 s,、60 s～70 s、72 s～86 s,、91 s～96 s時間段內(nèi),，改進EKF估計值完全跟蹤到理想值，在16 s～18 s,、23 s～26 s,、56 s～59 s、96 s～99 s時間段內(nèi),，由于四旋翼飛行器姿態(tài)角度變化幅度較大,，改進EKF估計值與理想值之間出現(xiàn)偏差，但在下一刻,，即19 s,、27 s、60 s,、100 s時,，改進EKF估計值快速恢復(fù)實時追蹤。

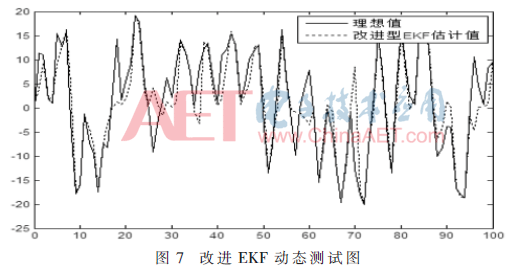
    經(jīng)計算,，改進EKF估計值均方誤差為3.306,，普通EKF估計值均方誤差為5.884 3。改進EKF估計值精度明顯高于普通EKF估計值精度,。精度提高的效率為：

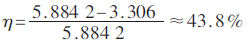
    經(jīng)過多次測試可知：該算法設(shè)計合理,，姿態(tài)精度有較明顯的改善，改進的算法已成功應(yīng)用在四旋翼飛行器上,，得到了理想的效果,。

4 結(jié)論

    本文改進的擴展卡爾曼了濾波算法，克服了非高斯白噪聲對傳感器姿態(tài)解算的影響,，且該算法復(fù)雜度低,、精度高,、計算量小。實驗結(jié)果表明,，改進的算法可以準(zhǔn)確地估計出姿態(tài)角,，與經(jīng)過普通EKF濾波后的姿態(tài)測量值對比，改進EKF在飛行器姿態(tài)精度上有較明顯的改善,，驗證改進方法是有效的,，為四旋翼無人機實時調(diào)整姿態(tài)提供了一種科學(xué)手段。該算法只對MPU6050采集的數(shù)據(jù)進行融合處理,，進一步可將該算法應(yīng)用至地磁計模塊,，對飛行器數(shù)據(jù)進一步進行融合處理，以快速實現(xiàn)飛行器的垂直起飛和懸停的控制操作,。

參考文獻(xiàn)

[1] ROSALES C,，GANDOLFO D，SCAGLIA G,，et al.Trajectory tracking of a mini four-rotor helicopter in dynamic environments-a linear algebra approach[J].Robotica,，2015，33(8)：1628-1652.

[2] LUPASHIN S,，HEHN M，MUELLER M W,，et al.A platform for aerial robotics research and demonstration：the flying machine arena[J].Mechatronics,，2014，24(1)：41-54.

[3] LU X,，LI J,，LIU W.A study of complementary filter algorithm for four-rotor helicopters attitude control system[J].Sensors & Transducers，2014,，174(7)：298-306.

[4] 賀海鵬,，閻妍，馬良,，等.基于IEKF的四旋翼無人機姿態(tài)測量方法研究[J].計算機仿真,，2015(4)：56-60.

[5] MERCADO D A，CASTILLO P,，LOZANO R.Quadrotors data fusion using a particle filter[C].Unmanned Aircraft Systems(ICUAS),，2014 International Conference on.IEEE，2014.

[6] 曲仕茹,，馬志強.改進的粒子濾波在四旋翼姿態(tài)估計中的應(yīng)用[J].飛行力學(xué),，2013(5)：458-461，466.

[7] ZHAO S,，AN H,，LIU J,，et al.Identification of aerodynamic parameter for quadrotor model[J].Journal of Electronic Measurement & Instrument，2013,，27(8)：744-749.

作者信息：

侯玉涵,，王耀力

(太原理工大學(xué) 信息工程學(xué)院，山西 太原030024)