0 引言

    四旋翼飛行器是一種常見的特定配置的垂直起降微型飛行器,，它具有體積小,、靈活性高、機(jī)動(dòng)性強(qiáng)和結(jié)構(gòu)簡單操作方便等優(yōu)點(diǎn),，具有廣闊的應(yīng)用前景^[1],。它是四輸入六輸出的典型欠驅(qū)動(dòng)、強(qiáng)耦合的非線性系統(tǒng),，理論研究表明，用非線性的控制器實(shí)現(xiàn)四旋翼飛行器具有良好的控制效果,。由于物理機(jī)體和數(shù)學(xué)模型之間的差異,，常用PID控制器作為飛行器的控制系統(tǒng)^[2]。然而在實(shí)際應(yīng)用中,，被控對象自身的非線性,、延遲性和滯后性等原因，PID控制器參數(shù)的整定非常困難,。參數(shù)設(shè)置的不理想不但會(huì)影響控制系統(tǒng)的穩(wěn)定性,，而且會(huì)無法完成預(yù)期效果，甚至引發(fā)工業(yè)事故,，因此PID控制參數(shù)自整定對控制系統(tǒng)具有重要作用,。

    按照發(fā)展階段,，自整定分為常規(guī)自整定和智能自整定兩類，常規(guī)PID參數(shù)自整定按其工作機(jī)理分為兩種：基于規(guī)則的自整定方法和基于模式辨識的自整定方法^[3],。

    基于規(guī)則的自整定方法在參數(shù)整定及控制過程方面不需要特定經(jīng)驗(yàn),，還可以將過程特性和干擾特性區(qū)分開，但是需要技術(shù)人員對每一個(gè)回路和控制參數(shù)都有深入和全面的了解,。對于控制系統(tǒng),，要求明確哪個(gè)控制參數(shù)需要調(diào)節(jié)，但是需要調(diào)節(jié)的控制參數(shù)不容易確定,。

    基于模式辨識自整定的方法簡單,、直觀、易實(shí)現(xiàn),，但是在實(shí)際工業(yè)生產(chǎn)過程中,，因其非線性、動(dòng)態(tài)性,、系統(tǒng)的噪聲和結(jié)構(gòu)的復(fù)雜性等特點(diǎn),，該方法并沒有取得預(yù)期的結(jié)果，而且該方法工作量比較大,。

    隨著科技發(fā)展,，智能參數(shù)自整定相繼出現(xiàn)。其中模糊推理整定^[4]不需要精確的數(shù)學(xué)模型,，具有較強(qiáng)的魯棒性,，但是它依賴于確定的PID參數(shù)，屬于一種局部尋優(yōu)算法,；遺傳算法降低了設(shè)計(jì)難度,，具有良好的魯棒性和全局性，但其存在收斂性,、局部搜索能力差等問題,。本文是在智能PID控制的基礎(chǔ)上，提出結(jié)合共軛梯度算法對數(shù)字PID控制參數(shù)進(jìn)行自整定,，將控制性能指標(biāo)的最小方差和控制率相結(jié)合,，根據(jù)梯度算法迭代出被控系統(tǒng)不斷變化的參數(shù)，使PID控制器的效率得以提升,，提高了系統(tǒng)的魯棒特性,、可靠性和準(zhǔn)確性。

1 四旋翼飛行器建模

    四旋翼飛行器是固定在一個(gè)十字交叉的結(jié)構(gòu)上,，由4個(gè)電機(jī)驅(qū)動(dòng)螺旋槳的轉(zhuǎn)動(dòng),，并且通過螺旋槳速度的改變來改變飛行器的姿態(tài)^[5]。其工作原理圖如圖1所示,。

    四旋翼飛行器在全局坐標(biāo)系下沿X,、Y,、Z軸的線位移運(yùn)動(dòng)方程為：

    根據(jù)力矩平衡原理，四旋翼飛行器在全局坐標(biāo)系X,、Y,、Z方向的角位移方程為：

其中，l是四旋翼飛行器重心到螺旋槳的距離,，k_i(i=4,，5，6)是四旋翼飛行器在角位移運(yùn)動(dòng)是的空氣阻力系數(shù),，I是每個(gè)軸上的轉(zhuǎn)動(dòng)慣量M是每個(gè)螺旋槳產(chǎn)生的扭動(dòng)力矩^[6],。

    假定U_i(i=1，2,，3,，4)為四旋翼飛行器控制系統(tǒng)的輸入量，在實(shí)驗(yàn)階段,，四旋翼飛行器處于低速飛行的狀態(tài),，忽略空氣阻力^[7]，將式(1)和式(2)化簡得出系統(tǒng)的數(shù)學(xué)模型：

    四旋翼飛行器是用PID控制器作為控制系統(tǒng),，其控制系統(tǒng)模型如圖2所示,。

    由圖2知四旋翼飛行器的飛行姿態(tài)是由PID控制器通過調(diào)節(jié)4個(gè)電機(jī)的轉(zhuǎn)速來實(shí)現(xiàn)，為了增強(qiáng)四旋翼飛行器飛行姿態(tài)的穩(wěn)定性和可靠性,，對PID控制器進(jìn)行優(yōu)化是必要的,。為此提出了共軛梯度算法對PID控制參數(shù)的自整定，從而使控制系統(tǒng)輸出達(dá)到最優(yōu),。

2 共軛梯度算法對PID參數(shù)的整定

    在四旋翼飛行器數(shù)學(xué)模型的基礎(chǔ)上,，根據(jù)PID控制系統(tǒng)的輸出u(k)和整個(gè)系統(tǒng)的輸出y(k)組成數(shù)據(jù)序列，在設(shè)計(jì)過程中引入?yún)?shù)γ,，通過對γ不斷進(jìn)行迭代估計(jì),，得出k時(shí)刻的參數(shù)估計(jì)值利用最小方差控制率計(jì)算出并以此改善調(diào)節(jié)器的參數(shù)，調(diào)節(jié)器在新參數(shù)條件下對過程進(jìn)行控制,。通過不斷對參數(shù)的迭代估計(jì),，直到其收斂到真值，即調(diào)節(jié)器對過程的控制達(dá)到最小方差控制時(shí),，參數(shù)就能夠使控制過程達(dá)到最優(yōu),。

    根據(jù)位置式PID控制器^[8]得到：

    由式(4)遞推出增量式PID控制^[9]的公式：

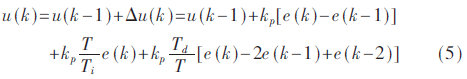
    然后引入共軛梯度算法,，設(shè)目標(biāo)函數(shù)為：

其中,，y₀為理想值，y(k-j)為(k-j)時(shí)刻的輸出值,，γ是含控制參數(shù)k_p,、T_i,、T_d的向量。

    在優(yōu)化值附近可將式(6)簡化為：

    利用梯度算法求解γ的最優(yōu)估計(jì),，則迭代公式為：

    不同的PID控制器對應(yīng)著不同的γ,，因此設(shè)定系統(tǒng)的輸出為：

3 仿真分析

    將共軛梯度算法對PID參數(shù)的自整定和四旋翼飛行器的數(shù)學(xué)模型相結(jié)合，在以NI-myrio為控制核心的四旋翼飛行器上利用LabVIEW編程進(jìn)行仿真,，通過MPU6050采集四旋翼飛行器俯仰角,、橫滾角、偏航角的數(shù)據(jù),，利用普通PID控制采集的數(shù)據(jù)與其對比,。以橫滾角偏移13°的時(shí)刻恢復(fù)到平穩(wěn)狀態(tài)和在平穩(wěn)狀態(tài)的穩(wěn)定性為例，采集兩種算法在相同條件,、不同時(shí)刻下的波形圖驗(yàn)證該算法的有效性,，其波形如圖3所示。圖3中：曲線1表示四旋翼飛行器橫滾角在共軛梯度算法下PID控制的仿真曲線,；曲線2表示四旋翼飛行器橫滾角在普通PID控制下的仿真曲線,。

    圖中分別采集了共軛梯度算法的PID控制和普通PID控制的四旋翼飛行器橫滾角在0～224 ms、21～245 ms,、30～257 ms時(shí)刻的仿真結(jié)果,。由圖3(a)得到，四旋翼飛行器橫滾角從13°恢復(fù)到平穩(wěn)狀態(tài),，普通PID控制所需時(shí)間約為47.2 ms,，共軛梯度算法的PID控制所需時(shí)間為23.6 ms，通過對比,，共軛梯度算法的PID控制對四旋翼飛行器的橫滾角恢復(fù)到平穩(wěn)狀態(tài)所需時(shí)間時(shí)間較短,，且提高的效率為：

    由圖3(b)、圖3(c)可知,，普通PID控制的飛行器恢復(fù)到平穩(wěn)狀態(tài)后依然有較大抖動(dòng),，其穩(wěn)定性較差，而共軛梯度算法的PID控制在四旋翼飛行器橫滾角恢復(fù)到平穩(wěn)狀態(tài)后比較穩(wěn)定,，其魯棒性增強(qiáng),，誤差較小。

    通過圖3(c)看出,，普通PID控制的飛行器平穩(wěn)狀態(tài)存在0.5°的偏差,，而共軛梯度算法的PID控制實(shí)現(xiàn)了飛行器無偏移的平穩(wěn)狀態(tài)，提高了系統(tǒng)的準(zhǔn)確性和可靠性,。

    該算法已成功應(yīng)用在四旋翼飛行器,，在實(shí)際飛行中已達(dá)到良好的控制飛行效果，其仿真飛行如圖4所示,。

4 結(jié)論

    本文采用共軛梯度算法對數(shù)字PID控制的參數(shù)進(jìn)行自整定,，將控制性能指標(biāo)的最小方差和控制率相結(jié)合,，根據(jù)梯度算法迭代計(jì)算出被控系統(tǒng)特性不斷變化的控制參數(shù)，在NI-myrio為核心控制的四旋翼飛行器上通過LabVIEW實(shí)現(xiàn)了仿真,。經(jīng)實(shí)驗(yàn)證明,，從飛行的某一狀態(tài)恢復(fù)到穩(wěn)定的時(shí)間明顯縮短，速率明顯提高,，穩(wěn)定性較好,，波動(dòng)較小，取得了較為理想的效果,。該方法只是完成了PID自整定的基本整定功能,，還有許多功能，如增加對多點(diǎn)的自整定功能,、考慮實(shí)際應(yīng)用環(huán)境的多樣性等需進(jìn)一步做實(shí)驗(yàn)驗(yàn)證,。

參考文獻(xiàn)

[1] 姜成平.一種四旋翼無人機(jī)控制系統(tǒng)的設(shè)計(jì)與實(shí)現(xiàn)研究[D].哈爾濱：哈爾濱工業(yè)大學(xué)，2014.

[2] BOUABDALLAH S,，NOTH A,，SIEGWART R.PID vs LQ control techniques applied to an indoor micro quadrotor [C].IEEE，2004：2451-2456.

[3] 周偉.PID參數(shù)自整定的研究與應(yīng)用[D].武漢：華中科技大學(xué),，2011. 

[4] 邊麗華.PID控制器參數(shù)自整定方法的研究與實(shí)現(xiàn)[D].大連：大連理工大學(xué),，2009.

[5] Tao Jili，Lu Wuyi,，Xiong Hongyun.The self-tuning of PID parameters based on advanced genetic algorithm[J].Industrial Instrumentation & Automation,，2004(2).

[6] 尚昱星.光電式動(dòng)態(tài)扭矩測量系統(tǒng)的研究與設(shè)計(jì)[D].秦皇島：燕山大學(xué)，2009.

[7] MADANI T,，BENALLEGUE A.Backstepping control for a quadrotor helicopter[C].IEEE/RSJ International Conference on Intelligent Robots and Systems,，2006：3255-3260.

[8] 段國強(qiáng).四旋翼無人直升機(jī)仿真及控制方法比較研究[D].哈爾濱：哈爾濱工業(yè)大學(xué)，2013.

[9] 宿敬亞,，樊鵬輝,，蔡開元.四旋翼飛行器的非線性PID姿態(tài)控制[J].北京航空航天大學(xué)學(xué)報(bào)，2011(9)：1054-1058.

作者信息:

李  航,，王耀力

(太原理工大學(xué) 信息工程學(xué)院,，山西 太原030024)