《電子技術(shù)應(yīng)用》
您所在的位置：首頁(yè) > 測(cè)試測(cè)量 > 設(shè)計(jì)應(yīng)用 > 概率神經(jīng)網(wǎng)絡(luò)多模型卡爾曼濾波定位導(dǎo)航算法
概率神經(jīng)網(wǎng)絡(luò)多模型卡爾曼濾波定位導(dǎo)航算法
2018年電子技術(shù)應(yīng)用第6期
梁龍凱1，2,，張麗英1，何文超1,，2,，呂緒浩1，2
1.東北師范大學(xué) 人文學(xué)院 理工學(xué)院 汽車(chē)電子與服務(wù)工程系,，吉林 長(zhǎng)春130117,； 2.吉林省高校汽車(chē)電子技術(shù)工程研究中心，吉林 長(zhǎng)春130117
摘要： 交互式多模型擴(kuò)展卡爾曼濾波（IMM-EKF）算法是解決機(jī)動(dòng)載體運(yùn)動(dòng)模型不確定的定位問(wèn)題的次優(yōu)算法,，在載體做模型確定的運(yùn)動(dòng)時(shí)該方法仍得到次優(yōu)解且浪費(fèi)運(yùn)算資源,。針對(duì)IMM-EKF算法的此類(lèi)缺陷，采用離線訓(xùn)練的概率神經(jīng)網(wǎng)絡(luò)模型,，實(shí)時(shí)判斷當(dāng)前運(yùn)動(dòng)模型分類(lèi),，在運(yùn)動(dòng)模型確定的狀態(tài)下選擇對(duì)應(yīng)的單一模型進(jìn)行運(yùn)算，而在運(yùn)動(dòng)模型不確定的狀態(tài)下選擇IMM-EKF算法,，既保證定位精度,，又減少了不必要的運(yùn)算量。仿真對(duì)比實(shí)驗(yàn)驗(yàn)證了相比于IMM-EKF算法,，新算法在精度方面的優(yōu)勢(shì),。
中圖分類(lèi)號(hào)： TP29
文獻(xiàn)標(biāo)識(shí)碼： A
DOI：10.16157/j.issn.0258-7998.174938
中文引用格式： 梁龍凱，張麗英,，何文超,，等. 概率神經(jīng)網(wǎng)絡(luò)多模型卡爾曼濾波定位導(dǎo)航算法[J].電子技術(shù)應(yīng)用,，2018，44(6)：60-62,，67.
英文引用格式： Liang Longkai,，Zhang Liying，He Wenchao,，et al. Probabilistic neural network multi-model Kalman filter navigation algorithm[J]. Application of Electronic Technique,，2018，44(6)：60-62,，67.
Probabilistic neural network multi-model Kalman filter navigation algorithm
Liang Longkai1,，2，Zhang Liying1,，He Wenchao1,，2，Lv Xuhao1,，2
1.Automotive Electronics and Services Engineering Department,，College of Humanities & Sciences of Northeast Normal University， Changchun 130117,，China,； 2.Jilin Provincial University Automotive Electronic Technology Engineering Research Center，Changchun 130117,，China
Abstract： Interacting multiple model extended Kalman filter(IMM-EKF) algorithm is a sub-optimal algorithm which can solve the positioning problem in which the motion model is uncertain. But this method still gets sub-optimal solution and wastes computational resources when the carrier does the motion of which the model is certain. Aiming at this kind of defects of IMM-EKF, the off-line training probabilistic neural network model is adopted to judge the classification of current motion model in real time. We choose to operate with the single corresponding model when the motion model is in the state of certainty, and choose the IMM-EKF algorithm when the motion model is in the uncertain state. Thus it not only ensures the positioning accuracy, but also reduces the unnecessary computation burden. Simulation experiments verify the validity and accuracy of the algorithm, while the contrast test verifies the advantages in accuracy of the new algorithm compared with IMM-EKF algorithm.
Key words : navigation,；extend Kalman filter(EKF)；probabilistic neural network(PNN),；BDS,；GPS

0 引言

    擴(kuò)展卡爾曼濾波(Extend Kalman Filter，EKF)需要一個(gè)準(zhǔn)確的運(yùn)動(dòng)模型,，如果運(yùn)動(dòng)載體的運(yùn)動(dòng)狀態(tài)不確定,，則擴(kuò)展卡爾曼濾波的估計(jì)偏差將會(huì)很大甚至估計(jì)失敗。針對(duì)這種模型不確定的情況,，BLOM H和BAR-SHALOM Y于1988年提出了交互式多模型(Interacting Multiple Model,，IMM)的次優(yōu)算法[1]。因此采用交互式多模型擴(kuò)展卡爾曼濾波(Interacting Multiple Model- Extend Kalman Filter,，IMM-EKF)算法可實(shí)現(xiàn)運(yùn)動(dòng)模型不確定的非線性系統(tǒng)運(yùn)動(dòng)載體的衛(wèi)星定位,。

    然而IMM-EKF在計(jì)算過(guò)程中需要計(jì)算模型集中所有模型的卡爾曼濾波結(jié)果，運(yùn)算量隨模型集規(guī)模增加[2],，即使在運(yùn)動(dòng)載體的運(yùn)動(dòng)狀態(tài)符合模型集中的某一模型的情況下,，依然要進(jìn)行其他模型的計(jì)算,，且得到次優(yōu)的估計(jì)結(jié)果[3],。

    針對(duì)上述不足,，本文引入概率神經(jīng)網(wǎng)絡(luò)(PNN)算法，通過(guò)離線訓(xùn)練好的神經(jīng)網(wǎng)絡(luò)模型對(duì)運(yùn)動(dòng)狀態(tài)進(jìn)行分類(lèi),，若運(yùn)動(dòng)狀態(tài)與模型集中某模型類(lèi)型匹配,，則采用單一模型進(jìn)行EKF得到最優(yōu)估計(jì)；若運(yùn)動(dòng)狀態(tài)與模型集中任何模型分類(lèi)都不匹配,，則采用IMM-EKF定位,。

1 擴(kuò)展卡爾曼濾波（EKF）

    離散非線性系統(tǒng)的狀態(tài)空間描述為[4]：

ck3-gs1-7.gif

2 GPS/BDS系統(tǒng)濾波模型的建立

    選取GPS/BDS系統(tǒng)的狀態(tài)變量為[5]：

ck3-gs8-9.gif

式中Wk-1為k-1時(shí)刻的系統(tǒng)過(guò)程噪聲，是零均值的高斯白噪聲[6],。式中Φ的具體表達(dá)形式取決于運(yùn)動(dòng)模型的形式[7],，運(yùn)動(dòng)模型可參考文獻(xiàn)[5]和[7]中提到的模型。

3 交互式多模型卡爾曼濾波

ck3-gs10.gif

    ck3-gs11.gif

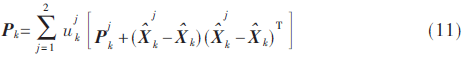
4 引入反饋的概率神經(jīng)網(wǎng)絡(luò)（BP-PNN）

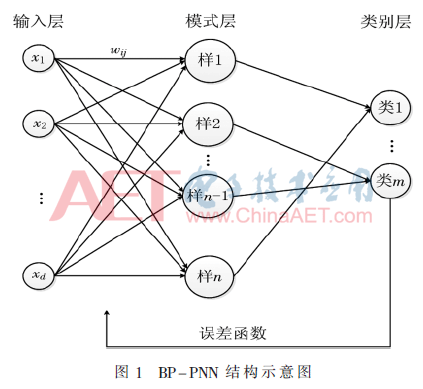
    概率神經(jīng)網(wǎng)絡(luò)是由SPECHT D F于1990年提出的,，用于解決模式分類(lèi)及決策問(wèn)題[8],。李永立等人在此基礎(chǔ)上提出了引入反向傳播機(jī)制的概率神經(jīng)網(wǎng)絡(luò)[9]，使概率神經(jīng)網(wǎng)絡(luò)模型的空間開(kāi)銷(xiāo)減小,，分類(lèi)精度提高,。BP-PNN結(jié)構(gòu)如圖1所示，算法如下,。

ck3-t1.gif

ck3-gs12-17.gif

5 仿真

    運(yùn)動(dòng)軌跡分4個(gè)階段,，分別采用不同的運(yùn)動(dòng)狀態(tài)，各運(yùn)動(dòng)狀態(tài)可遵循不同的狀態(tài)模型,，具體運(yùn)動(dòng)軌跡如表1所示,。

ck3-b1.gif

5.1 實(shí)驗(yàn)1：概率神經(jīng)網(wǎng)絡(luò)的離線學(xué)習(xí)、訓(xùn)練

    在表1的數(shù)據(jù)中分別提取第一階段“勻速轉(zhuǎn)彎”前3 s的數(shù)據(jù)和第三階段“勻加速直線”前3 s的數(shù)據(jù),，將第一階段數(shù)據(jù)目標(biāo)歸類(lèi)定義為1,；將第三階段數(shù)據(jù)目標(biāo)歸類(lèi)定義為2；其他兩個(gè)階段各提取前3 s數(shù)據(jù),，目標(biāo)歸類(lèi)定義為3,。利用各階段前3 s的數(shù)據(jù)進(jìn)行概率神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)，再利用各階段4～6 s數(shù)據(jù)進(jìn)行概率神經(jīng)網(wǎng)絡(luò)訓(xùn)練,。采用任意軌跡數(shù)據(jù)進(jìn)行測(cè)試,，仿真結(jié)果顯示如表2所示。

ck3-b2.gif

    實(shí)驗(yàn)結(jié)果表明經(jīng)過(guò)概率神經(jīng)網(wǎng)絡(luò)的離線訓(xùn)練,，可以比較精確地對(duì)輸入數(shù)據(jù)進(jìn)行分類(lèi),，尤其是勻加速直線運(yùn)動(dòng)的分類(lèi)準(zhǔn)確率最高。

5.2 實(shí)驗(yàn)2：PNN-EKF的準(zhǔn)確性實(shí)驗(yàn)

ck3-5.2-x1.gif

    仿真結(jié)果如圖2所示,。

ck3-t2.gif

    從仿真結(jié)果可以看出PNN-EKF的定位精度要高于IMM-EKF,，但在x軸方向起始階段由于概率神經(jīng)網(wǎng)絡(luò)對(duì)狀態(tài)判斷不準(zhǔn)確造成一定程度的偏差，后續(xù)階段及y軸整體精度都優(yōu)于IMM-EKF。

6 結(jié)束語(yǔ)

    本文提出一種利用概率神經(jīng)網(wǎng)絡(luò)判斷運(yùn)動(dòng)狀態(tài),進(jìn)而采用對(duì)應(yīng)模型進(jìn)行EKF的GPS/BDS導(dǎo)航定位算法,。該算法當(dāng)概率神經(jīng)網(wǎng)絡(luò)能夠判斷其對(duì)應(yīng)運(yùn)動(dòng)模型時(shí),，采用單一模型進(jìn)行最優(yōu)解計(jì)算，如不能判斷準(zhǔn)確模型則歸類(lèi)為“其他”,，“其他”類(lèi)的數(shù)據(jù)采用IMM-EKF算法,。這樣就可以在多數(shù)情況下求得最優(yōu)解，從而提高精度,。通過(guò)仿真實(shí)驗(yàn)證明相較于IMM-EKF,，本文算法定位精度有所提高，從理論推導(dǎo)中可以判斷本文算法當(dāng)模型集較大時(shí)運(yùn)算時(shí)間會(huì)有所減少,。

參考文獻(xiàn)

[1] 翟岱亮,，雷虎民，李炯,，等.基于自適應(yīng)IMM的高超聲速飛行器軌跡預(yù)測(cè)[J].航空學(xué)報(bào),，2016，37(11)：3466-3475.

[2] 董寧,，徐玉嬌,，劉向東.一種帶自適應(yīng)因子的IMM-UKF的GPS/DB-2導(dǎo)航方[J].宇航學(xué)報(bào)，2015,，36（6）：676-683.

[3] 苗少帥,，周峰.IMM迭代無(wú)跡Kalman粒子濾波目標(biāo)跟蹤算法[J].重慶郵電大學(xué)學(xué)報(bào)(自然科學(xué)版)，2015,，27(1)：44-48.

[4] 吳甜甜,，張?jiān)疲瑒⒂烂?，?北斗/GPS組合定位方法[J].遙感學(xué)報(bào),，2014，18(5)：1087-1097.

[5] 徐玉嬌.GPS/BD-2組合導(dǎo)航系統(tǒng)定位算法的研究[D].北京：北京理工大學(xué),，2015.

[6] MONTENBRUCK O,，HAUSCHILD A，STEIGENBERGER P,，et al.Initial assessment of the COMPASS/BeiDou-2 regional navigation satellite system[J].GPS Solutions,，2013，17(2)：211-222.

[7] ZHOU H R,，KUMAR K S P.A ‘current’ statistical model and adaptive algorithm for estimating maneuvering targets[J].Journal of Guidance,，Control，and Dynamics,，1984,，7(5)：596-602.

[8] SPECHT D F.Probabilistic neural networks[J].Neural Networks,，1990，3(1)：109-118.

[9] 李永立,，吳沖,，羅鵬.引入反向傳播機(jī)制的概率神經(jīng)網(wǎng)絡(luò)模型[J].系統(tǒng)工程理論與實(shí)踐，2014,，34（11）：2921-2928.

[10] 苑津莎,，尚海昆.基于主成分分析和概率神經(jīng)網(wǎng)絡(luò)的變壓器局部放電模式識(shí)別[J].電力自動(dòng)化設(shè)備,，2013,，33(6)：27-31.

[11] MICHAEL R B，JAY D.Constructive training of probabilistic neural networks[J].Neurocomputing,，1998,，19(1-3)：167-183.



作者信息:

梁龍凱1，2,，張麗英1,，何文超1，2,，呂緒浩1,，2

（1.東北師范大學(xué) 人文學(xué)院 理工學(xué)院 汽車(chē)電子與服務(wù)工程系，吉林 長(zhǎng)春130117,；

2.吉林省高校汽車(chē)電子技術(shù)工程研究中心,，吉林 長(zhǎng)春130117）

此內(nèi)容為AET網(wǎng)站原創(chuàng)，未經(jīng)授權(quán)禁止轉(zhuǎn)載,。