文獻(xiàn)標(biāo)識(shí)碼: A
DOI:10.16157/j.issn.0258-7998.190457
中文引用格式: 肖宇彤,周淵平,肖駿,等. 子陣級(jí)LCMV循環(huán)優(yōu)化自適應(yīng)波束形成算法研究[J].電子技術(shù)應(yīng)用,2019,45(7):67-71.
英文引用格式: Xiao Yutong,Zhou Yuanping,Xiao Jun,et al. Research on sub-array LCMV cyclic optimization adaptive beamforming algorithm[J]. Application of Electronic Technique,2019,45(7):67-71.
0 引言
自適應(yīng)波束形成是自適應(yīng)陣列信號(hào)處理的重要分支,廣泛應(yīng)用于無(wú)線通信、雷達(dá)、語(yǔ)音信號(hào)處理等領(lǐng)域[1]。自適應(yīng)波束形成問(wèn)題是在某一準(zhǔn)則下尋求最優(yōu)權(quán)矢量,其中包括最小均方(Minimum Mean Squared Error,MMSE)準(zhǔn)則、最大信干噪比(Maximum Signal to Interference and Noise Ratio,MSINR)準(zhǔn)則、最小噪聲方差(Minimum Noise Variance,MNV)準(zhǔn)則[2]。線性約束最小方差(Linearly Constrained Minimum Variance,LCMV)波束形成器是基于MNV的自適應(yīng)波束形成算法,它在最小方差無(wú)失真響應(yīng)(Minimum Variance Distortionless Response,MVDR)濾波器的基礎(chǔ)上引入了線性約束[3]。但在實(shí)際應(yīng)用中,陣列的陣元數(shù)目通常十分龐大,如果使用傳統(tǒng)的LCMV算法,全維矩陣求逆的運(yùn)算量將會(huì)變得極其復(fù)雜,并且收斂性很差,在工程中難以應(yīng)用。因此,研究降維方法不僅對(duì)理論的發(fā)展有重要意義,而且對(duì)工程實(shí)踐也有重要意義[4]。
本文提出的子陣級(jí)LCMV循環(huán)優(yōu)化算法首先對(duì)全維陣列進(jìn)行抽取,形成一組大小不同的子陣列,每組子陣采用相同的權(quán)值。在此基礎(chǔ)上,再對(duì)子陣列進(jìn)行分塊處理,利用循環(huán)迭代的思想對(duì)權(quán)向量進(jìn)行分塊循環(huán)優(yōu)化使其達(dá)到收斂。實(shí)驗(yàn)結(jié)果表明,該方法在大規(guī)模陣列波束形成時(shí)相較于傳統(tǒng)LCMV方法能夠獲得更高的信干噪比(Signal to Interference and Noise Ratio,SINR),相較于子陣級(jí)LCMV算法能夠在達(dá)到收斂的基礎(chǔ)上進(jìn)一步減小求逆矩陣的維數(shù),降低計(jì)算復(fù)雜度及硬件成本。
1 LCMV算法
假設(shè)一個(gè)M陣元的陣列,X(n)是n時(shí)刻M×1維的輸入信號(hào)向量,C是M×L維的約束矩陣,f是L×1維的約束向量。LCMV算法描述如下:

2 部分自適應(yīng)陣列處理——子陣級(jí)LCMV算法
子陣空間部分自適應(yīng)陣的結(jié)構(gòu)如圖1所示,它是將整個(gè)陣列劃分為若干個(gè)子陣列,每個(gè)子陣采用相同的權(quán)值進(jìn)行波束形成[5]。
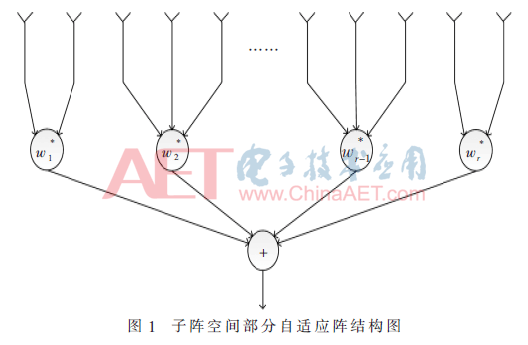
對(duì)M陣元均勻線陣進(jìn)行抽取形成r個(gè)子陣,定義降維矩陣T為:

式中,CT=THC是降維后的約束矩陣,維度為r×L。WT是降維權(quán)向量,由于將全陣列抽取為了r個(gè)子陣,每個(gè)子陣中的陣元共用同一個(gè)權(quán)值,因此WT的維數(shù)為r×1。
3 子陣級(jí)LCMV循環(huán)優(yōu)化算法
將陣列降維輸入信號(hào)XT(n)分塊為:

式中:
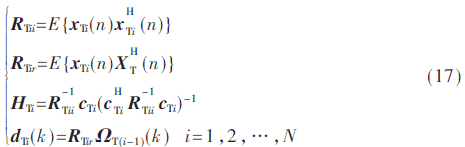
其中,RTii是降維輸入信號(hào)向量分塊xTi(n)的自相關(guān)矩陣。
綜上,子陣級(jí)LCMV循環(huán)優(yōu)化算法在處理大規(guī)模陣列波束形成時(shí)的過(guò)程如下:

4 仿真分析
4.1 實(shí)驗(yàn)1
采用均勻線陣,陣元個(gè)數(shù)為60,陣元之間的間距為半波長(zhǎng),即d=2/λ。采用子陣級(jí)陣列劃分,將60個(gè)陣元不規(guī)則劃分為12組,每組的陣元個(gè)數(shù)依次為:10、6、5、4、4、1、1、4、4、5、6、10。期望信號(hào)從0°方向入射,干擾方向?yàn)?30°、40°、70°。初始信噪比為10 dB,初始干噪比為10 dB,選取的快拍數(shù)為10 000,子陣循環(huán)時(shí)每個(gè)分塊大小為2。按照上述參數(shù)設(shè)置,理想情況下信干噪比SINR=27.781 5 dB。
圖2所示是使用LCMV算法形成的波束圖,信干噪比SINR=20.868 2 dB。
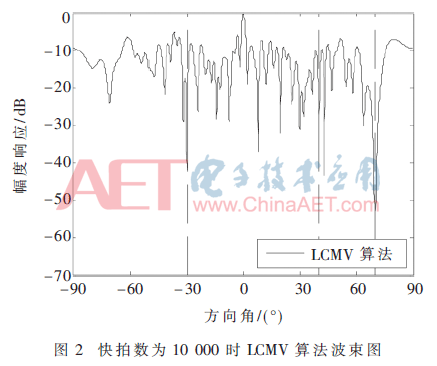
圖3虛線所示是子陣級(jí)LCMV算法形成的波束圖,信干噪比SINR=26.210 5 dB;實(shí)線所示是子陣級(jí)LCMV循環(huán)優(yōu)化算法形成的波束圖, 信干噪比SINR=26.317 0 dB。
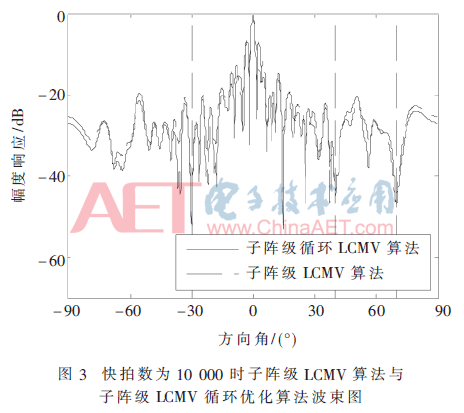
圖4是子陣級(jí)循環(huán)優(yōu)化的信干噪比收斂曲線圖,經(jīng)過(guò)170次循環(huán)迭代后權(quán)值得到收斂。
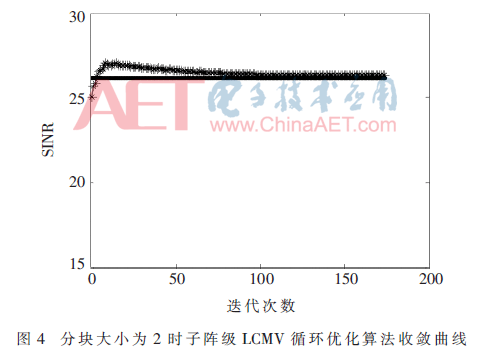
由圖2~圖4可知,在大規(guī)模陣列中,使用LCMV算法得到的波束并不是最佳:收斂性差,旁瓣效應(yīng)顯著且運(yùn)算量巨大。使用子陣級(jí)LCMV算法形成波束時(shí)比LCMV算法的SINR高出了約5 dB,干擾得到了有效抑制,且大幅度降低了波束的旁瓣。子陣級(jí)LCMV循環(huán)優(yōu)化算法通過(guò)循環(huán)迭代,波束的SINR收斂于子陣級(jí)LCMV算法的SINR,且將輸入信號(hào)自相關(guān)矩陣的維度從60×60降低到2×2。雖然增加了迭代過(guò)程,但是大幅度降低了矩陣求逆的運(yùn)算復(fù)雜度,這在實(shí)際工程應(yīng)用中是可行的[7]。
4.2 實(shí)驗(yàn)2
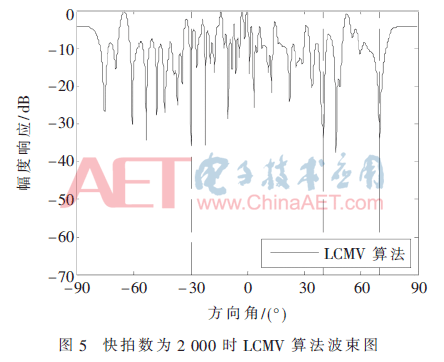
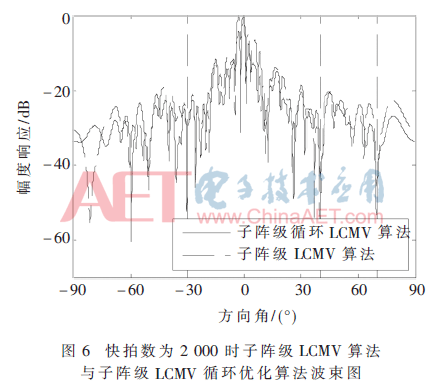
初始參數(shù)保持不變,將快拍數(shù)減小至2 000,3種算法形成的波束圖如圖5、圖6所示。可知當(dāng)快拍數(shù)減小時(shí),LCMV算法已經(jīng)無(wú)法形成性能良好的波束了,而子陣級(jí)LCMV算法與子陣級(jí)LCMV循環(huán)優(yōu)化算法能夠維持良好的性能,二者的SINR分別為23.639 1 dB、25.482 0 dB。這說(shuō)明本文所提出的算法能很好地適用于短快拍的應(yīng)用場(chǎng)景。
4.3 實(shí)驗(yàn)3
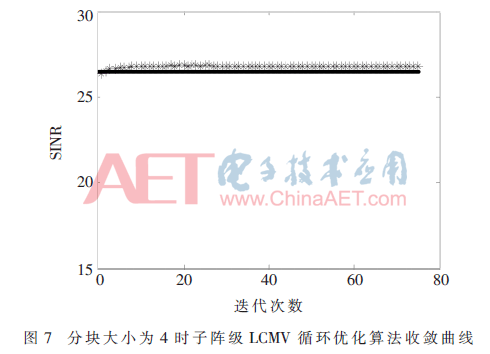
保持實(shí)驗(yàn)1中初始參數(shù)不變,將分塊的大小從2變?yōu)?,子陣級(jí)LCMV循環(huán)優(yōu)化算法收斂曲線如圖7所示。可知,隨著分塊大小的增加,迭代次數(shù)是在不斷減小的。
4.4 實(shí)驗(yàn)4
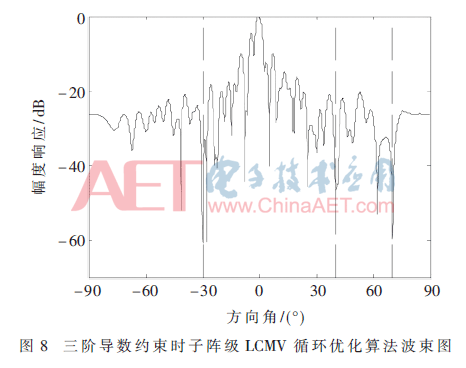
為了拓寬主瓣寬度以增加波束的穩(wěn)健性,在實(shí)驗(yàn)1基礎(chǔ)上加入高階導(dǎo)數(shù)約束[8]。圖8所示為加入三階導(dǎo)數(shù)約束時(shí),主瓣寬度相較于圖3不施加約束時(shí)得到了一定展寬,信干噪比為24.175 9 dB。
4.5 實(shí)驗(yàn)5
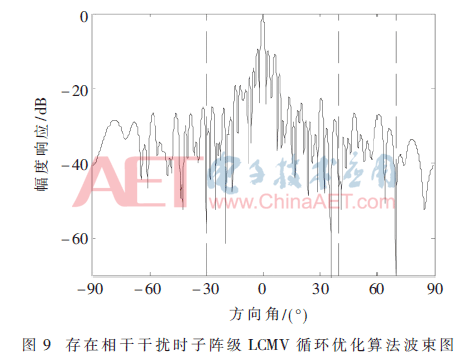
由于在信號(hào)傳輸過(guò)程中存在多徑,多徑在波束形成中屬于相干干擾的一種[9]。此處對(duì)子陣級(jí)LCMV循環(huán)優(yōu)化算法的相干干擾抑制進(jìn)行研究。保持實(shí)驗(yàn)1中的初始參數(shù)不變,將-30°方向處的非相干干擾變?yōu)橄喔筛蓴_,在約束矩陣C中施加相干干擾方向的零點(diǎn)約束,實(shí)驗(yàn)結(jié)果如圖9所示。此時(shí)在相干干擾方向形成了很深的零陷,且信干噪比維持在26.997 6 dB。該方法雖然犧牲了一個(gè)自由度,但保證了期望信號(hào)不會(huì)因相干干擾的存在而被對(duì)消。
5 結(jié)論
針對(duì)大規(guī)模陣列波束形成問(wèn)題,本文提出了子陣級(jí)LCMV循環(huán)優(yōu)化算法,能夠很大程度地降低求逆矩陣的維度,避免了全維矩陣求逆的復(fù)雜性。通過(guò)實(shí)驗(yàn)結(jié)果分析,該算法能夠在降低維度的同時(shí),形成性能良好的波束,并且在施加導(dǎo)數(shù)約束或存在相干干擾時(shí)依然適用。這在實(shí)際工程應(yīng)用中降低了大規(guī)模相控陣列的計(jì)算復(fù)雜度和硬件復(fù)雜度,具有一定的實(shí)用價(jià)值。
參考文獻(xiàn)
[1] 肖駿,周淵平,肖宇彤.基于CSDM-MIMO系統(tǒng)的虛擬信道估計(jì)與權(quán)值優(yōu)化[J].電子技術(shù)應(yīng)用,2019,45(4):83-86.
[2] 羅俊.認(rèn)知無(wú)線電中基于多天線的信號(hào)處理技術(shù)的研究[D].武漢:華中師范大學(xué),2017.
[3] 徐峰,孫雨澤,楊小鵬,等.MIMO雷達(dá)波束形成的低副瓣LCMV算法[J].信號(hào)處理,2017,33(6):805-810.
[4] YU L,ZHANG X,WEI Y.Adaptive beamforming technique for large-scale arrays with various subarray selections[C].CIE International Conference on Radar.IEEE,2017.
[5] HU X,GUO L,LI S,et al.Improved orthogonal projection adaptive beamforming based on normalization at subarray level[C].IET International Radar Conference 2015.IET,2015.
[6] 王永良,丁前軍,李榮鋒.自適應(yīng)陣列處理[M].北京:清華大學(xué)出版社,2009.
[7] 劉權(quán),周淵平,徐磊,等.波束形成算法研究與改進(jìn)[J].信息技術(shù)與網(wǎng)絡(luò)安全,2018,37(4):92-94,109.
[8] YANG X,SUN Y,LIU Y,et al.Derivative constraint-based householder multistage wiener filter for adaptive beamforming[C].International Radar Conference.IET,2013.
[9] ZHANG L,LIU W.A class of robust adaptive beamforming algorithms for coherent interference suppression[C].Signal Processing Conference.IEEE,2012.
作者信息:
肖宇彤,周淵平,肖 駿,周 鑫
(四川大學(xué) 電子信息學(xué)院,四川 成都610065)

