文獻(xiàn)標(biāo)識碼: A
DOI:10.16157/j.issn.0258-7998.191074
中文引用格式: 胡金艷,宋紹京. VPx幀內(nèi)壓縮的快速算法[J].電子技術(shù)應(yīng)用,2020,46(4):75-78,88.
英文引用格式: Hu Jinyan,Song Shaojing. Fast algorithm for VPx intra-frame compression[J]. Application of Electronic Technique,2020,46(4):75-78,88.
0 引言
目前主流的視頻編碼標(biāo)準(zhǔn)包括3個體系:國際聯(lián)合視頻工作組(Joint Video Team,JVT)的H.26x、國內(nèi)數(shù)字音視頻編解碼技術(shù)標(biāo)準(zhǔn)工作組(Audio Video Coding Standard,AVS)的AVSx和Google公司的VPx[1-4]。其中,VPx編解碼器(COder/DECoder,CODEC)憑借開源和免專利費的優(yōu)勢,在全球范圍內(nèi)各種網(wǎng)絡(luò)瀏覽器的支持率已經(jīng)超過92%[5]。
視頻編碼標(biāo)準(zhǔn)中的幀內(nèi)壓縮是決定最終編碼效率的關(guān)鍵,但由于該過程的算法復(fù)雜度高而導(dǎo)致非常耗時,因此對幀內(nèi)壓縮快速算法的研究顯得尤為必要。近年來這方面的研究主要集中在H.264和H.265/高性能視頻編碼(High Efficiency Video Coding,HEVC)[6-9]。文獻(xiàn)[6]通過統(tǒng)計方法與閾值法,文獻(xiàn)[7]基于紋理方向檢測,文獻(xiàn)[8]利用時間與時空相關(guān)性,分別對HEVC幀內(nèi)預(yù)測進(jìn)行加速,實現(xiàn)將編碼時間減少24~30%。文獻(xiàn)[9]提出梯度法加快確定幀內(nèi)模式,將編碼時間減少15%,再結(jié)合支持向量機(Support Vector Machine,SVM)加快確定HEVC編碼單元劃分,使編碼時間進(jìn)一步減少到50%以上。文獻(xiàn)[10]對HEVC和VP9兩種標(biāo)準(zhǔn)的幀內(nèi)壓縮算法及其對編碼效率的影響進(jìn)行了比較。本文針對VPx的幀內(nèi)壓縮提出了加速算法,并通過實驗驗證了算法的效果。
1 VPx幀內(nèi)壓縮
幀內(nèi)壓縮是基于相鄰像素之間的相關(guān)性,通過當(dāng)前塊的相鄰塊對其進(jìn)行預(yù)測,并對預(yù)測值與實際值之間的殘差進(jìn)行一系列變換、量化和熵編碼,以消除空間冗余達(dá)到壓縮的目的。圖1所示為VPx幀內(nèi)壓縮框圖。VPx幀內(nèi)壓縮以宏塊/超級塊為單位,其中VP8標(biāo)準(zhǔn)的宏塊大小為16×16,VP9標(biāo)準(zhǔn)的超級塊大小為64×64。VP8采用4×4的子塊劃分方式將宏塊劃分為4×4大小的子塊,其變換包括離散余弦變換(Discrete Cosine Transform,DCT)和沃爾什-哈達(dá)瑪變換(Walsh-Hadmard Transform,WHT)。VP9采用四叉樹子塊劃分方式將超級塊劃分為4×4~64×64大小的子塊,其變換包括非對稱離散正弦變換(Asymmetric Discrete Sine Transform,ADST)和DCT。
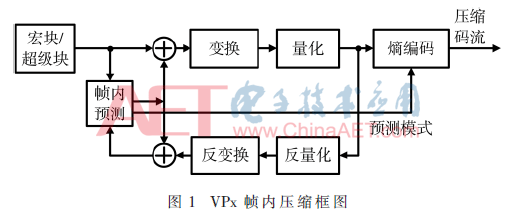
VPx幀內(nèi)預(yù)測分為亮度塊預(yù)測和色度塊預(yù)測。亮度塊預(yù)測包括以下10種預(yù)測模式:

其中,DC和TM分別為直流和真運動預(yù)測模式,另外8種為角度預(yù)測模式,圖2中以4×4的亮度塊預(yù)測為例說明。HE和VE分別為水平和垂直預(yù)測模式,LD和RD分別為45°和135°預(yù)測模式,VL和VR分別為63°和117°預(yù)測模式,HD和HU分別為153°和207°預(yù)測模式。

在幀內(nèi)壓縮過程中,要從上述10種預(yù)測模式中選擇一種,使碼率在不超過某最大碼率的情況下失真最小。VPx采用率失真優(yōu)化(Rate Distortion Optimization,RDO)方法來尋找碼率和失真之間的平衡,其率失真代價函數(shù)表示為:

其中,Jmode為預(yù)測模式對應(yīng)的率失真代價,Dmode為失真,λmode為拉格朗日系數(shù),Bmode為所需比特數(shù)。通過計算預(yù)測殘差的平方和(Sum Squared Error,SSE)得到失真Dmode。對于每個亮度子塊,要進(jìn)行10次變換、量化、反量化和反變換的重構(gòu)過程,根據(jù)率失真代價Jmode最小的原則選取最終預(yù)測模式,進(jìn)入熵編碼。
假設(shè)幀內(nèi)壓縮圖像寬度和高度分別為W和H,宏塊/超級塊大小為C×C,則總的宏塊/超級塊數(shù)為:

以1 280×720的圖像為例,宏塊大小為16×16,按4×4的子塊劃分方式,得到4×4的亮度子塊,則RecCnt的理論值為576 000次,意味著如此大量次數(shù)的變換、量化、反量化、反變換和率失真計算代價。
2 快速算法
為減少幀內(nèi)壓縮的運算量,可以從兩方面入手:一方面減少亮度子塊的重構(gòu)次數(shù),另一方面優(yōu)化幀內(nèi)壓縮的算法程序。下面主要討論前者。
2.1 最近鄰加速法
最近鄰加速法利用當(dāng)前子塊與其最近鄰子塊的相關(guān)性,以最近鄰子塊的預(yù)測模式作為其最終預(yù)測模式,從而減少遍歷預(yù)測模式帶來的重構(gòu)次數(shù)。
圖3所示為將圖像中一個16×16的宏塊劃分為16個4×4的亮度子塊,虛線框表示當(dāng)前子塊,箭頭所在子塊表示其候選最近鄰子塊。

首先根據(jù)當(dāng)前子塊在宏塊中的位置確定最鄰近子塊。設(shè)當(dāng)前子塊為Si,j,3個候選最近鄰子塊分別為Si-1,j、Si,j-1、Si-1,j-1。S1,1作為第一個子塊,不存在最近鄰子塊。
將Si,j的最鄰近子塊定義為NBi,j,當(dāng)候選最近鄰子塊僅存在于水平和垂直方向時,有:
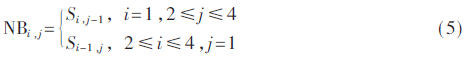
當(dāng)候選最近鄰子塊存在水平、垂直和對角方向時,則先根據(jù)不同方向上子塊的率失真代價從候選最近鄰子塊中確定最近鄰子塊:
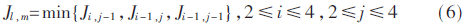
其中,Jl,m為3個方向率失真代價Ji,j-1、Ji-1,j、Ji-1,j-1中最小的,l和m代表最近鄰子塊的坐標(biāo)。則有:

假設(shè)最近鄰子塊NBi,j的最佳預(yù)測模式為mode,對當(dāng)前子塊在該模式下進(jìn)行重構(gòu)和率失真Ji,j計算。當(dāng)滿足如下關(guān)系時,將模式mode作為當(dāng)前子塊的最終預(yù)測模式。

否則將對當(dāng)前子塊進(jìn)行預(yù)測模式的遍歷,得到最終預(yù)測模式。
在最近鄰子塊的判斷過程中,要在當(dāng)前宏塊/超級塊范圍內(nèi),保存當(dāng)前子塊Si,j的前序子塊的最佳預(yù)測模式和與其對應(yīng)的率失真,用于與當(dāng)前子塊直接比較以簡化率失真計算。 2.2 閾值加速法
對當(dāng)前子塊的率失真Ji,j設(shè)置閾值TH。當(dāng)某一預(yù)測模式下的Ji,j滿足如下關(guān)系時,終止對預(yù)測模式的遍歷,將該預(yù)測模式作為當(dāng)前子塊的最終預(yù)測模式:

否則將繼續(xù)進(jìn)行下一個預(yù)測模式。如果所有預(yù)測模式對應(yīng)的率失真均不滿足式(9),則根據(jù)RDO原則選取最佳預(yù)測模式。
閾值的選取直接影響最終結(jié)果。閾值越大,越容易提前終止對預(yù)測模式的遍歷,從而提高壓縮速度,同時降低壓縮質(zhì)量;反之閾值越小,越難滿足閾值要求,遍歷的預(yù)測模式越多,從而保持壓縮質(zhì)量,但壓縮速度提高少。式(10)給出了閾值選取公式:
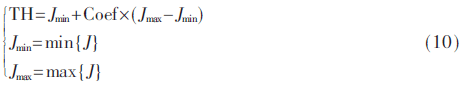
其中,J表示已有子塊率失真的集合,Jmax和Jmin分別為J中的最大率失真和最小率失真,Coef取值0.062 5。
2.3 兩級加速法
采用最近鄰法加速時,如果當(dāng)前子塊存在最近鄰子塊,則能夠減少子塊重構(gòu)運算量;否則仍需要對所有預(yù)測模式進(jìn)行遍歷。采用閾值加速法時,如果當(dāng)前子塊的率失真滿足閾值條件,則能夠減少子塊重構(gòu)運算量;否則仍需要對所有預(yù)測模式進(jìn)行遍歷。
將上述兩種加速方法結(jié)合,構(gòu)成如圖4所示的兩級加速法,使幀內(nèi)壓縮速度進(jìn)一步提高。兩級加速法的第一級為最近鄰加速,第二級為閾值加速。
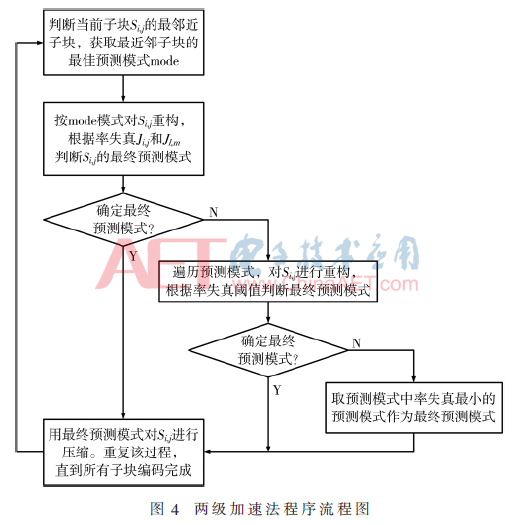
3 實驗結(jié)果與分析
為了驗證算法的有效性,將本文算法在Google官方發(fā)布的libwebp-1.0.0上進(jìn)行實現(xiàn)。該庫利用VP8幀內(nèi)壓縮算法對WebP圖像進(jìn)行編解碼。
實驗的硬件環(huán)境:Inter-CoreTM i5-6200 CPU,主頻為2.40 GHz,內(nèi)存為4.00 GB,操作系統(tǒng)為64 位Windows 10。軟件環(huán)境:Visual C++ 6.0。參數(shù)設(shè)置:品質(zhì)因數(shù)(Quality factor)為80。選用源自Wikipedia的6張測試圖像,如圖5所示。這些圖像涵蓋不同的分辨率和內(nèi)容復(fù)雜度。

對測試圖像分別用原始方法、最近鄰加速法、閾值加速法和兩級加速法進(jìn)行編碼實驗。表1所示為幾種方法對應(yīng)的單張圖像子塊重構(gòu)數(shù)統(tǒng)計。可以看出,采用最近鄰法和閾值法均使子塊重構(gòu)次數(shù)在一定程度上降低。對于圖像Balloon,由于原圖像較平坦,最近鄰法得到的子塊重構(gòu)次數(shù)降低到原重構(gòu)次數(shù)的1/3以下;而對于圖像Boy,原圖像具有較多細(xì)節(jié),最近鄰法得到的子塊重構(gòu)次數(shù)僅有少量降低。結(jié)合閾值法后,對于上述測試圖像,通過兩級法加速后得到的子塊重構(gòu)次數(shù)均大幅度減少。
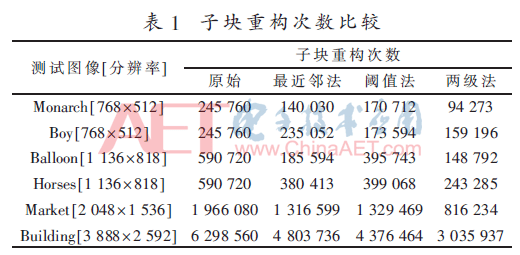
圖6對幾種加速方法從編碼時間T、編碼比特率BR和峰值信噪比PSNR 3個方面進(jìn)行比較。可以看出對分辨率和內(nèi)容不同的圖像,幀內(nèi)編碼的時間都有大幅度降低,而BR和PSNR只有很小的變化。通過式(11)可以進(jìn)一步得到上述算法的具體性能指標(biāo):

其中,ΔT表示所提出算法的編碼時間減少的百分比,Torg和Tproposed分別為原始編碼時間和所提出算法的編碼時間;ΔPSNR表示PSNR減少的dB值,PSNRorg和PSNRproposed分別為原始編碼的PSNR和所提出算法的PSNR;ΔBR表示BR增加的百分比,BRorg和BRproposed分別為原始編碼的BR和所提出算法的BR。根據(jù)對測試圖像的實驗統(tǒng)計和計算結(jié)果,得到最近鄰法的ΔT平均為37%,ΔBR平均為1%,ΔPSNR平均為0.06 dB;兩級法的ΔT平均為49%,ΔBR平均為4%,ΔPSNR平均為0.14 dB。采用兩級法加速時,圖像Balloon加速最多,ΔT達(dá)到59%,對應(yīng)編碼質(zhì)量ΔBR為6%,ΔPSNR為0.24;圖像Boy加速最少,ΔT為41%,對應(yīng)編碼質(zhì)量ΔBR為1%,ΔPSNR為0.07。
4 結(jié)論
為了降低VPx幀內(nèi)壓縮的計算復(fù)雜度,減少編碼時間,本文提出了一種快速算法。實驗結(jié)果表明:對于不同內(nèi)容復(fù)雜度的圖像,所提出的最近鄰法在編碼時間明顯減少平均37%的情況下,對圖像質(zhì)量影響極小;基于最近鄰法進(jìn)一步提出的兩級加速法在對圖像質(zhì)量影響很小的情況下,編碼時間大幅度減少平均49%。進(jìn)一步的優(yōu)化工作包括子塊劃分、幀內(nèi)壓縮算法的軟件優(yōu)化和硬件加速。
參考文獻(xiàn)
[1] SULLIVAN G J,OHM J,HAN W J,et al.Overview of the high efficiency video coding(HEVC) standard [J].IEEE Transactions on Circuits & Systems for Video Technology, 2012, 22(12): 1649-1668.
[2] 黃鐵軍.AVS2標(biāo)準(zhǔn)及未來展望[J].電視技術(shù),2014,38(22):7-10.
[3] BANKOSKI J,WILKINS P,XU Y W.Technical overview of VP8,an open source video codec for the web[C].2011 IEEE International Conference on Multimedia and Expo,ICME′11.IEEE,2011:1-6.
[4] SRINIVASAN M.VP9 Encoder and decoders for next generation online video platforms and services[C].SMPTE 2016 Annual Technical Conference and Exhibition,SMPTE,2016:1-14.
[5] LI Z R,DUANMU ZH F,LIU W T,et al.AVC,HEVC,VP9,AVS2 or AV1?-A comparative study of state-of-the-art video encoders on 4K videos[C].Image Analysis and Recognition ICIAR 2019,Springer,2019,11662:162-173.
[6] 李偉,王讓定,王家驥.一種HEVC幀內(nèi)預(yù)測模式快速選擇算法[J].計算機工程與應(yīng)用,2016,52(14):161-166.
[7] RUIZ D,ESCRIBANO G F,MARTINEZ J L,et al.Fast intra mode decision algorithm based on texture orientation detection in HEVC[J].Signal Processing: Image Communication,2016,44:12-28.
[8] 諶博,顧梅花,馬蒙蒙.一種改進(jìn)的HEVC幀內(nèi)預(yù)測算法[J].計算機與數(shù)字工程,2017,45(1):131-134.
[9] ZHANG T,SUN M T,ZHAO D,et al.Fast intra mode and CU size decision for HEVC[J].IEEE Transactions on Circuits & Systems for Video Technology,2017,27(8):1714-1726.
[10] SHARABAYKO M P,PONOMAREV O G,CHERNYAK R I.Intra compression effciency in VP9 and HEVC[J].Applied Mathematical Sciences, 2013, 7(137): 6803-6824.
作者信息:
胡金艷,宋紹京
(上海第二工業(yè)大學(xué) 計算機與信息工程學(xué)院,上海201209)

