??? 摘 要： 詳細(xì)描述了密度進(jìn)化（DE）方法的基本原理,，比較和分析了離散密度進(jìn)化(DDE),、對(duì)稱(chēng)傅立葉變換" title="傅立葉變換">傅立葉變換(SFT)和高斯" title="高斯">高斯近似(GA)等三種具體算法的特點(diǎn),，并求出AWGN信道下一些度分布的門(mén)限值,。這對(duì)LDPC碼理論分析和應(yīng)用研究具有重要指導(dǎo)作用,。
??? 關(guān)鍵詞： LDPC碼? 密度進(jìn)化? 門(mén)限值
?
??? LDPC碼是Gallager提出的逼近香農(nóng)限的好碼[1],。當(dāng)碼長(zhǎng)較長(zhǎng),、碼型設(shè)計(jì)適當(dāng)時(shí)，其性能甚至優(yōu)于Turbo碼,。Gallager發(fā)現(xiàn)了LDPC碼的門(mén)限現(xiàn)象：若信道噪聲" title="信道噪聲">信道噪聲小于某個(gè)固定的門(mén)限值,，只要碼長(zhǎng)趨于無(wú)窮，則可以達(dá)到任意小的誤碼概率,。Richardson等[3][4]基于消息傳遞機(jī)制的置信傳播(Belief Propagation)譯碼算法提出了密度進(jìn)化分析(Density Evolution)的思想,。通過(guò)跟蹤譯碼器中傳遞消息的概率密度函數(shù)在迭代過(guò)程中的變化情況，分析譯碼收斂特性,，得到特定信道下的門(mén)限值,。對(duì)于研究譯碼過(guò)程和碼的設(shè)計(jì)，密度進(jìn)化是一種非常有用的工具,。
??? 在參考文獻(xiàn)[4]中,，Richardson等給出了密度進(jìn)化的直接算法。這種迭代分析方法非常復(fù)雜,，計(jì)算量巨大,。為此，Sae-Yang Chung[5][7],、Hui Jin[6]等提出了密度進(jìn)化的不同實(shí)現(xiàn)方法,，在計(jì)算精度損失可以接受的情況下,，極大地提高了分析的效率。本文將基于密度進(jìn)化的基本理論,，討論其實(shí)現(xiàn)方法和在門(mén)限判決中的應(yīng)用,。
1 LDPC碼和密度進(jìn)化
??? LDPC碼是具有稀疏奇偶校驗(yàn)矩陣的線性分組碼。一個(gè)LDPC碼集可以由一個(gè)度分布(λ,ρ)確定,，即由變量節(jié)點(diǎn)和校驗(yàn)節(jié)點(diǎn)的度分布函數(shù)確定：
??? 
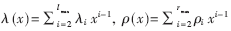
其中l(wèi)max和rmax分別表示變量節(jié)點(diǎn)和校驗(yàn)節(jié)點(diǎn)的最大度數(shù),。規(guī)則碼(dv,dc)是一種特殊情形,，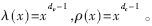
??? LDPC碼最常用的譯碼算法是和積算法(Sum-Product Algorihm),。基于文獻(xiàn)[4]中的無(wú)環(huán)假設(shè),，如果一個(gè)規(guī)則LDPC碼（dv,dc）沒(méi)有長(zhǎng)度小于或等于2l的環(huán),，則在l次迭代內(nèi)，可以假定所有的消息變量是獨(dú)立的,。設(shè)u0表示變量節(jié)點(diǎn)接收信號(hào)的對(duì)數(shù)似然比(LLR)消息,，v和u分別表示變量節(jié)點(diǎn)和校驗(yàn)節(jié)點(diǎn)發(fā)送給各自鄰接節(jié)點(diǎn)的LLR消息[2]。則變量節(jié)點(diǎn)和校驗(yàn)節(jié)點(diǎn)的消息更新規(guī)則表示為：
??? 
??? 在無(wú)環(huán)和不同變量節(jié)點(diǎn)初始消息u0服從獨(dú)立均勻分布(i.i.d.)的假設(shè)條件下,，易知,，ui,i=1,2,…,dv-1和vi,i=1,2,…,dc也是i.i.d.分布的。這樣計(jì)算ui和vi的概率密度函數(shù)變得容易,。在譯碼第k次迭代時(shí),，vi和ui的概率密度分別表示為Pk和Qk, k=1,2,…。P0表示u0的概率密度,，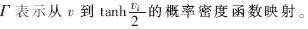
??? 基于上述的i.i.d.特性,，對(duì)于k≥1，從(1)式可得:
??? 
??? 
??? 在變量節(jié)點(diǎn)和校驗(yàn)節(jié)點(diǎn)進(jìn)行卷積運(yùn)算的域分別為i+(變量節(jié)點(diǎn)域:實(shí)數(shù)域加上+∞)和GF(2)×[0,∞](校驗(yàn)節(jié)點(diǎn)域:簡(jiǎn)稱(chēng)G域),利用傅立葉變換計(jì)算Qk和Pk時(shí),，在兩個(gè)域之間相互轉(zhuǎn)換,，從而使計(jì)算過(guò)程相當(dāng)復(fù)雜[4]。
2 密度進(jìn)化算法" title="進(jìn)化算法">進(jìn)化算法的實(shí)現(xiàn)
??? 密度進(jìn)化的實(shí)現(xiàn)主要包括三部分：變量節(jié)點(diǎn)域卷積,、G域卷積和兩個(gè)域之間適合卷積的密度函數(shù)表達(dá)式的相互轉(zhuǎn)換,。參考文獻(xiàn)[5-7]對(duì)不同的方法作了闡述，具有各自的特點(diǎn),。
2.1 離散密度進(jìn)化(DDE)
??? 為了計(jì)算機(jī)仿真處理,，對(duì)第1節(jié)算法中LLR消息、v,、u量化處理,。設(shè)量化比特為q,量化步進(jìn)為Δ，量化區(qū)間為[-N,N], N=2q-1-1,。如果消息值在范圍(nΔ-Δ/2,nΔ+Δ/2),，n是一個(gè)整數(shù)，當(dāng)-N≤n≤N時(shí)，消息量化為n,；當(dāng)n<-N和n>N時(shí),，分別量化為-N和N。
??? pv和pu分別表示離散消息的概率聚集函數(shù)(pmf),。由于離散消息都是獨(dú)立和均勻分布的隨機(jī)變量,，由(1)式易得變量節(jié)點(diǎn)的密度進(jìn)化規(guī)則為：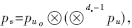
借助于快速傅立葉變換(FFT)能夠有效實(shí)現(xiàn)。
??? 對(duì)校驗(yàn)節(jié)點(diǎn)定義如下的二元運(yùn)算符Φ：
??? 
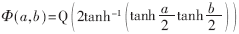
??? 其中a,、b都是離散消息,，Q表示量化運(yùn)算。易知Φ是遞歸運(yùn)算,，可以推導(dǎo)出校驗(yàn)節(jié)點(diǎn)密度進(jìn)化規(guī)則：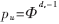
(pv),。采用查表法計(jì)算Φ，加速算法實(shí)現(xiàn),。
??? 對(duì)于非規(guī)則LDPC碼,，DDE算法是：
??? 
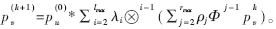
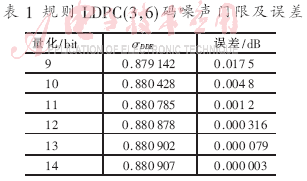
??? 該算法適合各種對(duì)稱(chēng)信道，如BSC,、BEC,、高斯信道等?？紤]AWGN信道,，LDPC(3,6)規(guī)則碼，信道噪聲方差σexact=0.880 91[3],，在不同量化比特情形下求得門(mén)限值σDDE如表1所示,，可見(jiàn)，量化14比特時(shí),，結(jié)果已相當(dāng)精確,。
?
?
2.2 利用對(duì)稱(chēng)傅立葉變換(SFT)計(jì)算
??? DDE算法在變量節(jié)點(diǎn)域未能充分利用LLR消息概率密度函數(shù)f的對(duì)稱(chēng)性。在對(duì)稱(chēng)信道上傳輸全1碼字時(shí),，f對(duì)稱(chēng),，從而g(x):=e-1/2x f(x)是偶函數(shù)。定義傅立葉變換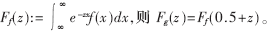
假設(shè)f取值于kδ,，k=-K,…,0,1,…,K,，對(duì)e-1/2 x f(x)填充0，進(jìn)行22m點(diǎn)離散傅立葉變換(2m+1>K),。實(shí)際中,，F(xiàn)g(jw)比Ff(jw)更有優(yōu)勢(shì)。首先,，前者是實(shí)數(shù)和關(guān)于w的偶函數(shù),，便于乘積計(jì)算,；其次，函數(shù)g的尾值呈指數(shù)級(jí)減少,，極大地降低了FFT計(jì)算時(shí)的混疊現(xiàn)象,。這樣，不必在每對(duì)卷積之后返回實(shí)數(shù)域,，只要在變量節(jié)點(diǎn)域卷積結(jié)束時(shí)返回即可,，節(jié)省了大量計(jì)算。
??? 在校驗(yàn)節(jié)點(diǎn)域,，即G域,，傅立葉變換定義為：Ff(v):=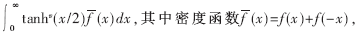
取值于實(shí)數(shù)[0,Kδ]U+∞。那么傅立葉變換：
??? 
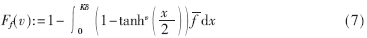
??? 現(xiàn)在的難題是如何量化v,。根據(jù)文獻(xiàn)[6],，實(shí)際采用v=eα(1+jw),。依照δ對(duì)α量化,，取w=0 將降低復(fù)雜度。
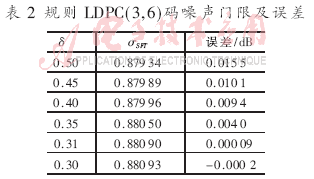
??? 這種算法比DDE更為接近原始的密度進(jìn)化原理,，但達(dá)到同樣精度需要少得多的計(jì)算量,。對(duì)于規(guī)則LDPC(3,6)碼，不同量化間隔時(shí)的噪聲門(mén)限σSFT如表2所示,。
?
?
2.3 高斯近似
??? 如果信道是AWGN,，消息的概率密度是近似高斯分布" title="高斯分布">高斯分布的。Wiberg[8]通過(guò)仿真首先發(fā)現(xiàn)這個(gè)事實(shí),。由于LLR消息的分布是相近的,，利用對(duì)數(shù)正態(tài)的性質(zhì)，可以證明在密度進(jìn)化過(guò)程中消息是近似高斯分布的,。利用對(duì)稱(chēng)條件f(x)=exf(-x),，高斯分布的LLR消息服從N(μ0,2μ0)。假設(shè)AWGN信道噪聲均值為0,，方差為σ2,，傳輸全0碼字，易知μ0=2/σ2,。只要確定?滋0就能完整描述概率密度函數(shù),。
??? mv和mu分別表示v和u的均值，則(1),、(2)式兩邊取均值,，化簡(jiǎn)變換可得：
??? 
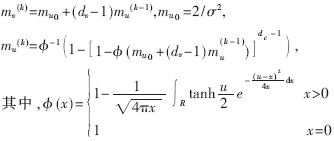
??? 其近似計(jì)算方法是：
??? 
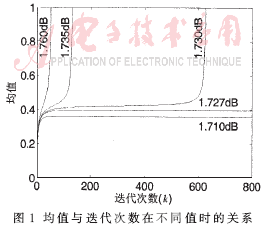
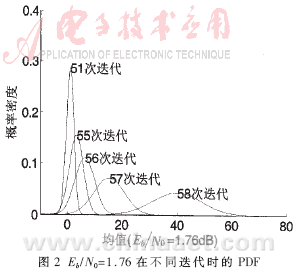
??? 用高斯近似算法求得規(guī)則LDPC(4,6)碼的噪聲門(mén)限為σGA=1.003 6，相應(yīng)的信噪比Eb/N0=1.729 9,。對(duì)于不同信噪比的消息概率密度的均值變化如圖1所示,。當(dāng)Eb/N0大于門(mén)限,，k→∞時(shí)，均值趨于無(wú)窮大,，意味著誤碼率趨于0,；當(dāng)Eb/N0小于門(mén)限，k→∞時(shí),，均值趨于一個(gè)有限固定值,，意味著誤碼率不可能趨于0。Eb/N0值越大,，正確譯碼需要的迭代次數(shù)越少,。當(dāng)Eb/N0=1.76時(shí)，概率密度分布如圖2所示,。隨著迭代次數(shù)的增長(zhǎng),，概率分布向正向移動(dòng)，譯碼器幾乎能夠正確譯碼,。
?
?
3 仿真和結(jié)論
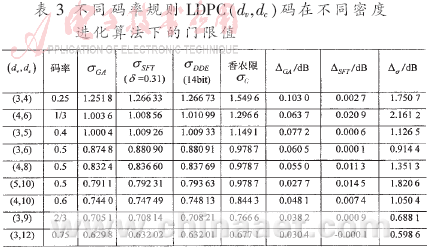
??? 前面討論的三種密度進(jìn)化算法各有特點(diǎn),。根據(jù)實(shí)際需要，選擇合適的算法對(duì)LDPC碼進(jìn)行研究,。表3給出了不同碼率的規(guī)則LDPC碼采用不同密度進(jìn)化算法求出的門(mén)限值,、σGA與σDDE的距離ΔGA、σSFT與σDDE的距離ΔSFT以及σDDE與香農(nóng)限σC的距離Δσ,。DDE和SFT兩種方法的精度差別不多,；高斯近似的精度稍微差些，但其計(jì)算量少很多,。
?
?
??? 表3中Δσ表明,，規(guī)則碼的門(mén)限值距離香農(nóng)限還較遠(yuǎn)。LDPC碼研究重點(diǎn)之一就是利用密度進(jìn)化算法優(yōu)化度分布(λ,ρ)設(shè)計(jì)好的非規(guī)則碼,，獲得距離香農(nóng)限更近的門(mén)限,。參考文獻(xiàn)[5]中設(shè)計(jì)出了Δσ=0.004 5dB的非規(guī)則碼，與香農(nóng)限的距離已經(jīng)很小了,。
??? 密度進(jìn)化方法是現(xiàn)代高級(jí)編碼研究的重要工具,不僅適用于LDPC碼,，也可用于Turbo碼、MN碼等的分析和設(shè)計(jì),。這種方法的提出,，促進(jìn)了現(xiàn)代高效糾錯(cuò)編碼的發(fā)展。
參考文獻(xiàn)
[1] GALLAGER R G. Low-Density Parity-Check codes.Cambridge, MA:MIT Press, 1963.
[2]?MACKAY D J C. Good? error-correcting codes based on very sparse matrices. IEEE Trans, Inf. Theory, 1999,45(3):399-431.
[3]?RICHARDSON T J, URBANKE R L. The capacity of? low-density? parity-check? codes? under message-passing decoding. IEEE? Trans. Information Theory, 2001,47(2):599-618.
[4]? RICHARDSON T, SHOKROLLAHI A,URABANKE R. Design of capacity- approaching irregular low-density parity-check codes. IEEE Trans. Inform. Theory, 2001,47(2):619-637.
[5]?CHUNG S Y, FORNEY G D, RICHARDSON J,et al. On the design of low-density parity -check codes within 0.0045 db of the Shannon limit. IEEE Communications Letters, 2001,5(2):58-60.
[6]?JIN H, RICHARDSON T. A new fast density evolution.IEEE Information Theory Workshop, Punta del Este, Uruguay, 2006:13-17.
[7]?CHUNG S Y, RICHARDSON T J, URBANKE R L. Analysis of sum-product decoding of low-density paritycheck codes using a Gaussian approximation. IEEE Trans. Inform. Theory,2001,47(2):657-670.
[8]?WIBERG N. Codes and decoding on general graphs. Ph.D. Dissertation,? Department? of Electrical Engineering, Linkoping?University, 1996.