摘 要: 多點(diǎn)組播是指一個(gè)源點(diǎn)傳送信息到多個(gè)目的節(jié)點(diǎn),它是網(wǎng)絡(luò)支持多媒體業(yè)務(wù)的關(guān)鍵技術(shù)之一。以服務(wù)質(zhì)量(QoS)指標(biāo)中的帶寬和時(shí)延為優(yōu)化選路準(zhǔn)則,提出了一種受限的組播路由算法,仿真結(jié)果證明了該算法的有效性。
關(guān)鍵詞: 網(wǎng)絡(luò) 組播 路由
通信網(wǎng)絡(luò)在進(jìn)入90年代后,向著綜合業(yè)務(wù)的方向發(fā)展。在傳統(tǒng)的數(shù)據(jù)網(wǎng)絡(luò)中,路由所需考慮的僅是可連接性[1],路由算法在尋找最優(yōu)(短)路徑時(shí)采用單一的指標(biāo),如跳數(shù)或時(shí)延。新出現(xiàn)的多媒體通信帶來了多點(diǎn)組播的需求,即未來的計(jì)算機(jī)網(wǎng)絡(luò)應(yīng)該能夠提供例如電視會(huì)議、視頻點(diǎn)播等具有點(diǎn)對(duì)多點(diǎn)的業(yè)務(wù)要求。而這種網(wǎng)絡(luò)應(yīng)該支持范圍廣泛的服務(wù)質(zhì)量(QoS)需求,確定路由需要相當(dāng)復(fù)雜的模型來描述網(wǎng)絡(luò),即路由的優(yōu)化指標(biāo)要包括時(shí)延、帶寬、丟失率等。
近年來,各國(guó)學(xué)者開始在這方面探索,提出了一些快速有效的算法。如:基于最短路徑的Dijkstra算法[2],即計(jì)算源點(diǎn)到各目的點(diǎn)的最短路徑;另一類是求最小網(wǎng)絡(luò)代價(jià)(NC)的應(yīng)用斯坦利(Steiner)樹路由算法[3],即計(jì)算組播樹(Multicast tree),使其在任意一對(duì)源和目的節(jié)點(diǎn)之間都存在通路,并使其代價(jià)(cost)最小。
本文使用改進(jìn)的受限Steiner樹路由算法,構(gòu)造樹型路由結(jié)構(gòu)來實(shí)現(xiàn)多點(diǎn)通信(multicast或MC)。這是由于基于樹實(shí)現(xiàn)有效MC路由具有以下兩個(gè)優(yōu)點(diǎn):(1)分組以并行方式沿著樹枝發(fā)送到不同的信宿;(2)網(wǎng)絡(luò)中需要傳送的復(fù)制分組最小,而且分組的復(fù)制只是在樹叉處進(jìn)行。在QoS的參數(shù)中,本文選取最小化占用鏈路總帶寬和滿足端到端的時(shí)延限制為優(yōu)化準(zhǔn)則。
1 受限組播路由的算法
1.1 網(wǎng)絡(luò)模型
一個(gè)網(wǎng)絡(luò)可以表示為圖G(V,E);其中V是頂點(diǎn)的集合,包括n個(gè)頂點(diǎn);E是邊的集合,包括m條邊。每條邊e∈E具有兩個(gè)參數(shù):C(e)和D(e),C(e)是邊e上的正實(shí)數(shù)代價(jià)函數(shù),D(e)是e上的正整數(shù)時(shí)延函數(shù)。在給定信源S和信宿集合D條件下,給定允許延遲極限Δ,構(gòu)造根為S,覆蓋所有信宿節(jié)點(diǎn)的受限Steiner樹,滿足條件![]() v∈D,樹上路徑(i,j)的延遲小于Δ,即:如果P(i、j)是樹上從i到j(luò)的路徑,那么對(duì)
v∈D,樹上路徑(i,j)的延遲小于Δ,即:如果P(i、j)是樹上從i到j(luò)的路徑,那么對(duì)![]() v∈D滿足:
v∈D滿足:
Σe∈PD(i、j)<Δ (1)
在滿足式(1)的條件下,
Σe∈PC(e)最小。 (2)
1.2 算法實(shí)現(xiàn)機(jī)理
由于網(wǎng)絡(luò)中的Steiner問題屬于圖論中的NP完備問題[4],即,一般地說,最優(yōu)算法無法在多項(xiàng)式時(shí)間內(nèi)完成。因此,用啟發(fā)式算法可降低算法難度,而在性能上逼近理論算法。由于構(gòu)造最小生成樹(MST)相對(duì)簡(jiǎn)單,因此常用的是MST啟發(fā)式算法。
本文通過改進(jìn)Prim算法[2]來求解MST問題。Prim算法的基本思想為:假定G=(V,E)是連通圖,T是G上MST中邊的集合。算法從U={S}(S為源點(diǎn)),T=Φ開始,重復(fù)執(zhí)行下列操作:在所有u∈U、v∈{V-U}的邊(u、v)∈E中找一條權(quán)值最小的邊(u0、v0)并入集合T,同時(shí)u0并入U(xiǎn),直到U=V為止,則T為G的MST。
改進(jìn)算法的基本思想是:首先利用Dijkstra第k最短路徑算法,計(jì)算從源節(jié)點(diǎn)到目的節(jié)點(diǎn)以時(shí)延為優(yōu)化準(zhǔn)則的路徑,并將所求的路徑中最大的時(shí)延與Δ比較,若該值比Δ大則表明限制條件太苛刻,可令Δ等于該值。然后以cost最小為首要優(yōu)化目標(biāo),用Prim算法求出圖G的MST樹。用Prim算法每生成一條邊(i、j)時(shí),就計(jì)算由S到該邊的累計(jì)時(shí)延Σe∈PD(i、j)、若Σe∈PD(i、j)≤Δ,則用Prim算法繼續(xù)尋找下一條邊。否則令該邊對(duì)應(yīng)的cost(i、j)為∞,并且將j(i∈U、j∈{V-U})仍保留在原來集合中。當(dāng)用Prim算法完成一次全局搜索后,再對(duì)那些仍保留在{V-U}集合中的點(diǎn)重新進(jìn)行全局搜索(除開前次讓cost(i、j)為∞的i點(diǎn)外),尋找符合時(shí)延條件的新邊。當(dāng)U中已包含全部組播目標(biāo)節(jié)點(diǎn)Di后,算法結(jié)束。
1.3 算法的實(shí)現(xiàn)過程
可采用一個(gè)整型二維數(shù)組a[MAX][3]來表示在構(gòu)造最小生成樹U,{V-U}和權(quán)值cost的變化。其中數(shù)組的第一列a[][0]放生成樹的頂點(diǎn)集合U中的各頂點(diǎn),初始值為源點(diǎn)s;第二列a[][1]放頂點(diǎn)集合{V-U}中的各頂點(diǎn);第三列a[][2]放{V-U}到U所構(gòu)成的邊的最小權(quán)值。同時(shí),采用二維數(shù)組mat[MAX][MAX]來存儲(chǔ)圖的鄰接矩陣,矩陣(i、j)對(duì)應(yīng)的值就是邊(i、j)上的cost值。開始對(duì)a[MAX][3]的初始化可表示為:
a[i][0]=1;
if(i==1)
a[i][1]=0;
else
a[i][1]=i;
a[i][2]=mat[1][i];
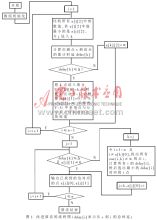
然后按前面所述的改進(jìn)Prim算法來搜索MST。具體實(shí)現(xiàn)過程可以用C語(yǔ)言編程實(shí)現(xiàn)。其流程圖如圖1所示。這里設(shè)Δ是合理的時(shí)延限制值,且整個(gè)網(wǎng)絡(luò)有n個(gè)節(jié)點(diǎn)。
2 仿真及實(shí)驗(yàn)結(jié)果
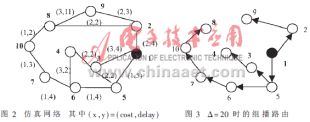
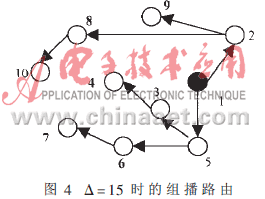
采用文章中提出的算法在圖2所示結(jié)構(gòu)的網(wǎng)絡(luò)(設(shè)為無向圖)上進(jìn)行仿真(其中節(jié)點(diǎn)1為源點(diǎn)S,節(jié)點(diǎn)4、5、6、7、8、9、10為目的節(jié)點(diǎn))設(shè)Δ=20和15時(shí)均能得到建立在受限Steiner最小樹上的組播路由。結(jié)果如圖3和圖4所示。
?
本文提出的算法兼顧了滿足時(shí)延限制和代價(jià)最小兩個(gè)QoS要求,仿真結(jié)果也證明了該算法在力求代介最小的前提下,能根據(jù)組播應(yīng)用時(shí)延的限制要求,快速有效地構(gòu)造組播樹,有較強(qiáng)的實(shí)時(shí)性。
參考文獻(xiàn)
1 Gupta S. On routing in ATM networks、modeling and performance evaluation of ATM Technology.North-Holland:Elsevier Science Publisher B.V、1993:229~239
2 劉振宏,蔡茂誠(chéng)譯.組合最優(yōu)化.北京:清華大學(xué)出版社,1998
3 Hwang F K、Richards D S.Steiner tree problems.IEEE Networks、1992;22(1):55~89
4 M.R.Garey and D.S.Johnson、Computers and Intractability:A Guide to the Theory of NP-Completeness. San Francisco、CA:Freeman、1979