圖像融合的主要目的是綜合各類(lèi)圖像數(shù)據(jù)的優(yōu)點(diǎn),提高圖像的解譯能力[1]。圖像融合技術(shù)已廣泛應(yīng)用于軍事,、遙感,、計(jì)算機(jī)視覺(jué)和醫(yī)學(xué)等領(lǐng)域,。目前比較典型的圖像融合方法有:基于小波圖像的融合方法兩種[2-3]和基于數(shù)學(xué)形態(tài)學(xué)[4]的融合方法。這兩種方法簡(jiǎn)單,，容易實(shí)時(shí)處理,，但是融合的精度不高,忽略了子圖像中邊緣信息細(xì)節(jié)丟失問(wèn)題,從而影響了融合圖像的清晰度和信息熵。
    多小波變換圖像融合方法是在小波理論基礎(chǔ)上發(fā)展起來(lái)的,，多小波是指由兩個(gè)或者兩個(gè)以上的函數(shù)作為尺度函數(shù)生成的小波,。夏明革[5]等人提出了在多小波變換域?qū)Φ皖l系數(shù)和高頻系數(shù)分別采用取絕對(duì)值最大和絕對(duì)值最小的融合規(guī)則。劉峰[6]等人提出了在多小波變換域?qū)Φ皖l系數(shù)和高頻系數(shù)分別采用基于區(qū)域均方誤差加權(quán)平均的方法和區(qū)域能量匹配的方法,。融合結(jié)果得到了改善,，可是沒(méi)有能夠較好地保留原圖像的細(xì)節(jié)和邊緣。
    針對(duì)這一問(wèn)題,，本文給出了一種形態(tài)學(xué)多小波變換多聚焦圖像融合方法,。該方法利用不同的小波對(duì)待融合圖像進(jìn)行小波分解，利用一種新的抗噪型的形態(tài)學(xué)灰度形態(tài)梯度邊緣檢測(cè)算子來(lái)檢測(cè)低頻子圖像邊緣信息,，以確保邊緣信息的完整,；對(duì)高頻系數(shù)選擇采用基于加權(quán)平均方法。本方法有效地防止了邊緣信息丟失,提高了圖像融合的質(zhì)量,。
1 數(shù)學(xué)形態(tài)學(xué)
    數(shù)學(xué)形態(tài)學(xué)[7-8]是一門(mén)建立在嚴(yán)格數(shù)學(xué)理論基礎(chǔ)上的學(xué)科,，其基本思想是用具有一定形態(tài)的結(jié)構(gòu)元素去度量和提取圖像中的對(duì)應(yīng)形狀以達(dá)到對(duì)圖像分析和識(shí)別的目的。數(shù)學(xué)形態(tài)學(xué)的應(yīng)用可以簡(jiǎn)化圖像數(shù)據(jù),，保持它們基本的形狀特征,，并除去不相干的結(jié)構(gòu)。數(shù)學(xué)形態(tài)學(xué)的基本運(yùn)算有膨脹,、腐蝕,、開(kāi)啟和閉合(具體運(yùn)算不作闡述)。
    灰度膨脹邊緣檢測(cè)算子：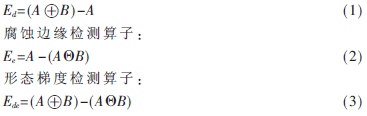

    由于灰度膨脹邊緣檢測(cè)算子主要是基于形態(tài)膨脹,，得到的邊緣信號(hào)較弱,所產(chǎn)生圖像的邊緣比較模糊,。腐蝕邊緣檢測(cè)算子主要是基于形態(tài)腐蝕，它所得到的圖像邊緣信號(hào)較強(qiáng),，但是會(huì)增加圖像的噪聲。所以本文對(duì)傳統(tǒng)的檢測(cè)算子做了改進(jìn),，采用結(jié)合形態(tài)學(xué)開(kāi)啟與閉合運(yùn)算,，提出了一種新的抗噪型灰度形態(tài)梯度邊緣檢測(cè)算子，其算子公式如下：

2 單一小波變換
    Mallat 提出了小波變換的快速分解算法與重構(gòu)算法, 即利用兩個(gè)一維濾波器實(shí)現(xiàn)對(duì)二維圖像的快速分解, 再利用兩個(gè)二維濾波器實(shí)現(xiàn)圖像的重構(gòu),。其對(duì)應(yīng)的濾波器系數(shù)矩陣分別為H和G,，則Mallat算法在j尺度下的分解公式[9]為：
 
3 多小波變換
    多小波變換是在單一小波理論基礎(chǔ)上發(fā)展而來(lái)的，是建立在多分辨率分析基礎(chǔ)上的,與單小波變換類(lèi)似,，如果生成多小波Ψ(x)相對(duì)應(yīng)的多尺度函數(shù)Φ=(Φ1,Φ2,…,Φr)T滿足r階的多分辨分析MRA{Vj},，則稱(chēng)Φ是MRA^T的多尺度函數(shù),。如果Φ是正交的,則稱(chēng){Vj}是正交的MRA^T。
    由多分辨率分析的定義可知,，存在r×r矩陣Hk,、Gk(r=2)，使得滿足下列兩個(gè)尺度方程[10]:

4 基于形態(tài)學(xué)多小波變換圖像融合算法
    假設(shè)兩幅待融合圖像F和E,，經(jīng)過(guò)小波N層分解,，分解得到不同的頻率域，在不同的頻率域選用不同的融合規(guī)則得到合成圖像的多分辨率分解, 然后重構(gòu)得到融合圖像,。多小波變換圖像融合流程圖如圖1所示,。

    下面分別對(duì)低頻域和高頻域給出各自的融合算法。高頻系數(shù)反映了圖像的細(xì)節(jié),，其選擇規(guī)則決定了融合圖像對(duì)原圖像細(xì)節(jié)的保留程度,。本文在選擇高頻系數(shù)時(shí)，采用基于加權(quán)平均的方法,，對(duì)兩幅圖像多小波分解后高頻系數(shù)取平均值：

式中,，Dj為融合后圖像在第j級(jí)的高頻系數(shù),DjF為圖像F在第j級(jí)高頻系數(shù)，DjE為圖像E在第j級(jí)高頻系數(shù),。
    對(duì)于低頻系數(shù),，采用一種新的抗噪型灰度形態(tài)梯度邊緣檢測(cè)算子對(duì)低頻子圖像進(jìn)行邊緣檢測(cè)。由于形態(tài)梯度邊緣檢測(cè)需要確定梯度的方向以及模值,，同時(shí)由于小波模值和形態(tài)梯度值的關(guān)系[12],，所以設(shè)定一個(gè)門(mén)限的模極大值ε，只需要沿著各個(gè)小波變換的方向來(lái)尋找大于門(mén)限的模極大值?著即可,。
    對(duì)于圖像F定義如下：

式中,，VF、VE包含了水平方向,、垂直方向以及對(duì)角線方向上的邊緣信息,，因此本方法的角度μ取垂直、水平和對(duì)角線4個(gè)方向,，沿著這4個(gè)方向搜尋多小波變換模極大值,，就能夠找到在該方向上的邊緣信息。對(duì)于VF和VE,，選擇其中值較大的一個(gè)所對(duì)應(yīng)的系數(shù)作為融合圖像的低頻系數(shù),，就能最大程度地在融合圖像中保留原圖像的邊緣細(xì)節(jié)。
5 仿真實(shí)驗(yàn)與結(jié)果分析
    為了說(shuō)明本文算法的有效性,，在MATLAB7.0實(shí)驗(yàn)環(huán)境下,采用聚焦點(diǎn)不同的兩幅圖像做了實(shí)驗(yàn),。根據(jù)本文所提出的方法，對(duì)Floclo圖像和Veg圖像進(jìn)行了仿真實(shí)驗(yàn)，并且與傳統(tǒng)的圖像融合方法進(jìn)行了比較,。其結(jié)果如圖2,、圖3所示。

     從主觀效果來(lái)看,，本算法能夠較好地保留細(xì)節(jié)部分,，相對(duì)比其他幾種傳統(tǒng)的圖像融合方法，本方法有明顯的優(yōu)勢(shì),。為了更好地給出Floclo和Veg圖像融合算法的性能評(píng)價(jià),，引入熵值[13]來(lái)進(jìn)行評(píng)價(jià)，如表1所示,。

    圖像的熵值的大小反映了圖像所包含的平均信息量的多少,，圖像的熵定義：

式中，H為圖像的熵,，N為圖像灰度級(jí),，pi為像素級(jí)為i的出現(xiàn)的相對(duì)頻率。
    本文主要針對(duì)圖像融合中邊緣信息容易丟失等問(wèn)題,，提出了一種形態(tài)學(xué)多小波變換多聚焦圖像融合方法,。該方法采用一種新的抗噪型形態(tài)學(xué)灰度形態(tài)梯度檢測(cè)算子檢測(cè)小波分解后低頻子圖像邊緣信息，采用加權(quán)平均法選擇高頻系數(shù),。將這一算法應(yīng)用于兩組多聚焦圖像中,，并與幾種傳統(tǒng)的圖像融合方法進(jìn)行了比較，對(duì)實(shí)驗(yàn)結(jié)果的分析得出,，基于形態(tài)學(xué)多小波變換多聚焦圖像融合方法的融合效果明顯,。
參考文獻(xiàn)
[1] PIELLA G. A general framework formultiresolution image  fusion：from Pixels to regions[J].Information Fusion,2003,68(4):259-280.
[2] BURT P J，KOLCZYNSKI R J. Enhanced image capture through fusion[C]． Proceedings International Conference on  Computer Vision．1993.
[3] DE I,CHANDA B, CHATTOPADHYAY B. Enhancing effective depth-of-field by image fusion using mathematical  morphology[J]. Image and Vision Computing, 2006,24(12):1278-1287.
[4] Tao G Q,， Li D P,， Lu G H． On image fusion based on different fusion rules of wavelet transform[J]．Acta Photonica  Sinica，2004,，33(2)：222.
[5] 夏明革,，何友，蘇峰. 基于多小波分析的圖像融合算法[J]. 電光與控制,，2005,12（2）：19-22.
[6] 劉峰,，姬光榮，周立儉. 基于多小波分析圖像融合算法[J]. 中國(guó)海洋大學(xué)學(xué)報(bào),，2007,37（1）：163-167.
[7] 唐常青.數(shù)學(xué)形態(tài)學(xué)方法及其應(yīng)用[M].北京:科學(xué)技術(shù)出版社,1990.
[8] 戴青云,余英林.數(shù)學(xué)形態(tài)學(xué)在圖像處理中的應(yīng)用進(jìn)展[J].控制理論與應(yīng)用,2001,18(4):478-482.
[9] 楊福生.小波變換的工程與應(yīng)用[M].北京:科學(xué)出版社,2000.
[10] 那彥,，史林，楊萬(wàn)海.基于成像機(jī)理的多小波多聚焦圖像融合[J]. 系統(tǒng)工程與電子技術(shù),，2004,26(11):1549-1551.
[11] 朱四榮，王迎春. 基于多小波變換的多聚焦圖像融合[J]. 計(jì)算機(jī)工程與應(yīng)用,，2010,46(6)：169-171.
[12] 晁銳,，張科,，李言俊. 一種基于小波變換的圖像融合算法[J]. 電子學(xué)報(bào)，2004,，32(5):750-753.
[13] 燕文浩,，馬彩文，張鳴,，等. 基于小波變換的圖像融合新算法[J].光子學(xué)報(bào),，2006，35(4):638-640.