摘  要： 為了有效提高混凝土抗壓強度的預(yù)測精準(zhǔn)度,，利用粒子群算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)初始權(quán)值和閾值,，建立了混凝土抗壓強多因子PSO-BP預(yù)測模型。模型以每立方混凝土中水泥,、高爐礦渣粉,、粉煤灰、水,、減水劑,、粗集料和細集料的含量以及置放天數(shù)為輸入?yún)?shù)，混凝土抗壓強度值作為輸出參數(shù),，不僅可以克服BP算法收斂速度慢和易陷入局部極值的缺陷，而且模型的學(xué)習(xí)能力,、泛化能力和預(yù)測精度都有了很大的提高,。以UCI數(shù)據(jù)庫中的Concrete Compressive Strength數(shù)據(jù)集為例進行仿真測試，結(jié)果表明：PSO-BP模型預(yù)測精度較BP,、GA-BP模型分別提高了8.26%和2.05%,，驗證了PSO-BP模型在混凝土抗壓強度預(yù)測中的有效性。
關(guān)鍵詞： BP神經(jīng)網(wǎng)絡(luò),；粒子群算法,；混凝土抗壓強度,；預(yù)測

    混凝土抗壓強度是否符合預(yù)期規(guī)定是其質(zhì)量控制的重要研究內(nèi)容之一，準(zhǔn)確預(yù)測混凝土抗壓強度對施工質(zhì)量的提高,、工程進度的加快有著重要作用[1],。對于普通混凝土的強度，一般可以用灰水比為主要因素的線性函數(shù)來進行描述和預(yù)測,。對于高摻量的粉煤灰和礦渣混凝土來說,，由于其組分的增加，水化反應(yīng)的機理還不完全明確,，影響因素更為復(fù)雜并具有交互作用,，表現(xiàn)為特定的非線性規(guī)律[2]。人工神經(jīng)網(wǎng)絡(luò)(ANN)是解決非線性問題的有效手段之一,，其中BP網(wǎng)絡(luò)由于結(jié)構(gòu)簡單,、易于實現(xiàn)、魯棒性強等特點,，成為神經(jīng)網(wǎng)絡(luò)中運用較多的網(wǎng)絡(luò)之一,。但是BP神經(jīng)網(wǎng)絡(luò)也具有一些固有的弱點，如算法容易陷入局部極小點,、收斂速度慢等,，限制了它的進一步應(yīng)用。
    粒子群優(yōu)化算法(PSO)避免了梯度下降法中要求函數(shù)可微,、對函數(shù)求導(dǎo)的過程,，采用基于種群全局搜索策略，而且其采用的速度—搜索模型操作簡單,。它特有的記憶使其可以動態(tài)跟蹤當(dāng)前的搜索情況,，調(diào)整其搜索策略，可大大縮短神經(jīng)網(wǎng)絡(luò)的訓(xùn)練時間[3],?；诖耍疚牟捎昧Ｗ尤核惴▋?yōu)化BP神經(jīng)網(wǎng)絡(luò)的權(quán)值和閾值,，并利用訓(xùn)練樣本建立了混凝土抗壓強度PSO-BP預(yù)測模型,。然后利用此模型對測試樣本進行預(yù)測，得到測試樣本抗壓強度值和誤差,，并將結(jié)果與BP,、GA-BP網(wǎng)絡(luò)進行比較，來驗證該模型在混凝土抗壓強度預(yù)測中的可靠性和適用性,。
1 PSO-BP模型的建立
1.1 BP神經(jīng)網(wǎng)絡(luò)基本原理
    BP(Back Propagation)神經(jīng)網(wǎng)絡(luò)是一種神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)算法,，全稱為基于誤差反向傳播算法的人工神經(jīng)網(wǎng)絡(luò)，由信息的正向傳播和誤差的反向傳播兩個過程組成。輸入層各神經(jīng)元負(fù)責(zé)接收來自外界的輸入信息,， 并傳遞給中間層各神經(jīng)元,；中間層是內(nèi)部信息處理層，負(fù)責(zé)信息交換,。根據(jù)信息變化能力的需求,，中間層可以設(shè)計為單隱層或多隱層結(jié)構(gòu)； 最后一個隱層傳遞到輸出層各神經(jīng)元的信息,，經(jīng)進一步處理后,， 完成一次學(xué)習(xí)的正向傳播，由輸出層向外界輸出信息處理結(jié)果,。當(dāng)實際輸出與期望輸出不符時,，進入誤差的反向傳播階段。隱含層中神經(jīng)元的轉(zhuǎn)換函數(shù)有多種,，通常采用log-sigmoid型函數(shù),。層與層之間采用全互聯(lián)的方式，以三層網(wǎng)絡(luò)為例,，其BP網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu)如圖1所示[4],。一個具有3層的BP神經(jīng)網(wǎng)絡(luò)能夠以任意精度逼近任意連續(xù)函數(shù)，具有很強的非線性映射能力以及自學(xué)習(xí),、自組織和自適應(yīng)能力,，因此本文選用三層BP神經(jīng)網(wǎng)絡(luò)。

  

   
2.3 實驗結(jié)果與分析
    對于1 030組實驗數(shù)據(jù),，本文隨機選取1 020組作為訓(xùn)練數(shù)據(jù),，用剩余10組作為測試數(shù)據(jù)。利用Matlab神經(jīng)網(wǎng)絡(luò)工具箱和PSO工具箱編制PSO-BP混凝土抗壓強度預(yù)測程序,，將PSO中粒子的位置映射為BP神經(jīng)網(wǎng)絡(luò)的初始權(quán)值和閾值,，通過BP算法訓(xùn)練網(wǎng)絡(luò)，直到網(wǎng)絡(luò)達到性能指標(biāo),。圖2給出了PSO優(yōu)化過程中最優(yōu)個體適應(yīng)度變化曲線,，可見適應(yīng)度值從最初的6.5經(jīng)過20代左右快速收斂到了4.5。

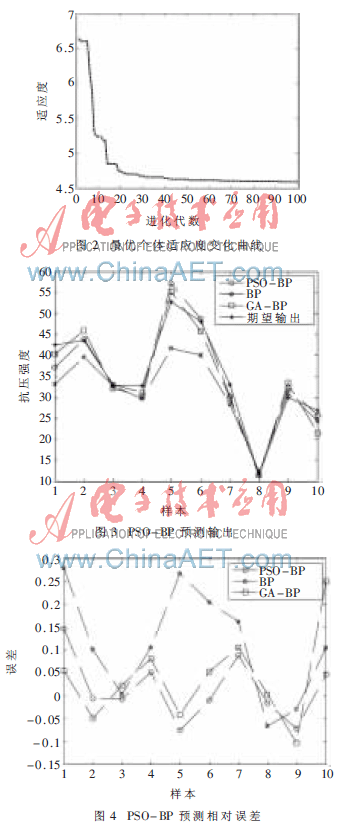
    用訓(xùn)練好的PSO-BP模型對測試樣本進行測試,，得到測試樣本的預(yù)測結(jié)果,。圖3給出了10個測試樣本的預(yù)測輸出，從圖中可以看出,，PSO-BP模型的吻合度要比BP,、GA-BP高許多。圖4給出了預(yù)測相對誤差,，可以更進一步看出，除了個別樣本,，PSO-BP模型預(yù)測誤差曲線在零附近的震蕩和偏差都要小于BP,、GA-BP模型,。表1列出了PSO-BP、BP和GA-BP模型分別對10組測試樣本的預(yù)測輸出和相對誤差,。

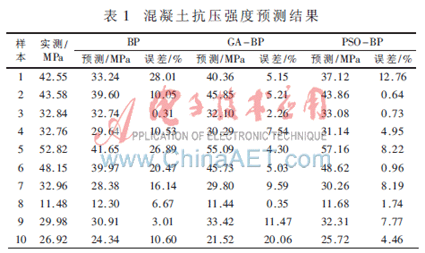
    觀察表1,，對于10組測試樣本，預(yù)測相對誤差小于15%的,，PSO-BP,、BP和GA-BP分別為10例、6例和9例,，相對誤差平均值分別為5.04%,、13.30%和7.09%；PSO-BP模型預(yù)測精度較BP,、GA-BP模型分別提高了8.26%和2.05%,。可見,，PSO-BP模型的預(yù)測準(zhǔn)確度要優(yōu)于BP,、GA-BP，這為混凝土的抗壓強度提供了一個更精準(zhǔn)的預(yù)測方法,。
    傳統(tǒng)的混凝土抗壓強度線性預(yù)測方法存在諸多不足,，采用人工智能技術(shù)較好地解決了這個問題。將粒子群算法與BP神經(jīng)網(wǎng)絡(luò)相結(jié)合,，建立的PSO-BP模型兼有人工神經(jīng)網(wǎng)絡(luò)的廣泛映射能力和粒子群算法的全局收斂以及啟發(fā)式學(xué)習(xí)等優(yōu)點,，明顯提高了網(wǎng)絡(luò)的泛化能力和運算效率。將PSO-BP模型運用于混凝土抗壓強度預(yù)測研究中,，結(jié)果表明該模型具有較高的預(yù)測精度,，可以在混凝土工程中進行實際運用。
參考文獻
[1] 季韜,，林挺偉,，林旭健.基于人工神經(jīng)網(wǎng)絡(luò)的混凝土抗壓強度預(yù)測方法[J].建筑材料學(xué)報,2005，8(6)：676-681.
[2] 廖小輝,，黃新,，施俊玲，等.基于BP網(wǎng)絡(luò)的再生混凝土抗壓強度的預(yù)測模型[J].南京林業(yè)大學(xué)學(xué)報(自然科學(xué)版),，2010,，34(5)：105-108.
[3] 任洪娥，霍滿冬.基于PSO優(yōu)化的SVM預(yù)測應(yīng)用研究[J].計算機應(yīng)用研究,，2009,，26(3)：867-869.
[4] 張鵬，趙鐵軍，李秋義,，等.雙摻粉煤灰和礦渣混凝土強度的BP網(wǎng)絡(luò)預(yù)測模型[J].混凝土,，2009(6)：16-18.
[5] 婁偉平，陳海燕,，邱新法,，等.基于粒子群優(yōu)化神經(jīng)網(wǎng)絡(luò)的臺風(fēng)災(zāi)情定量評估[J].自然災(zāi)害學(xué)報, 2010，19(4)：136-139.
[6] YI D,，GE X R.An improved PSO based ANN with simulated annealing technique[J].Neurocomputing,，2005，63(11)：527-533.
[7] MATLAB中文論壇編著.MATLAB神經(jīng)網(wǎng)絡(luò)30個案例分析[M].北京：北京航空航天大學(xué)出版社,，2010.
[8] YEH I C.Modeling of strength of high performance concrete using artificial neural networks[J],Cement and Concrete Research,，1998，12(28)：1797-1808.