《電子技術(shù)應(yīng)用》
您所在的位置：首頁(yè) > EDA與制造 > 設(shè)計(jì)應(yīng)用 > 改進(jìn)溢出判斷電路的設(shè)計(jì)與仿真研究
改進(jìn)溢出判斷電路的設(shè)計(jì)與仿真研究
來源：電子技術(shù)應(yīng)用2012年第5期
王 穎1,，王瑞春2
1.深圳信息職業(yè)技術(shù)學(xué)院 電子與信息學(xué)院,，廣東 深圳518055； 2.深圳信息職業(yè)技術(shù)學(xué)院 基礎(chǔ)部,，廣東 深圳518055
摘要： 傳統(tǒng)數(shù)字芯片電路中,，固定字長(zhǎng)有符號(hào)數(shù)的加法或減法運(yùn)算的溢出判斷需要等到加法/減法運(yùn)算結(jié)束之后才能進(jìn)行。以四位有符號(hào)數(shù)加法/減法運(yùn)算溢出判斷邏輯為例提出一種改進(jìn)的設(shè)計(jì)方式,，能夠在加法/減法運(yùn)算結(jié)束之前對(duì)操作數(shù)進(jìn)行判斷,，從而決定是否有溢出現(xiàn)象的發(fā)生。仿真發(fā)現(xiàn),，改進(jìn)后的電路無論在規(guī)模上還是在運(yùn)算速度上都有很大改善,。
中圖分類號(hào)： TP302.1
文獻(xiàn)標(biāo)識(shí)碼： A
文章編號(hào)： 0258-7998(2012)05-0049-03
Research on design and simulation of an improved overflow judgment circuit
Wang Ying1，Wang Ruichun2
1.School of Electronic and Telecom Technology ,Shenzhen Institute of Information Technology,Shenzhen 518055,，China,； 2.Department of Basic Research, Shenzhen Institute of Information Technology,Shenzhen 518055，China
Abstract： In the typical overflow judgment circuit , the existence of overflow can not be judged until the operation is end. In this paper, an improved design is put forward. The improved design is based on the addition or subtraction of four-bit signed data. This improved circuit can judge the existence of overflow by view the operator before the end of the operation. The improved circuit is found better in the scale and delay time by simulation.
Key words : improvement,；over-flow judgment,；circuit design；simulation

    溢出現(xiàn)象的判斷是固定字長(zhǎng)有符號(hào)加法運(yùn)算中必須要進(jìn)行的操作,，傳統(tǒng)溢出現(xiàn)象的判斷要等到加法運(yùn)算結(jié)果產(chǎn)生以后才能進(jìn)行,，本文電路設(shè)計(jì)能夠在加法運(yùn)算開始之前通過對(duì)操作數(shù)的判斷而進(jìn)行溢出預(yù)判，從而減少了整個(gè)加法/減法運(yùn)算的時(shí)間,。

    溢出現(xiàn)象有可能出現(xiàn)在有符號(hào)數(shù)的加法或減法運(yùn)算中,，在進(jìn)行固定字長(zhǎng)的有符號(hào)數(shù)加法或減法運(yùn)算時(shí)，如果出現(xiàn)以下四種情況：正數(shù)與正數(shù)相加得到負(fù)數(shù),、正數(shù)減負(fù)數(shù)得到負(fù)數(shù),、負(fù)數(shù)減正數(shù)得到正數(shù)、負(fù)數(shù)加負(fù)數(shù)得到正數(shù),，則認(rèn)為有溢出現(xiàn)象產(chǎn)生,。
1 傳統(tǒng)溢出判斷電路的設(shè)計(jì)[1]
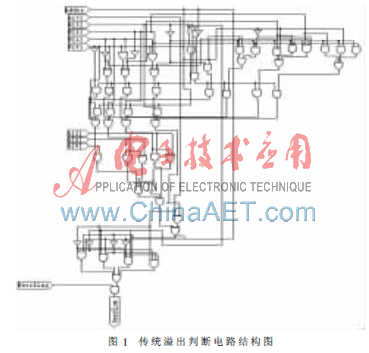
    傳統(tǒng)溢出判斷電路的設(shè)計(jì)是建立在加法或減法運(yùn)算已經(jīng)產(chǎn)生結(jié)果的基礎(chǔ)上，如果用Overflag表示當(dāng)前的運(yùn)算方式,，當(dāng)Overflag取值為“1”時(shí)表示的是進(jìn)行有符號(hào)數(shù)的加法或減法運(yùn)算,，當(dāng)Overflag取值為“0”時(shí)表示的是進(jìn)行無符號(hào)數(shù)的加法或減法運(yùn)算,。用Adder表示當(dāng)前的運(yùn)算方式是加法或者減法運(yùn)算。當(dāng)Adder取值為“1”時(shí)表示進(jìn)行加法運(yùn)算,，當(dāng)Adder取值為“0”時(shí)表示進(jìn)行減法運(yùn)算,。用A[3]、B[3]和R[3]分別表示兩個(gè)操作數(shù)和加減法運(yùn)算結(jié)果的最高位即符號(hào)位,。用Overflow表示溢出結(jié)果,，如果Overflow取值為“1”則表示產(chǎn)生了溢出；如果Overflow取值為“0”則表示沒有產(chǎn)生溢出,。如果利用Carry-Lookahead Adder[2]算法來產(chǎn)生R[3],，則結(jié)合對(duì)溢出產(chǎn)生條件的分析，可以得到溢出判斷電路圖如圖1所示,。

2 具有預(yù)判功能的改進(jìn)溢出判斷電路的設(shè)計(jì)
    具有預(yù)判功能的溢出判斷電路設(shè)計(jì)的原理是將Carry-Lookahead Adder[2]的算法與傳統(tǒng)溢出邏輯判斷邏輯算法相結(jié)合,。如果將可能產(chǎn)生溢出的四種運(yùn)算都轉(zhuǎn)換為加法運(yùn)算，則在有可能產(chǎn)生溢出的四種運(yùn)算情況下只要數(shù)值位向符號(hào)位產(chǎn)生進(jìn)位或者符號(hào)位本身相加產(chǎn)生進(jìn)位就可以判斷有溢出產(chǎn)生,。因此在電路實(shí)現(xiàn)上需要有兩部分功能塊,，一部分是判斷當(dāng)前的運(yùn)算是否為可能產(chǎn)生溢出的四種運(yùn)算，將這部分功能塊稱為初步判斷功能塊,；另一部分是判斷數(shù)值位的最高位有無向符號(hào)位產(chǎn)生進(jìn)位或符號(hào)位本身相加有無進(jìn)位產(chǎn)生,，將這部分功能塊稱為進(jìn)位判斷功能塊。最后需要將兩部分功能塊結(jié)合在一起成為完整的溢出預(yù)判電路,。

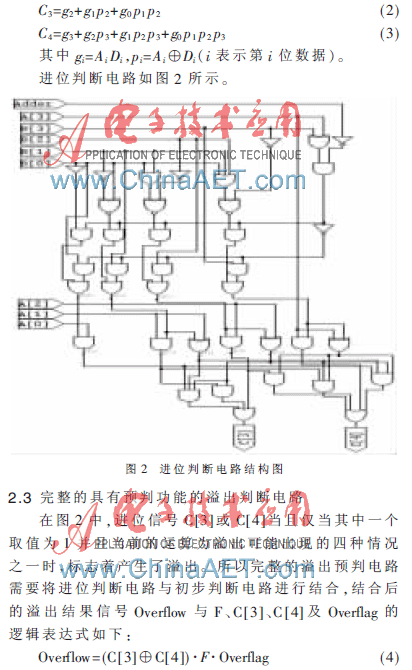
2.2 進(jìn)位判斷功能塊[2]
    在對(duì)溢出現(xiàn)象進(jìn)行分析的過程中發(fā)現(xiàn),，可能產(chǎn)生溢出的四種情況的運(yùn)算最后都可以轉(zhuǎn)換為加法運(yùn)算，具體分析如下：
    正數(shù)與正數(shù)相加,，原本就是加法運(yùn)算,，所以毋須進(jìn)行轉(zhuǎn)換。
    正數(shù)減負(fù)數(shù)相當(dāng)于正數(shù)與同負(fù)數(shù)有相同絕對(duì)取值的正數(shù)進(jìn)行相加,。即只要將被減數(shù)轉(zhuǎn)換成與其本身有相同絕對(duì)取值的正數(shù)即可,。
    負(fù)數(shù)減正數(shù)相當(dāng)于負(fù)數(shù)與同正數(shù)有相同絕對(duì)取值的負(fù)數(shù)進(jìn)行相加。即只要將被減數(shù)轉(zhuǎn)換成與其本身有相同絕對(duì)取值的負(fù)數(shù)即可,。
    負(fù)數(shù)加負(fù)數(shù)本身就是加法運(yùn)算,，毋須進(jìn)行轉(zhuǎn)換。
    假設(shè)A為加法或減法運(yùn)算中的第一個(gè)操作數(shù)（被加數(shù)或被減數(shù)）,，B為第二個(gè)操作數(shù)（加數(shù)或減數(shù)），由以上分析可以發(fā)現(xiàn),，A不需要做任何變換,，而B要根據(jù)需要進(jìn)行變換，變換后的數(shù)字用D進(jìn)行表示,。對(duì)B進(jìn)行變換的算法為：首先判斷條件“A[3]=0且B[3]=1且Adder=0”或“A[3]=1且B[3]=0且Adder=0”是否成立,，如果條件成立,，則D的值等于對(duì)B做減1運(yùn)算后再取反的數(shù)值，否則D=B,。
    操作數(shù)B做了變換后,，A與B的運(yùn)算就轉(zhuǎn)換成A與D的加法運(yùn)算，運(yùn)算結(jié)果用R表示,。通過前面的分析可以發(fā)現(xiàn)在可能產(chǎn)生溢出的四種運(yùn)算情況下（即：正數(shù)與正數(shù)相加,、負(fù)數(shù)與負(fù)數(shù)相加、正數(shù)與負(fù)數(shù)相減,、負(fù)數(shù)與正數(shù)相減）,，只要A與D的加法運(yùn)算的結(jié)果中符號(hào)位的符號(hào)與操作數(shù)符號(hào)相反就標(biāo)志著產(chǎn)生了溢出。用Ci+1表示第i位向第i+1位產(chǎn)生的進(jìn)位,，則C3=1或C4=1且C3 和C4不能同時(shí)為1時(shí)標(biāo)志著溢出的產(chǎn)生,。
    通過對(duì)Carry-Lookahead Adder[2-3]的分析可以發(fā)現(xiàn)進(jìn)位的產(chǎn)生不必等到加法運(yùn)算結(jié)束，即：
  
    完整的電路圖如圖3所示,。

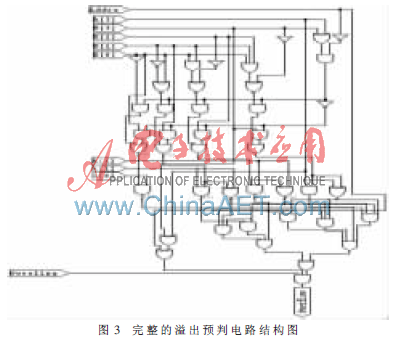
    通過比較圖3與圖1的電路結(jié)構(gòu)發(fā)現(xiàn),，改進(jìn)的溢出判斷邏輯電路圖在結(jié)構(gòu)上要精簡(jiǎn)許多。
2.4 邏輯驗(yàn)證
    電路的功能驗(yàn)證利用TSPICE實(shí)現(xiàn),，仿真得到的波形如圖4所示,。在仿真波形圖中，從上至下信號(hào)名依次為Overflag,，Adder,，A[3]，A[2],，A[1],，A[0]，B[3],，B[2],，B[1]，B[0]和Overflow,。通過分析仿真波形圖中輸入的A,、B、Adder,、Overflag共17組驗(yàn)證數(shù)據(jù)與輸出信號(hào)Overflow的關(guān)系可以證明該電路能夠正確判斷溢出的產(chǎn)生情況,。

 

 

2.5 延時(shí)比較
    Adder到Overflow的路徑為溢出判斷電路的關(guān)鍵路徑，通過仿真工具TSPICE分別計(jì)算兩種電路結(jié)構(gòu)中關(guān)鍵路徑的延時(shí),，在相同的仿真條件下,，改進(jìn)溢出判斷電路中從Adder到Overflow的延時(shí)為11.697 ns，傳統(tǒng)溢出判斷電路中從Adder到Overflow的延時(shí)為12.232 ns。 
    本文在傳統(tǒng)溢出判斷電路的基礎(chǔ)上,，提出一種改進(jìn)的電路結(jié)構(gòu),，在這種改進(jìn)結(jié)構(gòu)中，不必等到加減法運(yùn)算結(jié)果的產(chǎn)生就能預(yù)先判斷有無溢出現(xiàn)象的發(fā)生,。通過仿真發(fā)現(xiàn),，這種結(jié)構(gòu)在能夠?qū)崿F(xiàn)所需的邏輯功能的基礎(chǔ)上減少了電路規(guī)模，并減少了傳輸延遲,。
參考文獻(xiàn)
[1] 王穎.數(shù)字芯片溢出邏輯電路的設(shè)計(jì)與仿真研究[J].微計(jì)算機(jī)信息,，2010，02（26）：160-163.
[2] OMONDI A R.Computer arithematic systems-algorithms, architecture and implementation[M].Prentice-Hall,，1994.
[3] PARHAMI B.Computer arithmetic-algorithms and hardware designs[M].Oxford University Press,，2000.
[4] 劉杰，易茂祥.6加數(shù)并行加法器及擴(kuò)展接口的研究[J].微電子學(xué)與計(jì)算機(jī),，2009,，12（12）：27-30.

此內(nèi)容為AET網(wǎng)站原創(chuàng)，未經(jīng)授權(quán)禁止轉(zhuǎn)載,。