1 引言
在基于查找表的自適應(yīng)預(yù)失真放大器中,最小均方LMS(1east-mean-square)算法廣泛采用文獻(xiàn)[1-5]所提出的觀點(diǎn)。初始收斂速度、時(shí)變系統(tǒng)跟蹤能力及穩(wěn)態(tài)失調(diào)是衡量自適應(yīng)濾波算法優(yōu)劣的最重要技術(shù)指標(biāo)。LMS算法的缺點(diǎn)是收斂速度慢。為了提高LMS算法的收斂速度,文獻(xiàn)[6]提出改進(jìn)的兩個(gè)方法:輸入信號(hào)去相關(guān)和盡可能增大步長(zhǎng)參數(shù)。對(duì)于輸入信號(hào)去相關(guān)方面,研究了分塊LMS算法,DCT-LMS算法,歸一化LMS算法。而增大步長(zhǎng)參數(shù)方面,發(fā)現(xiàn)子帶自適應(yīng)LMS算法,SVSLMS算法,改進(jìn)的SVSLMS算法。根據(jù)以前的研究:固定步長(zhǎng)的自適應(yīng)濾波算法在收斂速度、時(shí)變系統(tǒng)跟蹤速度與收斂精度方面對(duì)算法步長(zhǎng)因子的要求是相互矛盾的。為解決這一矛盾,提出LMS算法的步長(zhǎng)調(diào)整原則;在初始收斂階段或未知系統(tǒng)參數(shù)發(fā)生變化時(shí),步長(zhǎng)應(yīng)較大,以便有較快的收斂速度和對(duì)時(shí)變系統(tǒng)的跟蹤速度;而在算法收斂后,應(yīng)保持很小的步長(zhǎng)以達(dá)到很小的穩(wěn)態(tài)失調(diào)噪聲。
在深入研究自適應(yīng)算法的基礎(chǔ)上,提出一個(gè)新的變步長(zhǎng)LMS算法并與以前算法相對(duì)比仿真。新算法已用于預(yù)失真放大器仿真并取得良好效果。
2 數(shù)字預(yù)失真放大器
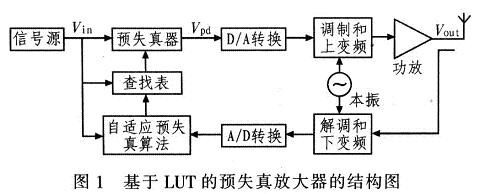
圖1為數(shù)字預(yù)失真放大器的基本結(jié)構(gòu),預(yù)失真器包括查找表和自適應(yīng)預(yù)失真參數(shù)估計(jì),反饋的輸出信號(hào)Vout和輸入信號(hào)Vin經(jīng)自適應(yīng)算法計(jì)算更新查找表中的增益系數(shù),此增益系數(shù)與輸入信號(hào)做乘法運(yùn)算得到預(yù)失真信號(hào)Vpd一般而言,預(yù)失真器要補(bǔ)償?shù)氖怯煞糯笃鞣蔷€性帶來(lái)的幅度非線性失真和相位非線性失真。預(yù)失真器的輸入輸出關(guān)系表示為:
![]()
式中:F(·)為預(yù)失真器的增益函數(shù)。
功率放大器的輸出:
![]()
式中,G(·)為功率放大器的增益函數(shù)。
式(2)代人式(1),則有:
![]()
信號(hào)經(jīng)過(guò)自適應(yīng)預(yù)失真放大器之后其輸出為:

3 查找表的自適應(yīng)算法
LMS算法中,令Rin(n)為輸入信號(hào)的自相關(guān)矩陣。W(n)為抽頭權(quán)向量,那么有:
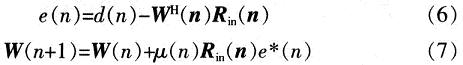
式中:d(n)為期望信號(hào);e(n)為期望信號(hào)與輸出信號(hào)的誤差信號(hào);μ為步長(zhǎng)參數(shù),μ(n)=β(1-exp(-α|e(n)|2))。
LMS算法收斂的條件為:0<μ<1/λmax,λmax是輸入信號(hào)自相關(guān)矩陣的最大特征值。提出改進(jìn)的SVSLMS算法,從而提高LMS算法的收斂速度。
4 新的自適應(yīng)算法
新的自適應(yīng)算法為
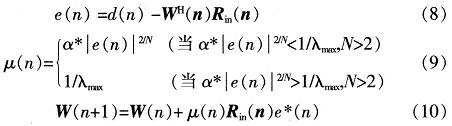
式(9)中μ(n)要滿(mǎn)足0<μ(n)<1/λmax。由于α是人為指定,所以可由試驗(yàn)手段取得,e(n)是未知變量,其初始值無(wú)法估計(jì),所以首先要判斷α*| e(n)|2/N是否小于1/λmax。但是這會(huì)增加時(shí)間復(fù)雜度,如果能夠確認(rèn)α*| e(n)|2/N<1/λmax,比如第一次迭代的e(n)<1,則可直接設(shè)定α為小于1/λmax的值計(jì)算,以便減少時(shí)間復(fù)雜度。
5 仿真結(jié)果
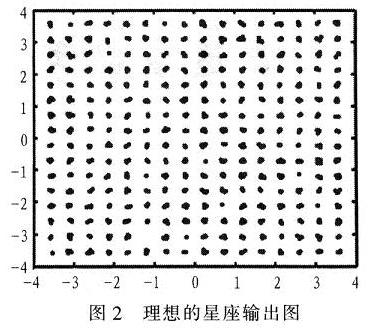
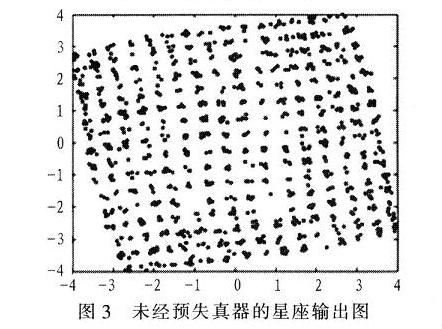
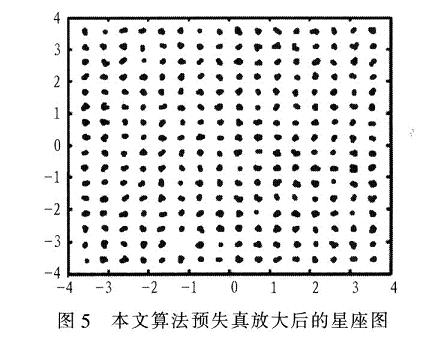
用MATLAB搭建了一個(gè)自適應(yīng)預(yù)失真放大器的模型,放大器使用saleh模型。輸入信號(hào)為256QAM信號(hào),分別對(duì)SVSLMS改進(jìn)型算法和該新算法進(jìn)行仿真對(duì)比,其中SVSLMS改進(jìn)型算法的參數(shù)取值為β=1,α=10,該新算法參數(shù)取值為α=2,N=5。迭代500次的結(jié)果如圖2~圖5。其中,圖2是理想的功放輸出星座圖;圖3是未經(jīng)預(yù)失真器的功放輸出星座圖:圖4是采用改進(jìn)的SVSLMS算法的預(yù)失真放大器的輸出星座圖;圖5是采用新算法的預(yù)失真放大器的輸出星座圖。通過(guò)仿真可知,該新算法對(duì)預(yù)失真放大器的改進(jìn)明顯優(yōu)于SVSLMS改進(jìn)型算法。

6 結(jié)論
提出一個(gè)新的變步長(zhǎng)LMS算法,通過(guò)誤差的平方函數(shù)控制步長(zhǎng)的變化,有很好的收斂特性,用MATLAB搭建了預(yù)失真放大器的仿真系統(tǒng)。仿真表明:在進(jìn)行500次迭代計(jì)算時(shí)該新算法對(duì)預(yù)失真放大器非線性特性的改進(jìn)明顯優(yōu)于改進(jìn)的SVSLMS算法。

