0 引言

    2006年,，CANDES D E等人提出了壓縮感知（Compressed Sensing，CS）理論^[1],，CS理論利用與表達(dá)基不相干的觀測矩陣,，以低于奈奎斯特的采樣速率非自適應(yīng)地采樣可稀疏表示的信號，得到低維的離散信息矢量,，該信息矢量包含了原始信號的全部信息,，然后通過非線性重建算法完美地重建信號。

    壓縮感知理論主要包含了三大核心部分：信號的稀疏表示,、測量矩陣的構(gòu)造和信號重構(gòu)算法的設(shè)計,。在壓縮感知理論的三個核心問題中，如何設(shè)計并用硬件實現(xiàn)根據(jù)離散信息樣點準(zhǔn)確重構(gòu)原始信號的行之有效的算法是該理論中較為重要的一環(huán),。目前,，壓縮感知信號重構(gòu)算法主要分為兩類：基于凸松弛的優(yōu)化算法，如基追蹤（Basis Pursuit,，BP）算法,；基于貪婪迭代的匹配追蹤算法，如OMP算法^[2],。這兩類算法各有優(yōu)缺點：凸松弛算法具有很好的魯棒性,，然而由于需要將求解問題轉(zhuǎn)化為線性規(guī)劃問題，計算量大,，信號重構(gòu)效率低,；貪婪算法雖然不具有強(qiáng)保證性，但實現(xiàn)簡單,，重構(gòu)效率高,，在工程應(yīng)用中得到廣泛使用^[3]。

    首次對壓縮感知恢復(fù)算法進(jìn)行VLSI設(shè)計是在參考文獻(xiàn)[4]中,，而之后,，有文獻(xiàn)進(jìn)行優(yōu)化設(shè)計。參考文獻(xiàn)[5]根據(jù)OMP算法必須按照特定順序執(zhí)行這一特征,，采用資源復(fù)用技術(shù),，提高了資源利用率。參考文獻(xiàn)[6]設(shè)計了一個快速求逆平方根算法，在矩陣分解部分采用QR算法,。參考文獻(xiàn)[7]對OMP算法進(jìn)行優(yōu)化,，減少了計算延時。參考文獻(xiàn)[8]同時進(jìn)行了OMP算法和AMP算法的VLSI設(shè)計,。本文先對OMP算法進(jìn)行理論分析,，然后對OMP算法進(jìn)行改進(jìn)，通過增加一個閾值來減少乘法運算次數(shù),，使運算速度更快,。在矩陣分解部分采用ACD方法避免開方運算，同時在硬件實現(xiàn)上也進(jìn)行了相應(yīng)的優(yōu)化,。仿真結(jié)果驗證了設(shè)計的可行性,。

1 OMP算法

1.1 基本OMP算法

    在壓縮感知中，原始信號x的稀疏度為k,，觀測矢量y是所采集的數(shù)據(jù),，y可通過測量矩陣Φ與x相乘而得。本設(shè)計的目的是在已知y和Φ的前提下恢復(fù)出x,。OMP算法主要分為兩部分,，即尋找稀疏矢量中非零元素的位置和計算非零元素的值。

    在OMP算法中殘差r是一個很關(guān)鍵的參數(shù),，殘差是通過當(dāng)前選取的列向量和原始信號的線性組合不能對壓縮測量值進(jìn)行表示的部分,。

1.2 改進(jìn)OMP算法

    令原始信號x的稀疏度為k，測量矩陣Φ大小為M×N,，那么y為M維的離散信息矢量,。本文提出一種新的方法，即加閾值法,，通過添加一個閾值來減少乘法運算次數(shù),，閾值定為內(nèi)積和的平均值的α倍，內(nèi)積小于閾值的那些列在下一次迭代中不再求內(nèi)積,。每次迭代計算后都要對閾值進(jìn)行更新,。信號估計的均方誤差隨著α的增大而增大，當(dāng)α為0時均方誤差最小,。改進(jìn)的OMP算法步驟如下：

2 計算步驟

    本文利用硬件實現(xiàn)重構(gòu)長度N=256,、稀疏度k=8的原始信號，觀測矢量長度M=64,。

    改進(jìn)后的OMP算法可分為4個模塊。第1個模塊對應(yīng)重建過程的第(1)和第(2)步,，也就是在剩余列的集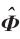中尋找對殘差貢獻(xiàn)最大的列為最匹配原子,。

    第2個模塊對應(yīng)重建過程的第(3)步，即計算新殘差，為下次迭代做準(zhǔn)備,。

    第3個模塊對應(yīng)重建過程的第(4)和第(5)步,，即計算新的閾值并除去剩余列的集中和殘差求內(nèi)積小于閾值的列。求閾值前要先求內(nèi)積的平均值,。第t次迭代的內(nèi)積平均值可用以下公式計算：

    為解決對Φ的列的定位問題,，用一個256位的標(biāo)志位來追蹤Φ的列，標(biāo)志位的第i位對應(yīng)Φ的第i列,。在第i列和殘差求內(nèi)積后,，下一個時鐘和殘差求內(nèi)積的就是下一個標(biāo)志位為非零所對應(yīng)的列，跳過標(biāo)志位為零對應(yīng)的列,。開始前先把標(biāo)志位的每一位全部初始化成1,，在每一次迭代之后對標(biāo)志位進(jìn)行更新。

    第4個模塊對應(yīng)重構(gòu)過程的第(7)步,，求解非零元素的值,，即解決最小二乘問題。對于這類運算一般用Moore-Penrose偽逆的方法求解：

    求出C的逆矩陣后,，就可以求得原始信號的估計：

    由于OMP算法的迭代性質(zhì),，4個模塊是不能并行執(zhí)行的，只能每個模塊依次執(zhí)行,。

3 硬件設(shè)計

    硬件電路主要由以上4個模塊組成,，分為兩個部分。整體硬件電路如圖1所示,。

    首先用觀測矢量y對殘差r進(jìn)行初始化,。y用寄存器組存儲，而觀測矩陣Φ用多個RAM存儲,，這樣就能在一個時鐘內(nèi)讀出y的所有值和Φ的一列值,。數(shù)據(jù)用24位定點數(shù)表示，10位整數(shù),，14位小數(shù),。設(shè)計64個24位乘法器并行工作來求內(nèi)積，然后找到內(nèi)積最大值來更新,。矩陣的大小變化從N×1～N×8,。

    每次迭代后會把Φ中和殘差內(nèi)積小于閾值的列過濾掉，根據(jù)式(9),、(10)和(11),，剩余列的集中的每一列和殘差的內(nèi)積都送到累加器進(jìn)行求和，然后通過求內(nèi)積平均值求得閾值,。閾值參數(shù)α設(shè)置為一個常數(shù),。

    256位標(biāo)志位作為Φ的地址尋址,，標(biāo)志位每一位對應(yīng)Φ每一列，初始化為所有位為1,。每次迭代后對標(biāo)志位進(jìn)行更新,，把Φ中和殘差內(nèi)積小于閾值的列所對應(yīng)的標(biāo)志位賦為零，否則保持為1,。然后在下一次迭代時跳過標(biāo)志位為零所對應(yīng)的Φ的列,，也就是直接用下一個非零標(biāo)志位所對應(yīng)的列與殘差進(jìn)行求內(nèi)積。通過把標(biāo)志位的前32位送到一個32位前導(dǎo)零計算器可以找出下一個非零位,。

    在尋找非零元素位置的部分迭代8次后,，就開始計算非零元素的值。首先要計算矩陣可通過以下等式計算：

    此處復(fù)用之前的64個乘法器,。C是一個對稱矩陣,，所以只需要計算C的對角線上8個元素和對角線下半部（或上半部）的28個元素。

    然后要對C進(jìn)行交替的柯列斯基分解,，矩陣分解要求出下三角矩陣L和對角矩陣D,。從式(13)和(14)可以看出，L和D是相互依存的,，必須以特定的順序計算,。本設(shè)計中稀疏度k=8，L和D可以按照圖2箭頭所指順序計算,。設(shè)計7個乘法器并行計算D中的元素,，那么每計算一個元素需要一個時鐘周期。計算D^-1時采用參考文獻(xiàn)[9]的方法進(jìn)行除法運算,。由于L的同一列的各個元素并不是相互依存的,，所以求L的每一列值都設(shè)計為并行計算各個元素，那么每一列的計算只需要一個時鐘周期,。

    矩陣L的求逆需要迭代進(jìn)行,，如式(18)：

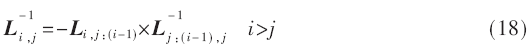
    由于L的逆矩陣的各列的各個元素是相互依存的，所以列和列可以并行運算,，每一列要按照特定的順序運算,，那么計算L^-1需要7個時鐘周期。

    求C^-1=(L-1)^T×D^-1×L^-1時可以先求A=(L^-1)^T×D^-1,，然后再計算C^-1=A×L^-1,。

4 仿真及結(jié)果分析

    考慮到兩個模塊的最大運行頻率不一樣，本設(shè)計在尋找非零元素部分采用85 MHz的時鐘,，在求解非零元素值部分采用65 MHz的時鐘,。為了進(jìn)行更好的對比，在MATLAB上用相同的算法,、測量矩陣和觀測矢量來重構(gòu)原始估計值,。當(dāng)α=0.25時,，軟件和硬件的重構(gòu)結(jié)果進(jìn)行歸一化后的對比如圖3所示。

    當(dāng)α取值為零時,，尋找非零元素部分共需要2 100個時鐘周期，而僅僅是計算內(nèi)積就需要256×8=2 048個時鐘周期,，計算非零元素部分共需要110個時鐘周期,，總的重構(gòu)時間為26.40 μs。當(dāng)α取值為0.25時,，計算內(nèi)積所需減少到約1 300個時鐘周期,，總的重構(gòu)時間減少到約16.99 μs。在相同條件下,，參考文獻(xiàn)[7]重構(gòu)時間為17.61 μs,。而在參考文獻(xiàn)[4]中，測量矩陣維數(shù)為32×128,，觀測向量維數(shù)為32×1,，原始信號的稀疏度為5，總的重構(gòu)時間就需要24 μs,。

    但是改進(jìn)OMP算法歸一化誤差會隨著α的增大而增大,，當(dāng)α取值為零時，歸一化均方誤差為0.001 5,，取α=0.25時,，歸一化均方誤差增加到0.007 1。

5 結(jié)論

    本文采用一種閾值法,，使得OMP恢復(fù)算法的求內(nèi)積次數(shù)大大減少,，從而縮短了信號重構(gòu)所需要的時間，提高了恢復(fù)速率,。同時,，本文在硬件結(jié)構(gòu)設(shè)計上也進(jìn)行了一些優(yōu)化，較好地平衡了占用資源和運算時間,。本設(shè)計采用VHDL對改進(jìn)的OMP算法進(jìn)行了RTL級描述,，在Quartus II上針對Altera公司的Cyclone II EP2C70F672C6進(jìn)行設(shè)計和仿真，結(jié)果表明信號能夠以更少的重構(gòu)時間較好地恢復(fù),。

參考文獻(xiàn)

[1] DONOHO D L.Compressed sensing[J].Information Theory,，IEEE Trans. on，2006,，52(4)：1289-1306.

[2] TROPP J A,，GILBERT A C.Signal recovery from random measurements via orthogonal matching pursuit[J].Information Theory，IEEE Trans.on,，2007,，53(12)：4655-4666.

[3] 趙貽玖.稀疏模擬信號壓縮采樣與重構(gòu)算法研究[D].成都：電子科技大學(xué),，2012.

[4] SEPTINUS A，STEINBERG R.Compressive sampling hardware reconstruction[C].Circuits and Systems(ISCAS),，Proc.of 2010 IEEE International Symposium on.IEEE,，2010：3316-3319.

[5] BLACHE P，RABAH H,，AMIRA A.High level prototyping and FPGA implementation of the orthogonal matching pursuit algorithm[C].Information Science,，Signal Processing and their Applications(ISSPA)，2012 11th International Conference on.IEEE,，2012：1336-1340.

[6] STANISLAUS J L V M,，MOHSENIN T.High performance compressive sensing reconstruction hardware with QRD process[C].Circuits and Systems(ISCAS)，2012 IEEE International Symposium on.IEEE,，2012：29-32.

[7] STANISLAUS J,，MOHSENIN T.Low-complexity fpga implementation of compressive sensing reconstruction[C].International Conference on Computing，Networking and Communications.2013.

[8] BAI L,，MAECHLER P,，MUEHLBERGHUBER M，et al.High-speed compressed sensing reconstruction on FPGA using OMP and AMP[C].Proc.19th Int.Conf.Electronics,，Circuits and Systems(ICECS),，Dec.2012：53-56.

[9] 周殿鳳，王俊華.基于FPGA的32位除法器設(shè)計[J].信息化研究,，2010(3)：26-28.