摘  要： 針對粒子群優(yōu)化算法的鄰域拓撲結構對算法性能有重要影響、PSO算法在CPU上求解最優(yōu)化問題時計算效率低下這兩點,，分析了鄰域拓撲結構改變時PSO算法的并行特征,，實現(xiàn)了環(huán)形和星形拓撲結構的PSO算法在統(tǒng)一計算設備架構上的尋優(yōu)過程。分別在CPU和GPU上用兩種PSO算法對7個benchmark測試函數(shù)進行求解,。程序仿真結果顯示,，基于CUDA的PSO算法計算效率均大大高于CPU；同時發(fā)現(xiàn),，GPU顯著地加快了星形結構PSO算法的收斂速度,，而對環(huán)形結構PSO算法影響不大。

　　關鍵詞： 粒子群優(yōu)化算法,；統(tǒng)一計算設備架構,；鄰域拓撲結構；計算效率

　　料子群優(yōu)化PSO（Particle Swarm Optimization）算法最早于1995年由EBERHART博士和KENNEDY博士提出[1],，由于實現(xiàn)容易,、精度高和收斂快等優(yōu)點，引起了學術界的重視,，并且在實際問題的解決中展示了其優(yōu)越性,。

　　近年來，針對基本PSO算法易陷入局部極值,，求解某些問題時精度不足的缺點[1],，研究人員們提出了各種改進算法，包括參數(shù)調整[2]，改變搜索網(wǎng)絡空間[3-4],，混合其他算法[5-6]等,。目前,，PSO算法作為優(yōu)化工具成功應用于多個領域,，如無線傳感器網(wǎng)絡（WSN）覆蓋問題的研究[7],。PSO算法性能對社會網(wǎng)絡結構具有強烈的依賴性[1,，3-4],，鄰域拓撲結構的改變對PSO算法的收斂性有重要作用。

　　求解高維復雜函數(shù)時,，傳統(tǒng)PSO算法因需處理大量數(shù)據(jù),，致計算效率過低,，研究人員基于算法本身特性提出了各種并行PSO算法[8-10]，均取得了至少10倍以上的加速比,。GPU起初只是負責圖形渲染，直到2006年公布了GeForce系列GPU,，GPU才開始應用于通用計算[11],。GPU和CPU的協(xié)同工作，現(xiàn)已被廣泛應用于石油勘探[12],、生物計算[13]等領域,。本文借助于CUDA平臺，對鄰域拓撲結構發(fā)生變化時的PSO算法進行了探究,，驗證了并行計算平臺的高效性,，同時探索了并行計算平臺對星形和環(huán)形PSO算法收斂性的影響。

　　1 標準PSO算法

　　PSO算法[1]源于對鳥類覓食過程的模擬：將每只鳥看成D維空間中沒有質量和體積的微粒,，這些微粒以一定速度飛行,，速度由個體的飛行經(jīng)驗和群體的飛行經(jīng)驗進行動態(tài)調整。

　　標準PSO算法的速度和位置更新方程如下：

　　v（t+1）=?棕v（t）+c1×r1×（p（t）-x（t））+c2×r2×（pg（t）-x（t））（1）

　　x（t+1）=x（t）+v（t+1）（2）

　　其中,，v（t）=（v1,，v2，…,，vd）為當前微粒在第t代的速度,；為慣性權重,，文中取?棕=0.5；c1為認知系數(shù),；c2為社會系數(shù),，通常取c1=c2=2；r1,，r2為服從均勻分布的0~1之間的隨機數(shù),；p（t）=（p1,，p2，…,，pd）為當前微粒的歷史最優(yōu)位置,；x（t）=（x1，x2,，…,，xd）為當前微粒在第t代的位置；p（t）=（pg1,，pg2,，…，pgd）為群體歷史最優(yōu)位置,。典型的標準PSO算法的尋優(yōu)流程如圖所示,。

　　2 PSO算法的拓撲結構

　　為提高PSO算法的性能,，參考文獻[3-4]提出了不同類型的拓撲結構,，包括動態(tài)拓撲和靜態(tài)拓撲。KENNEDY J對在各種靜態(tài)鄰域結構中的PSO算法性能進行了分析[1],，認為星型,、環(huán)型和Von Neumann拓撲適用性最好，并稱小鄰域的PSO算法在復雜問題上性能較好,，大鄰域的PSO算法在簡單問題上性能更好,，在本實驗中得到進一步論證,。

　　分別為星形和環(huán)形拓撲圖,，星形PSO算法中所有粒子全部相聯(lián)，每個粒子都可以同除自己以外的其他粒子通信,，以共享整個群體最佳解,；環(huán)形網(wǎng)絡結構中每個粒子跟它的n個鄰居通信，每個粒子向鄰域內(nèi)的最優(yōu)位置靠攏,，來更新自己的位置,，可見,，每個粒子只是共享所在鄰域內(nèi)的最優(yōu)解，即局部最優(yōu),，而全局最優(yōu)流動在整個環(huán)形網(wǎng)絡中,。

　　除以上兩種基本拓撲結構外，還有馮諾依曼型,、輪型,、金字塔型,、四聚類型結構和一些基于這幾種結構的改進拓撲[1,，3-4]，其中普遍認為馮諾依曼結構在解決大多數(shù)問題時要優(yōu)于其他結構[1],。當然,，并不存在對所有問題都適用的最好拓撲。

　　3 CUDA及CUDAC

　　3.1 CUDA編程模型

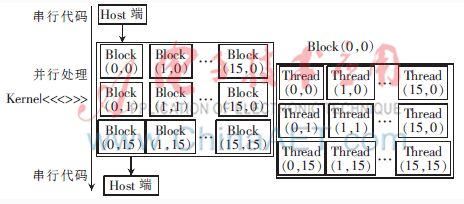
　　統(tǒng)一計算設備架構CUDA（Compute Unified Device Arch-itecture）,，在CUDA編程模型中,，CPU為主機（Host）端，GPU作為協(xié)處理器,，兩者各自擁有獨立的存儲器和各自的編譯器[14-15],。一個完整的CUDA編程模型如圖4所示：程序執(zhí)行始于主機，止于主機,。圖中Kernel并行處理部分為基于單指令多線程SIMD（Single Instruction Multiple Thread）計算模型,，線程被CUDA組織成3個不同的層次：線程（Thread）、線程塊（Block）以及線程格（Grid）,。

　　3.2 CUDA存儲器模型

　　線程在執(zhí)行指令時,，需訪問處于不同存儲器的數(shù)據(jù)，而對各類存儲器的訪問速度差異很大[13],。CUDA存儲器分為3層：（1）私有本地存儲器（private local memory）,，容量小，訪問速度快,；（2）全局存儲器（global memory）,，所有線程都可訪問,，訪問速度慢,；（3）共享存儲器（shared memory），屬于片上存儲器,，訪問速度與寄存器相當,，定義共享類型變量時需使用限定符__shared__,。

　　3.3 CUDA C

　　CUDA C是對C的擴展,，為程序員提供了一種用C語言在設備上編寫代碼的編程方式,。主要擴展[14-15]：（1）引入__device__，__host__和__global__3個限定符,，限定函數(shù)調用和執(zhí)行的位置；（2）引入4個內(nèi)置變量,，blockIdx,，threadIdx，gridDim和blockDim,；（3）引入<<<>>>運算符,，內(nèi)含4個參數(shù),，主要用于設置線程格和線程塊的尺寸,；（4）擴展了一些數(shù)學函數(shù)庫,，如CURAND[16]。

　　4 基于CUDA的PSO算法

　　4.1 PSO算法的并行編程

　　群體中各粒子只在更新全局最優(yōu)時互相交換信息,，其他步驟均相互獨立,。獲取歷史最優(yōu)時,，一個線程對應一個粒子,，各線程同時調用適應函數(shù)；更新位置和速度時,，一個線程對應粒子的每一維；均按線程索引來讀取數(shù)據(jù)并處理,。

　　主機端初始化粒子的位置和速度,，將數(shù)據(jù)從CPU復制到GPU上，在設備上迭代尋優(yōu),，最后將最優(yōu)解復制到CPU輸出。表1列出了實現(xiàn)各部分功能的函數(shù)，獲取全局最優(yōu)值時,，星形結構可以通過線程歸約比較獲取全局最優(yōu)，環(huán)形結構由于多鄰域而相對復雜,，在后續(xù)部分詳述。

　　4.2 環(huán)形PSO算法尋優(yōu)過程

　　星形PSO算法獲取全局最優(yōu)較為簡單,，不作分析，環(huán)形PSO算法在獲取局部最優(yōu)時，文中設定每個粒子只有左右兩個鄰居,。在編寫該部分程序時,，設置讓相鄰線程訪問索引間隔為3的共享內(nèi)存中的數(shù)據(jù),，這種方法避開了bank沖突,，但以時間消耗作為代價。各線程具體負責找出粒子的歷史最優(yōu)值.

　　找出歷史最優(yōu)值的方式有以下兩種情形（其中N為粒子規(guī)模）：

　?。?）N%3=0時,，各線程按圖5所示處理相應的數(shù)據(jù)，3次并行運行即可得到每個粒子在其鄰域內(nèi)的局部最優(yōu),。

　?。?）N%3≠0時，將圖5中N令為N-N%3,，按情形（1）可以得到0~N-N%3-1號粒子在其鄰域內(nèi)的局部最優(yōu),，再對余下的1或2個粒子依次找出其鄰域內(nèi)局部最優(yōu)。

　　由于環(huán)型PSO算法有N個局部最優(yōu)值，設備上尋優(yōu)結束后,，需將N個局部最優(yōu)從GPU復制到CPU進行比較,，最后輸出全局最佳解。

　　4.3 CUDA程序性能優(yōu)化

　　GPU性能雖然出色,，但很大程度上受限于算法本身[15],。在CUDA的使用中，數(shù)據(jù)結構和對內(nèi)存的訪問對GPU性能有極大地影響,，有時甚至起決定性作用,。文中實驗程序對CUDA性能優(yōu)化，主要考慮了以下4個方面：（1）最大化并行性,；（2）優(yōu)化內(nèi)存訪問以獲得最大的帶寬；（3）優(yōu)化指令使用以獲得最大指令的吞吐量,；（4）線程塊和線程數(shù)的設置,，實驗表明當設置線程塊數(shù)為32，每個塊中線程數(shù)為256時獲得最高效率,。

　　5 結論分析

　　5.1 計算時間對比

　　在獨立的CPU和CPU+GPU并行計算平臺上,，分別對以下7個benchmark函數(shù)進行了測試,，其中D表示粒子的維數(shù)，xi的范圍表示搜索空間,。

　　（1）Sphere函數(shù)

　　f1（x）=x,，|xi|≤15（3）

　　（2）Ackley函數(shù)

　　f2（x）=20exp-0.2-

　　expcos（2πoi）+20+e）,，|xi|≤15（4）

　　（3）Schwefel函數(shù)

　　f3=418.928×D-xisin（）,，|xi|≤500（5）

　?。?）Levy函數(shù)

　　f4=sin2（πyl）+[（yi-1）2×（1+10sin2（πyi+1））]+（yD-1）2（1+sin2（2π2n））   yi=1+，|xi|≤10（6）

　?。?）Griewank函數(shù)

　　f5+1,，|xi|≤600（7）

　?。?）Rastrigin函數(shù)

　　f6=10cos（2ππi）+10]，|xi|≤5.12（8）

　?。?）Rosenbrock函數(shù)

　　f7=xi+12+（xi-1）2,，-5≤xi≤10（9）

　　星形結構和環(huán)形結構PSO算法在CPU和CUDA上的運行時間如表2所示，測試時取粒子數(shù)為1 000,，粒子維數(shù)為50,，迭代次數(shù)為5 000。表中數(shù)據(jù)經(jīng)多次測試,，取均值得到,。表2顯示，相同條件下,，GPU和CPU上的環(huán)型PSO算法均略慢于星型,。還可以看到，函數(shù)越復雜,，加速比越大,。并經(jīng)多次測試比較發(fā)現(xiàn)，迭代次數(shù)增加,，加速比增大,。表3為迭代次數(shù)為10 000時的函數(shù)f1~f7求解時間,。

　　表4列出了維數(shù)50，粒子數(shù)為500,，迭代次數(shù)10 000時,，星形和環(huán)形PSO算法求解函數(shù)f1~f7的時間。對比表3和表4,，可知粒子數(shù)為500時的加速比明顯要低于粒子數(shù)為1 000時,，對比表2和表4發(fā)現(xiàn)，盡管迭代變大,，而粒子數(shù)較大時加速比越大,，說明種群規(guī)模對加速比的影響要大于迭代數(shù)。這正體現(xiàn)了PSO算法粒子的并行性,，粒子規(guī)模越大,，在GPU上的并行處理越具優(yōu)勢；反而當粒子數(shù)較小時,，由于并行前后CPU和GPU之間的通信所需時間隱藏被弱化,，此時在GPU上運行不占任何優(yōu)勢，有時甚至差于CPU,。進一步說明了GPU適用于大規(guī)模數(shù)據(jù)并行運算中,。

　　5.2 收斂性對比

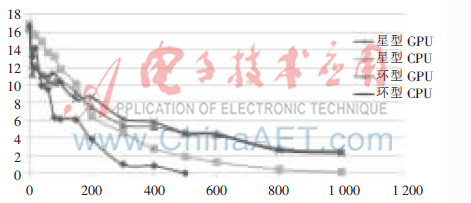
　　除計算效率極大提升外，GPU還加快了星型PSO算法的收斂速度,。圖6描繪了兩種結構PSO算法在CPU和GPU上求解函數(shù)f2的收斂曲線,，實驗取粒子數(shù)500，維數(shù)50,，迭代次數(shù)從0逐漸增大,，基于算法本身的隨機性，記錄最優(yōu)解數(shù)據(jù)時對指定的迭代數(shù)循環(huán)100次,，取其平均值,。

　　可見，迭代早期兩種結構PSO算法的收斂速度相差不大,，而隨著迭代增大，星形PSO算法的收斂速度明顯加快,。實驗結果還表明,，對于環(huán)形PSO算法，GPU并未加快收斂,，而對于星形結構,，GPU明顯加快了算法的收斂速度。其余6個benchmark函數(shù)的求解也表明,，GPU確實加快了星形PSO算法的收斂速度,。

　　本實驗GPU顯卡型號為NVIDIA GeForce GT 630M，CUDA計算能力為2.1。圖表中僅列出了粒子數(shù)和迭代數(shù)改變時加速比的變化情況,，維數(shù)的改變對加速比也有重要影響,。PSO算法的這種并行策略，在遺傳算法,、蟻群算法,、文化算法及一些混合算法中具有較強的通用性，可以很大地提高搜索效率,。PSO作為一種新興進化算法,，各種研究工作種類繁多，在函數(shù)優(yōu)化,、多目標優(yōu)化,、約束優(yōu)化、算法結構改進,、應用工程領域等方面[17]均取得重大成果,，而CUDA作為一種新興計算平臺，必將推動PSO算法的發(fā)展,。

　　參考文獻

　　[1] KENNEDY J,， EBERHART R C. Particle swarm optimiza-tion[C]. Proceedings of IEEE International Conference on Neural Networks， Piscataway,， 1995：1942-1948.

　　[2] 延麗平,，曾建潮.具有自適應隨機慣性權重的PSO算法[J].計算機工程與設計，2006,，27（24）：4677-4679,，4706.

　　[3] 楊道平.粒子群算法鄰域拓撲結構研究[J].中國高新技術企業(yè)評價，2009,，（16）：36-37.

　　[4] 姚燦中,，楊建梅.基于網(wǎng)絡鄰域拓撲的粒子群優(yōu)化算法[J].計算機工程，2010,，36（19）：18-20.

　　[5] 王志,，胡小兵，何雪海,，等.一種新的差分與粒子群算法的混合算法[J].計算機工程與應用,，2012，48（6）：46-48.

　　[6] 易文周,，張超英,，王強，等.基于改進PSO和DE的混合算法[J].計算機工程,，2010,，36（10）：233-235.

　　[7] 史朝亞,，樊春麗.基于PSO算法的無線傳感器網(wǎng)絡覆蓋的研究[D].南京：南京理工大學，2013.

　　[8] You Zhou,， Ying Tan. GPU-based parallel part- icle swarm optimization[J]. Proceedings of IEEE International Conference on Evolutionary Computation,， 2009：1493-1500.

　　[9] LUCAS DE P VERONESE， RENATO A K-ROHLING. Swarm′s flight： accelerating the particles using C-CUDA[C]. Proceedings of IEEE International Conference on Evolutionary Computation,，2009：3264-3270.

　　[10] 蔡勇,，李光耀，王琥.基于CUDA的并行粒子群優(yōu)化算法的設計與實現(xiàn)[J].計算機應用研究,，2013,，30（8）：2415-2418.

　　[11] 劉金碩，劉天曉,，吳慧,，等.從圖形處理器到基于GPU的通用計算[J].武漢大學學報（理學版），2013,，59（2）：198-199.

　　[12] 張兵,，趙改善，黃俊,，等.地震疊前深度偏移在CUDA上的實現(xiàn)[J].勘探地球物理進展,，2008，31（6）：427-430.

　　[13] 余林彬,，徐云.基于CUDA的高性能計算研究及生物信息學應用[D].合肥：中國科學技術大學,，2009.

　　[14] NVIDIA. NVIDIA CUDA Programming Guide Version 2.3.1[EB/OL].https：//developer.nvidia.com/category/zone/cuda-zone[2007].

　　[15] 張舒，褚艷利,，趙開勇,，等.GPU高性能運算之CUDA[M].北京：中國水利水電出版社，2009.

　　[16] NVIDIA. NVIDIA CUDA CURAND Library[EB/OL]. http：//docs.nvidia.com/cuda/curand/index.html[2010].

　　[17] 倪慶劍,，邢漢承,，張志政，等.粒子群優(yōu)化算法研究進展[J].模式識別與人工智能,，2007,，20（3）：350-357.