文獻(xiàn)標(biāo)識(shí)碼: A
文章編號(hào): 0258-7998(2015)05-0077-04
0 引言
電機(jī)振動(dòng)信號(hào)的觀測(cè)數(shù)據(jù)中包含著大量的特征信息,為了能有效地提取有用的特征信息,,需要對(duì)電機(jī)振動(dòng)信號(hào)進(jìn)行降噪處理,。傅里葉變換不能逼近電機(jī)振動(dòng)信號(hào)的局部信息,不適用于電機(jī)振動(dòng)信號(hào)的降噪處理[1],。小波函數(shù)具有局部分析功能,,能夠非常好地逼近信號(hào)的細(xì)節(jié)特征,便于電機(jī)特征信息的提取,。文獻(xiàn)[2]提出的快速小波分解算法使得小波在多個(gè)領(lǐng)域得到了廣泛應(yīng)用,,在此基礎(chǔ)上,小波閾值降噪也得到快速發(fā)展,。
文獻(xiàn)[3]提出了小波閾值降噪算法,,其原理是信號(hào)和噪聲在小波域中呈現(xiàn)著不同表現(xiàn)形式,隨著分解尺度的增加,,噪聲系數(shù)的幅值快速衰減逼近于零,,而真實(shí)信號(hào)系數(shù)的幅值保持不變[4]。在閾值降噪的過(guò)程中,,閾值和閾值函數(shù)的選擇是重要的一步,。目前Bayes閾值是比較受歡迎的閾值選取方法之一。
Bayes閾值降噪的原理是在假設(shè)小波系數(shù)服從廣義高斯分布的前提下,,通過(guò)最小化貝葉斯風(fēng)險(xiǎn)估計(jì)得到優(yōu)化閾值,,這是目前很多專(zhuān)家學(xué)者選擇較多的閾值選取方法之一[5,6],。本文同樣選用Bayes閾值,,根據(jù)不同分解尺度上信號(hào)和噪聲能量分布不同的特點(diǎn)對(duì)Bayes閾值進(jìn)行改進(jìn),,這樣閾值的選擇更符合噪聲在各層的分布情況[7]。同時(shí),,由于硬閾值函數(shù)是一種不連續(xù)函數(shù),,導(dǎo)致重構(gòu)的信號(hào)具有振蕩性,軟閾值函數(shù)對(duì)信號(hào)作收縮處理與信號(hào)的真實(shí)值存在偏差[8,,9],。針對(duì)上述不足,本文提出改進(jìn)的閾值函數(shù)算法,,使用改進(jìn)閾值函數(shù)結(jié)合新閾值對(duì)小波系數(shù)進(jìn)行修正,,實(shí)現(xiàn)電機(jī)振動(dòng)信號(hào)的有效提取。
1 小波閾值降噪
小波分析方法是一種靈活的局域化時(shí)頻分析方法,。利用多分辨分析放大特性逐步細(xì)化故障信號(hào)頻譜,,發(fā)揮時(shí)域頻域局部化的性能,使故障特征信息明顯表現(xiàn)出來(lái),,便于觀察分析,。
1.1 小波閾值降噪原理
理論分析認(rèn)為,含噪信號(hào)的真實(shí)值與噪聲的小波系數(shù)在小波空間內(nèi)有不同分布,,對(duì)含噪信號(hào)進(jìn)行小波分解后,,噪聲主要集中在高頻的小波系數(shù)中,通過(guò)設(shè)置閾值可將含噪部分去除,,最后對(duì)信號(hào)重構(gòu),,即達(dá)到對(duì)信號(hào)降噪的目的[10],。假設(shè)含噪的電機(jī)振動(dòng)信號(hào)為s,,滿足:

小波閾值降噪一般步驟如圖1所示。其中,,最主要的是閾值和閾值函數(shù)選取,,也就是本文研究的核心算法。

1.2 常用閾值選取方法
目前常用的小波降噪閾值選取方法有4種:固定閾值,、無(wú)偏似然估計(jì)閾值,、啟發(fā)式閾值和極大值極小值閾值。但這些閾值估計(jì)方法都不是最優(yōu)的,,工程中應(yīng)用較多的固定閾值在噪聲較多時(shí)降噪效果明顯,,無(wú)偏似然估計(jì)對(duì)高頻信息保留較多,啟發(fā)式閾值與極大極小閾值在信號(hào)的高頻信息較少包含噪聲時(shí)比較有效[11],。因此需要找到針對(duì)不同含噪信號(hào)的最佳閾值,。
2 改進(jìn)閾值算法
文獻(xiàn)[12]研究指出,電機(jī)故障信號(hào)的小波系數(shù)服從廣義高斯分布,,滿足Bayes估計(jì)條件,。
貝葉斯閾值是采用貝葉斯統(tǒng)計(jì)理論推導(dǎo)得到的[13],,對(duì)于某一給定的高頻信號(hào),閾值選擇為:

因?yàn)樵肼晫?duì)應(yīng)的小波系數(shù)在每一個(gè)尺度上隨機(jī)均勻分布,,隨著分解尺度的增加其幅值在減小,,所以本文將閾值取為:

其中,j為分解尺度,。隨著j的增加,,閾值σ減小,與改進(jìn)之前相比,,更符合噪聲在各層的分布情況,。因此,用該閾值降噪,,降噪效果更好,。
對(duì)式(2)的σn,采用中值估計(jì)[3]:

3 改進(jìn)閾值函數(shù)
以往的小波貝葉斯閾值降噪,,常選用硬閾值函數(shù)和軟閾值函數(shù),,但存在固定偏差和不連續(xù)性等問(wèn)題。文獻(xiàn)[14]中提出了半軟閾值函數(shù),,表達(dá)式為:

其中,,δ為閾值,ω為小波系數(shù),,ω′為閾值處理后的小波系數(shù),,α是范圍在(0,1)的系數(shù),。
半軟閾值介于軟,、硬閾值方法之問(wèn),盡管避免了軟硬閾值的弊端,,但是其中的參數(shù)在運(yùn)用中取固定值,,因此仍然存在固有偏差和不連續(xù)性。針對(duì)上述問(wèn)題和缺點(diǎn),,文獻(xiàn)[15]提出了一種新閾值函數(shù)改進(jìn)算法,,并將該算法應(yīng)用在指紋圖像處理領(lǐng)域。

該算法在閾值點(diǎn)處連續(xù),,解決了硬閾值函數(shù)帶來(lái)的振蕩問(wèn)題和軟閾值函數(shù)帶來(lái)的偏差問(wèn)題,,可根據(jù)參數(shù)t靈活調(diào)節(jié)閾值以適應(yīng)不同噪聲,但是顯然,,該閾值函數(shù)屬于軟閾值函數(shù)特性,。為了克服軟閾值函數(shù)的缺陷,需要將軟閾值函數(shù)和硬閾值函數(shù)結(jié)合起來(lái)構(gòu)造新閾值函數(shù),故此,,本文在此基礎(chǔ)上結(jié)合文獻(xiàn)[16]進(jìn)一步改進(jìn),,得到如式(9)的改進(jìn)算法,并將該算法首次應(yīng)用在電機(jī)振動(dòng)信號(hào)處理領(lǐng)域,。

當(dāng)u取0~1之間不同值時(shí),,新閾值函數(shù)介于硬閾值函數(shù)和軟閾值函數(shù)之間,這樣不但克服了硬閾值函數(shù)和軟閾值函數(shù)各自存在的缺陷,,同時(shí)通過(guò)調(diào)節(jié)參數(shù)?琢和t使得新閾值函數(shù)相比式(8)變得更靈活,。
下面對(duì)改進(jìn)閾值函數(shù)進(jìn)行分析。
(1)連續(xù)性


綜上所述:新閾值函數(shù)是以?棕′=?棕為漸近線,。
(3)偏差性

(4)閾值可變因子影響分析
當(dāng)α=0,,t→0時(shí),新閾值函數(shù)為軟閾值函數(shù),;t→∞,,新閾值函數(shù)變?yōu)橛查撝岛瘮?shù);α→∞,,新閾值變?yōu)橛查撝岛瘮?shù),。所以,新閾值函數(shù)不僅具有整體連續(xù)性的特點(diǎn),,而且根據(jù)實(shí)際情況進(jìn)行參數(shù)調(diào)節(jié)也十分靈活,。
4 算法驗(yàn)證
若將原始信號(hào)作為標(biāo)準(zhǔn)信號(hào)s(t),則經(jīng)各種降噪模型降噪的估計(jì)信號(hào)![]() 的信噪比(SNR)定義為:
的信噪比(SNR)定義為:

降噪后信號(hào)的信噪比越高,,原始信號(hào)與估計(jì)信號(hào)的均方根誤差越小,,則估計(jì)信號(hào)越接近于真實(shí)信號(hào),降噪效果越好,。
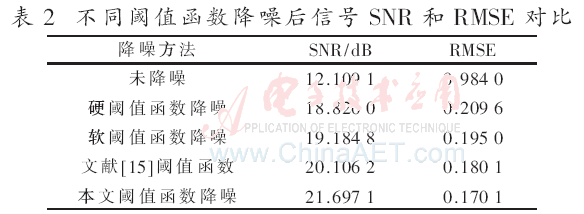
算法驗(yàn)證中首先以MATLAB自帶的信號(hào)為例,,對(duì)其加入一定信噪比(12 dB)的高斯白噪聲,并用固有Heursure,、Sqtwolog,、Minimaxi以及文獻(xiàn)[13]算法和本文新閾值算法分別對(duì)其進(jìn)行降噪處理,,結(jié)果如圖2所示,。用硬閾值函數(shù)、軟閾值函數(shù),、文獻(xiàn)[15]閾值函數(shù)和本文改進(jìn)閾值函數(shù)分別對(duì)其做降噪處理,,結(jié)果如圖3所示。


各種降噪方法性能指標(biāo)如表1,、表2所示,。從表中可以看出,相比于其他方法,改進(jìn)算法的信噪比有所提高,,同時(shí)均方誤差下降,,降噪效果最好,所以該算法優(yōu)于其他算法,。

5 改進(jìn)算法在振動(dòng)信號(hào)降噪中的應(yīng)用
數(shù)據(jù)來(lái)源于遼寧科技大學(xué)國(guó)家大學(xué)科技園電機(jī)振動(dòng)實(shí)驗(yàn)臺(tái)采集的轉(zhuǎn)子不對(duì)中振動(dòng)信號(hào),,采用db4小波函數(shù)。轉(zhuǎn)子的轉(zhuǎn)速為924 r/min,,采樣頻率500 Hz,,采集1 049個(gè)采樣點(diǎn),對(duì)振動(dòng)信號(hào)進(jìn)行5層小波包分解,,采用貝葉斯新閾值,,結(jié)合改進(jìn)閾值函數(shù)對(duì)采樣信號(hào)進(jìn)行降噪處理。
如圖4所示,,轉(zhuǎn)子不對(duì)中故障信號(hào)2倍頻明顯,,同時(shí)在對(duì)應(yīng)尖峰的恢復(fù)上,改進(jìn)閾值函數(shù)結(jié)合新閾值算法降噪效果明顯,。利用該方法進(jìn)行降噪很好地保留了尖峰和突變部分,,并可以將信號(hào)高頻部分和噪聲引起的高頻干擾有效地區(qū)分,對(duì)高頻部分進(jìn)行降噪處理,,提高信噪比,,使沖擊響應(yīng)特性更加突出,便于信號(hào)特征量的提取,。

6 結(jié)論
在電機(jī)振動(dòng)信號(hào)處理過(guò)程中,,振動(dòng)信號(hào)的去噪效果對(duì)電機(jī)振動(dòng)信號(hào)特征提取與分析起著至關(guān)重要的作用。利用貝葉斯新閾值結(jié)合新閾值函數(shù)的新方法,,針對(duì)模擬信號(hào)與實(shí)測(cè)振動(dòng)信號(hào)的降噪處理,,表明在振動(dòng)信號(hào)降噪方面,通過(guò)設(shè)置合適的閾值結(jié)合新閾值函數(shù)能達(dá)到滿意的降噪效果,,既能反映振動(dòng)的真實(shí)特性信息又保留了信號(hào)的高頻部分特性,。本文方法具有一定的使用價(jià)值。
根據(jù)模擬信號(hào)仿真結(jié)果可知,,基于貝葉斯新閾值和改進(jìn)閾值函數(shù)降噪算法都能夠有效地提高信噪比,,降低均方根誤差,同時(shí)抑制高頻噪聲,,能夠恢復(fù)信號(hào)中的真實(shí)有用信號(hào),。通過(guò)實(shí)測(cè)電機(jī)振動(dòng)信號(hào)處理可知,改進(jìn)的降噪算法應(yīng)用在電機(jī)振動(dòng)信號(hào)處理中具有較好的降噪效果,。
參考文獻(xiàn)
[1] 吳光文,,王昌明,,包建東,等.基于自適應(yīng)閾值函數(shù)的小波閾值降噪方法[J].電子與信息學(xué)報(bào),,2014,,36(6):1340-1347.
[2] MALLAT S.A theory for multiresolution signal decomposition:the wavelet representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1989,,11(7):674-693.
[3] DONOHO D L.De-noising by soft-thresholding[J].IEEE Transactions on Information Theory,,1995,41(3):613-627.
[4] 潘泉,,張磊,,孟晉麗,等.小波濾波方法及應(yīng)用[M].北京:清華大學(xué)出版社,,2005.
[5] Grace Chang,,Yu Bin,Martin Vetterli.Adaptive wavelet thresholding for lmage denoising and compression[J].IEEE Trans Image Processing,,2000,,9:1532-1546.
[6] 劉繼紅,賈振紅,,覃錫忠,,等.基于權(quán)重粒子群優(yōu)化閾值的NSCT圖像降噪[J].計(jì)算機(jī)工程,2012,,38(10):209-211.
[7] 陳曉娟,,王文婷,賈明超,,等.基于小波熵自適應(yīng)閾值的語(yǔ)音信號(hào)降噪新方法[J].計(jì)算機(jī)應(yīng)用研究,,2014,31(3):753-755.
[8] 閆峰.基于小波變換語(yǔ)音信號(hào)降噪及DSP算法實(shí)現(xiàn)[D].哈爾濱:哈爾濱工業(yè)大學(xué),,2008.
[9] 謝巍盛,,楊根科.基于尺度噪聲能量估計(jì)的自適應(yīng)語(yǔ)音降噪算法[J].上海交通大學(xué)學(xué)報(bào),2012,,46(9):1146-1150.
[10] DONOHO D L,,JOHNSTONE I M.Wavelet shrinkage:asymp-topia[J].Journal of the Royal Statistical Society,1995,,57(2):301-369.
[11] DAUBECHIES I.The wavelet transform:time-frequency localization and signal analysis[J].IEEE Transactions on Information Theory 2000,,36:961-1005.
[12] 陶新民,徐晶,,杜寶祥,,等.基于小波域廣義高斯分布的軸承故障診斷方法[J].機(jī)械工程學(xué)報(bào),2009,,45(10):61-67.
[13] 敬忠良,肖鋼.圖像融合—理論與應(yīng)用[M].北京:高等教育出版社,2007:26-27.
[14] 李迎春,,孫繼平,,付興建.基于小波變換的紅外圖像降噪[J].激光與紅外,2006,,36(10):988-991.
[15] 黃玉昌,,侯德文.基于改進(jìn)小波閾值函數(shù)的指紋圖像降噪[J].計(jì)算機(jī)工程與應(yīng)用,2014,,50(6):179-181.
[16] 王蓓,,張根耀,李智,,等.基于新閾值函數(shù)的小波閾值降噪算法[J].計(jì)算機(jī)應(yīng)用,,2014,34(5):1499-1502.

