0 引言

　　為了滿足現(xiàn)代無線通信對高速率的要求,，通信系統(tǒng)采用了更加復(fù)雜的調(diào)制方式，對射頻電路設(shè)計的性能指標(biāo)要求也越來越苛刻,。低互調(diào)失真,、高線性度是當(dāng)前無線射頻前端設(shè)計的重要問題之一[1]。射頻功率放大器（PA）處于通信系統(tǒng)中信號發(fā)射機(jī)的末端,，對發(fā)射信號的質(zhì)量起著決定性作用,，然而由于PA工作在大信號下，所以其線性度差一直是難以克服的問題,。常用的PA線性化技術(shù)都是基于系統(tǒng)級的,，電路復(fù)雜、功耗大且價格高,。RF MOS管的非線性特性決定了PA的線性度,，因此，從RF MOS管級對非線性特性進(jìn)行分析和補償,，可以有效提高線性度,，降低功耗和設(shè)計成本，對于集成高線性度的PA和通信系統(tǒng)來說意義重大,。

　　常用的分析非線性電路方法有Taylor級數(shù)法[2],、Volettra級數(shù)法[3]和諧波平衡法。文獻(xiàn)[4]中已經(jīng)使用Taylor級數(shù)和BSIM3模型來研究RF MOS管的非線性特性,。本研究中,，使用了Taylor級數(shù)的分析方法，并基于ADS軟件中的Symbolically Defined Device（SDD）對RF MOS管進(jìn)行非線性特性建模和仿真,，計算出各非線性源對RF MOS管總體非線性度的貢獻(xiàn),，并提出了與之對應(yīng)的線性度提高技術(shù)。

　　本文最后將各種線性提高技術(shù)應(yīng)用在了一款功率放大器上,，該功率放大器采用TSMC 0.18 μm RF CMOS工藝設(shè)計,。仿真結(jié)果表明該功率放大器的線性度提高了4~10 dB，證明了本文對RF MOS管非線性模型分析正確可靠,，提出的線性度提高技術(shù)正確可行,。

1 RF MOS管非線性特性分析

　　根據(jù)通信系統(tǒng)對發(fā)射功率的要求，一般功率放大器工作在大信號區(qū)域,，各種寄生參數(shù)會隨著信號幅度的變化而變化,，即具有很強的非線性特性。圖1（a）是RF MOS管等效電路模型，圖1（b）是其對應(yīng)的非線性等效模型[7],，其中虛線框內(nèi)為MOS管本征參數(shù)模型,，Rg、Rd,、Rs分別表示柵,、漏和源的連接電阻，rds表示輸出電阻,，rsub表示襯底電阻,；Cgd表示柵漏電容，Cgs表示柵源電容,，Cds表示源漏電容,，Cjd表示漏極結(jié)電容；gm為MOS管的跨導(dǎo),。

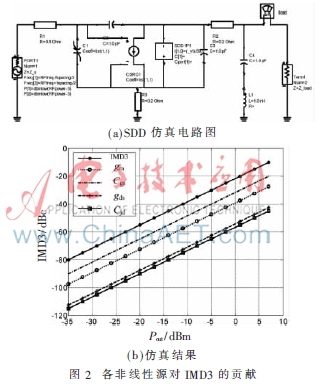
　　由于MOS管的非線性特性,，輸入信號會在輸出端產(chǎn)生互調(diào)失真信號，本文采用IMD3來衡量RF MOS管的線性度,，并利用ADS軟件中的SDD對RF MOS管的IMD3進(jìn)行掃描仿真,，分析出各個非線性源對RF MOS管總體線性度的貢獻(xiàn)。圖2（a）為SDD測試電路圖,，仿真結(jié)果如圖2（b）所示,。從圖2（b）仿真結(jié)果可以看出，柵源電容Cgs,、跨導(dǎo)gm,、輸出導(dǎo)納gds和漏極結(jié)電容Cjd是RF MOS管非線性特性的四個主要來源[5]。

　　使用Taylor級數(shù)的分析方法,，忽略高階系數(shù)和互調(diào)系數(shù),，得到各非線性源的泰勒級數(shù)表達(dá)式為：

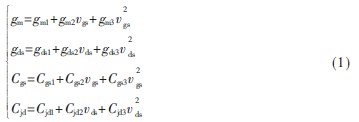
　　在飽和區(qū)，柵漏電容(Cgd)主要是外部電容,，而漏源電容(Cds)接近于零,，所有參數(shù)都可以認(rèn)為是與偏置無關(guān)的。當(dāng)負(fù)載阻抗低時,，gm是最主要的非線性源,，然而，對于一般級別的負(fù)載阻抗,，gds才是最主要的非線性源。在偏置點附近,，Cgs的值會發(fā)生強烈的變化,，即MOS管在大信號狀態(tài)下，從線性區(qū)變化到飽和區(qū)或者從飽和區(qū)變化到線性區(qū)時，Cgs產(chǎn)生很大變化,，從而造成了電路的非線性現(xiàn)象,。寄生電容Cgd幾乎不變，且Cgb的變化也不大,。因此,，當(dāng)選定合適的偏置點使得gm和gds非線性度最小時，此時MOS管的非線性特性幾乎由Cgs來決定[6],。

2 線性度提高技術(shù)

　　2.1 DMGTR技術(shù)

　　由前文的分析可知,，gm的非線性現(xiàn)象主要由于其gm3（跨導(dǎo)的二階倒數(shù)）在零點處，具有對稱的幅值和相反的相位,。因此,，為了提高線性度，采用了一種新型的差分電路gm3消除技術(shù),，即所謂的差分多柵晶體管技術(shù),，簡稱DMGTR[4]。

　　在ADS下對TSMC 0.18 μm RF CMOS工藝下的偽差分NMOS管進(jìn)行g(shù)m3參數(shù)提取,，所選管子尺寸為W/L=35 μm/0.18 μm,。掃描不同差分柵源電壓（范圍：-0.8 V~0.8 V，掃描間隔：0.01 V,，VDD：1.8 V）后,，分別在飽和區(qū)（Vbias=0.65 V）和弱反型區(qū)（Vbias=0.4 V）下得到gm3隨柵源電壓Vgs變化的情況如圖3所示。

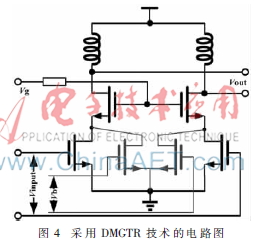
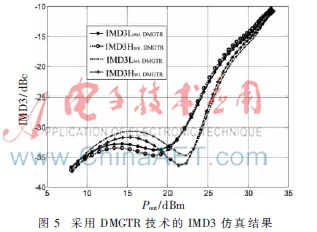
　　由圖3的仿真結(jié)果可以看出,，NMOS管在飽和區(qū)時,，其gm3是負(fù)值，在弱反型區(qū)時,，其gm3是正值,，兩者趨勢相反。實際中,，運放起放大功能時要求功放管處于飽和區(qū),，因此當(dāng)輸入管采用偏置在亞閾值區(qū)的MOS管和偏置在飽和區(qū)的功放管并聯(lián)放大時，利用MOS管在不同偏置條件下gm3的變化趨勢不同,，實現(xiàn)了gm3所產(chǎn)生的非線性度相減,，從而達(dá)到提高RF MOS管線性度的目的，即為DMGTR技術(shù),，其電路原理圖如圖4所示,。在ADS下對采用DMGTR技術(shù)的功率放大器電路進(jìn)行諧波平衡仿真，其IMD3仿真結(jié)果如圖5所示,?？梢钥闯觯捎肈MGTR技術(shù)后，電路的IMD3在一定輸入功率范圍內(nèi)提高了約5 dB,。

　　2.2 PMOS管補償技術(shù)

　　由圖6可以看出,，NMOS的輸入電容隨Vgs增大而增大， PMOS的輸入電容隨Vgs增大而減小,，兩者的變化趨勢是相反的,。仿真采用TSMC 0.18 μm RF CMOS Spice模型，PMOS管和NMOS管的尺寸為W/L=15 360 μm/0.18 μm,，PMOS管偏壓Vpp=1.1 V,。因此，選擇合適的NMOS管和PMOS管的尺寸,，可以使兩者的電容之和保持恒定,，從而提高線性度。補償電路原理圖如圖7所示,。

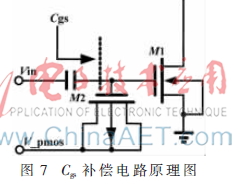
　　在ADS下對采用Cgs補償技術(shù)的功率放大器電路進(jìn)行線性度仿真,，其仿真結(jié)果如圖8所示?？梢钥闯?，采用此補償技術(shù)后，電路的IMD3在一定輸入功率范圍內(nèi)提高了約10 dB,。

　　2.3 其他線性度提高技術(shù)

　　本節(jié)將簡要介紹其中4種常用的技術(shù),，即NMOS管補償技術(shù)、共柵管的柵電容補償技術(shù),、Cjd補償技術(shù)和多級DMGTR技術(shù),。NMOS管的源級通過一個小電阻連接到柵極后，其柵極電容的變化趨勢與NMOS的柵寄生電容也是相反的,。因此,，對此NMOS管的尺寸合理選擇，以及對其偏置做些處理,，該電路也可以用來對Cgs的非線性度進(jìn)行補償,，其原理圖如圖9（a）所示。共柵管柵端的電容也會貢獻(xiàn)相應(yīng)的非線性度,，通過串聯(lián)一個金屬氧化物電容可以減小該點電容的變化,，從而提高線性度，其電路原理圖如圖9（b）,。在高頻下,，Cjd的變化會導(dǎo)致RF MOS管的非線性度。在Cascode結(jié)構(gòu)中,，采用兩個MOS電容接到地可以減小Cjd的變化,，從而提高RF MOS管的線性度,，其電路原理圖如圖9（c）。在DMGTR技術(shù)的基礎(chǔ)上,，在輸入功放管旁邊再并聯(lián)一對NMOS管，相當(dāng)于對gm3進(jìn)行二次補償,，保證gm3在工作范圍內(nèi)為正值,，從而提高線性度，其電路原理圖如圖9（d）,。

3 設(shè)計實現(xiàn)與結(jié)果分析

　　為了驗證上述線性度提高技術(shù)的可行性,，將其分別應(yīng)用在了一款功率放大器上。該功率放大器采用Agilent公司的ADS軟件仿真驗證,，在TSMC 0.18 μm RF CMOS工藝下進(jìn)行設(shè)計,。測量該功率放大器的IMD3，并與采用各個線性度提高技術(shù)后的IMD3進(jìn)行比較,，實驗測試結(jié)果如表1所示,。

　　由表1的結(jié)果可以看出，采用各種線性度提高技術(shù)后,，功率放大器的IMD3提高了4~10 dB,，線性度性能得到改善，證明了本文對RF MOS管非線性模型分析正確可靠以及線性度提高技術(shù)正確可行,。

4 結(jié)論

　　基于ADS軟件對MOS管的線性度進(jìn)行研究,，并對其非線性進(jìn)行技術(shù)補償，提出的DMGTR和PMOS線性化技術(shù)分別對gm和Cgs的非線性進(jìn)行補償,。采用DMGTR技術(shù)后,，電路的IMD3在一定輸入功率范圍內(nèi)提高了接近5 dB；采用PMOS補償技術(shù)后,，電路的IMD3在一定輸入功率范圍內(nèi)提高了接近10 dB,，證明了本文對RF MOS管非線性模型分析正確可靠以及線性度提高技術(shù)正確可行。

　　參考文獻(xiàn)

　　[1] Wei Cheng,，OUDE ALINK M S,，ANNEMA A J，et al.RF circuit linearity optimization using a general weak nonlinea-rity model[J].IEEE Transactions on Circuits and Systems-I：Regular Papers,，2012,，59(10)：2340-2353.

　　[2] TERROVITIS M T,MEYER R G. Intermodulation distortion in current-commutating CMOS mixers[J].IEEE J.Solid-State Circuits，2000,，35(10)：1461-1473.

　　[3] YU W,，SEN S，LEUNG B H.Distortion analysis of MOS track-and-hold sampling mixers using time-varying Volterraseries[J].IEEE Trans.Circuits Syst.II,，1999,，46(2)：101-113.

　　[4] KANG S,，CHOI B，KIM B.Linearity analysis of CMOS for RF application[C].IEEE RFIC Symp.Digest. Monterey：IEEE,，2002：363-366.

　　[5] KANG J,，DAEKYU Y，YOUNGOO Y.Highly linear 0.18 CMOS power amplifier with deep n-well structure[J].IEEE J.Solid-State Circuits,，2006,，41(5)：1073-1080.

　　[6] WANG C，VAIDYANATHAN M,，LARSON L E.A capaci-tance-compensation technique for improved linearity in CMOS classAB power amplifier[J].IEEE J.Solid-State Circuits,，2004，39(11)：1927-1937.

　　[7] KANG J,，JEHYUNG Y,，KYOUNGJOON M，et al.A highly linear and efficient differential CMOS power amplifier with harmonic control[J].IEEE J.Solid-State Circuits,，2006,，41(6)：1314-1322.