摘 要： 針對低功耗電路設(shè)計要求,，基于SMIC 0.18 μm CMOS 工藝,，設(shè)計了一種電流復用兩級共源低噪聲放大器。仿真結(jié)果表明,，在2.4 GHz的工作頻率下,，功率增益為26.26 dB，輸入回波損耗S11為-27.14 dB,輸出回波損耗S22為-16.54 dB,反向隔離度為-40.91 dB,，噪聲系數(shù)為1.52 dB,，在1.5 V的供電電壓下，電路的靜態(tài)功耗為8.6 mW,，并且工作穩(wěn)定,。

　　關(guān)鍵詞： CMOS；電流復用,；阻抗匹配,；低噪聲放大器

0 引言

　　由于具有集成度高、成本低等優(yōu)勢,，當前大多數(shù)無線射頻收發(fā)系統(tǒng)的設(shè)計都采用CMOS技術(shù)[1],。由于低噪聲放大器（LNA）處于接收機前端,，它對整個無線通信系統(tǒng)射頻接收機的性能起著關(guān)鍵性的作用。為了抑制后面各級噪聲對系統(tǒng)的影響,，LNA要求有較好的噪聲性能以及足夠的增益,。為了保證在較大的信號動態(tài)范圍內(nèi)LNA能夠正常工作，要求LNA有足夠的線性度,，同時為了實現(xiàn)最大功率傳輸或最小噪聲系數(shù),，應保證LNA的輸入阻抗與前端源阻抗實現(xiàn)良好的匹配。在實際設(shè)計中,，這些性能指標會相互牽制相互影響,，所以在設(shè)計過程中要對這些性能指標進行折衷處理[2]。

　　本文基于SMIC 0.18 μm CMOS工藝設(shè)計實現(xiàn)了中心頻率為2.4 GHz低噪聲放大器,。文章第1部分分析了電流復用兩級共源LNA的電路結(jié)構(gòu),、輸入阻抗以及最佳MOS管尺寸的選擇,；第2部分是電路仿真結(jié)果并就此結(jié)果進行了詳細的分析,；最后對全文進行總結(jié)。

1 LNA電路設(shè)計與優(yōu)化

　　1.1 電路結(jié)構(gòu)分析

　　為了滿足整個系統(tǒng)的性能要求,，LNA需要足夠的增益,，所以在LNA的設(shè)計中通常采用多級放大器。在多級放大器中,，由于每級電路都要消耗電流,，導致電路電流隨著電路級數(shù)增加而增加。為了降低功耗,，本文采用CS-CS cascaded電流復用結(jié)構(gòu),，電路如圖1所示。LNA的直流偏置電路由M0和R1構(gòu)成,，電源電壓,、電阻R1與M0的柵極和源極電壓決定了M0的工作電流，晶體管M0與M1形成電流鏡,。為了盡可能地減小偏置電路的附加功耗,，M0的柵寬遠小于M1柵寬。為了盡可能地減小偏置電路對交流信號通路的影響,，電阻R2選擇得足夠大,。電感L1、L2和電容Cex實現(xiàn)輸入匹配,，電感L4,、C4、L5和電容C5實現(xiàn)輸出匹配,。在直流時,，電感L3起到短路的作用，此時第二級和第一級共享偏置電流，這樣可以大大降低電路的功耗,。在交流時,，電容C2交流接地，電感L3起到Rfchock作用,，第一級的輸出通過耦合電容C3連接到第二級晶體管M2的柵極,，構(gòu)成兩級共源結(jié)構(gòu)，從而提高了整個電路的功率增益,。

　　1.2 最佳MOS管寬度選擇

　　多級低噪聲放大器的噪聲系數(shù)的表達式為 [3]:

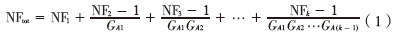
　　公式（1）中,，NFk為第k級的噪聲系數(shù)；GA（k-1）為第k-1級的增益,。由式（1）可知,，NF1和GA1是NFtot取值大小的關(guān)鍵，如果GA1足夠大,，第2級及后面的放大器的噪聲對整體噪聲的影響可以忽略,，因此電路噪聲主要決定于NF1。

　　由經(jīng)典的噪聲理論可推導出MOS管的最小噪聲系數(shù)的表達式為[4]：

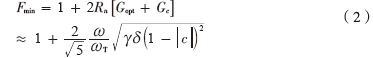
　　其中,，ω為LNA的工作頻率,，ωT為MOS管的截止頻率，γ為漏噪聲系數(shù),，δ為柵噪聲系數(shù),，c為漏噪聲與柵噪聲的相關(guān)系數(shù)。gd0為漏源電壓為0時的漏源跨導,，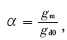

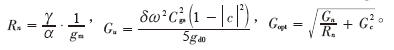
　　公式（2）的最小噪聲系數(shù)是在不考慮功耗的情況下得出的,，考慮到功耗的限制可以得出使噪聲系數(shù)最小的最優(yōu)MOS管的寬度表達式為：

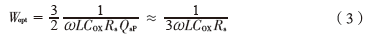
　　若MOS管的寬度取值為Wopt，則可以計算在功耗約束的范圍內(nèi)取得的噪聲系數(shù)為：

　　1.3 輸入匹配電路的優(yōu)化設(shè)計

　　傳統(tǒng)的放大器輸入匹配通常采用源級電感負反饋結(jié)構(gòu)[5-6],，如圖2所示,。

　　由圖2可知，該結(jié)構(gòu)的輸入阻抗為[2]：

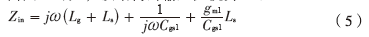
　　在一定的偏置和器件尺寸條件下,，選取適當?shù)腖s使得輸入阻抗為50 ,，即可實現(xiàn)輸入端的阻抗匹配。但是這種結(jié)構(gòu)需要感值很高的柵極電感,，高感值的電感在芯片中會占用很大的面積,，而且在射頻電路設(shè)計中，高感值的電感寄生電阻較大,，對應的噪聲也較大,。

　　本電路的設(shè)計中在晶體管M1的柵源之間并上一個電容Cex,用來調(diào)節(jié)晶體管M1柵源之間電容的大小,進而減小柵極電感的值。此時LNA的輸入阻抗為：

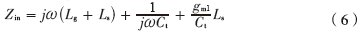
　　其中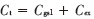

　　輸入電路諧振時,，

　　在LNA處于一定的偏置和器件尺寸的條件下,，通過調(diào)整電感Ls的大小使得輸入阻抗中的實部等于50 ?,，即可實現(xiàn)輸入端的阻抗匹配，而且此時產(chǎn)生的實部不是一個實際的電阻,，因此不用擔心由實際電阻而產(chǎn)生的熱噪聲,，所以不會對放大器的噪聲性能產(chǎn)生影響。通過調(diào)整Lg和Ct的大小使輸入阻抗的虛部的感抗和容抗相互抵消,，使得輸入阻抗的虛部為零,。從式（7）可以看出，在晶體管M1的柵極和源極之間并聯(lián)一個電容Cex后,，所需要的柵極電感的值減小,。

　　1.4 電路穩(wěn)定性分析

　　電路的穩(wěn)定性也是LNA設(shè)計中需要考慮的一個重要的性能指標。在放大器的設(shè)計中,，必須保證放大器的穩(wěn)定性,，否則放大器在一定條件的激勵下有可能會出現(xiàn)自激現(xiàn)象。通常用穩(wěn)定因子K描述一個二端口網(wǎng)絡(luò)的絕對穩(wěn)定條件[7]：

　　其中: 

　　要使得LNA絕對穩(wěn)定,，必須保證K大于1,。

　　2 電路仿真結(jié)果及其分析

　　采用SMIC 0.18 μm CMOS射頻工藝，在Cadence軟件環(huán)境下完成電路各項性能指標的仿真,。工作頻率為2.4 GHz,，在1.5 V工作電壓下,，電路的靜態(tài)功耗為8.6 mW,。

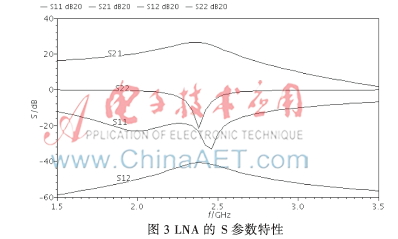
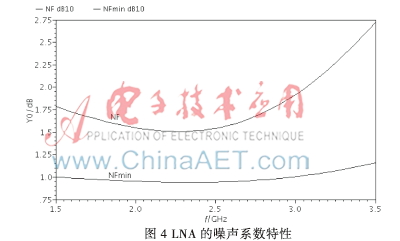
　　電路的S參數(shù)如圖3所示。在中心頻率2.4 GHz處,，正向傳輸增益S21為26.26 dB,，具有足夠的增益，能有效地減小后級電路對噪聲的影響,。輸入反射系數(shù)S11為-27.14 dB,，輸出反射系數(shù)S22為-16.54 dB，說明實現(xiàn)了較好的輸入輸出阻抗匹配,。反向隔離度S12為-40.91 dB,。LNA的噪聲系數(shù)仿真結(jié)果如圖4所示，從圖中可以看出,，在2.4 GHz的工作頻率處,，設(shè)計的低噪聲放大器的噪聲系數(shù)并不等于最小噪聲系數(shù)。若要使電路實現(xiàn)噪聲的完全匹配,，可以通過增加Cex（但會提高電路的最小噪聲系數(shù),降低電路的增益）或增加M1的柵寬 (但會增加功耗)來實現(xiàn),。本文所設(shè)計的LNA在功耗和噪聲系數(shù)之間進行了折衷處理，在較低功耗下實現(xiàn)了較好的噪聲性能,，此時的NF為1.52 dB,。本文對LNA的穩(wěn)定因子Kf也進行了仿真,，仿真結(jié)果如圖5所示。由仿真結(jié)果可以看出Kf始終大于1,，所設(shè)計的低噪聲放大器處于無條件穩(wěn)定,。

3 結(jié)論

　　本文采用電流復用技術(shù)設(shè)計了一個低功耗高增益的低噪聲放大器，通過在輸入級晶體管的柵源之間并上一個電容Cex,減小了柵極電感的值,，降低了芯片的面積,。從電路的仿真可以看出，本文設(shè)計的低噪聲放大器在工作頻率2.4 GHz時具有良好的綜合性能指標,。

　　參考文獻

　　[1] Abidi A A. RF CMOS comes of age [J]. IEEE Journal of Solid-State Circuits , 2004 , 39 (4) : 549-561.

　　[2] Madan A, McPartlin M J, Masse C, et al. A 5 GHz 0.95 dB NF highly linear cascode floating-body LNA in 180 nm SOI CMOS technology [J]. IEEE Microwave and Wireless Components Letters,2012,22(4):200-202.

　　[3] Gray P R, Meyer R G. Analysis and design of analogintegrated circuit( 4th ed)[M]. New York:John Wiley＆Sons, 2001．

　　[4] Lee T H.CMOS射頻集成電路設(shè)計[M]. 余志平,譯. 北京:電子工業(yè)出版社, 2006:258-307.

　　[5] Fujimoto R, Kojima K, Otake S. A 7 GHz 1.8dB NF CMOS low noise amplifier[J]. IEEE Journal of Solid-State Circuits, 2002,37(7):852- 856.

　　[6] Paul L, Johan I, Michiel S. A 0.8 dB NF ESD-protected 9mW CMOS LNA operating at 1.23GHz[J]. IEEE Journal of Solid-State Circuits, 2002,37(6):760-765.

　　[7] Belmas F, Hameau F, Fournier J M. A low power inductorless LNA with double gm enhancement in 130nm CMOS[J].IEEE Journal of Solid-State Circuits,2012,47(5):1094-1103.