摘  要： 螢火蟲算法是一種生物群智能的隨機(jī)優(yōu)化算法，該算法通過模擬螢火蟲在覓食,、擇偶中產(chǎn)生熒光而相互吸引,、移動(dòng)、合作等行為來(lái)解決最優(yōu)化問題,。雖然該算法具有設(shè)置參數(shù)少,、原理簡(jiǎn)單、更新公式清晰等優(yōu)點(diǎn),，但是存在著種群過早收斂到局部最優(yōu)解或者種群收斂速度慢等問題,。為此本文提出蛙跳螢火蟲算法。該算法利用蛙跳的分群思想來(lái)優(yōu)化螢火蟲算法,。利用蛙跳算法對(duì)種群進(jìn)行分群和局部深度優(yōu)化,，不斷地迭代以尋得最優(yōu)解。在對(duì)蛙跳螢火蟲算法研究的基礎(chǔ)上把它應(yīng)用于無(wú)線電頻譜分配中,，獲得比較滿意的頻譜分配方式,。

　　關(guān)鍵詞： 螢火蟲算法；蛙跳算法,；蛙跳螢火蟲算法,；無(wú)線電頻譜

0 引言

　　在當(dāng)今社會(huì)的生產(chǎn)生活中，眾多學(xué)者利用進(jìn)化成功的生物的生活方式來(lái)解決經(jīng)典控制理論及優(yōu)化方法在解決實(shí)際問題時(shí)所出現(xiàn)的瓶頸問題,。其中蟻群優(yōu)化算法利用了螞蟻群體分工協(xié)作的尋徑方式,；隨機(jī)蛙跳算法模擬一群青蛙在覓食過程中分組交換信息再重新分組的過程。這類算法都源于學(xué)習(xí)或模擬某些生物的生存本領(lǐng),，因此此類算法多用于尋優(yōu)或并行處理,，因此又被統(tǒng)稱為群智能優(yōu)化算法。本文將這兩種算法結(jié)合起來(lái)取長(zhǎng)補(bǔ)短,，用于無(wú)線電頻譜分配中,。

1 螢火蟲算法

　　1.1 算法的仿生原理

　　螢火蟲算法是一種仿生群智能優(yōu)化算法，是受螢火蟲個(gè)體的發(fā)光行為啟發(fā)而設(shè)計(jì)的,，最早是由印度學(xué)者Krishnanand[1]等人于2005年提出的GSO（Glowworm Swarm Optimization）,，后來(lái)劍橋大學(xué)的Yang[2]也提出類似的算法,，稱為FA（Firefly Algorithm）。

　　在熱帶和溫帶地區(qū),，夏天的晚上都會(huì)出現(xiàn)數(shù)量巨大的螢火蟲群,，據(jù)統(tǒng)計(jì)自然界中有大概2000種螢火蟲，大多數(shù)都會(huì)發(fā)出短促而有節(jié)奏的閃爍熒光,，有的是為了求偶,，有的是為了捕食或警戒等，科學(xué)家對(duì)此進(jìn)行深入的研究發(fā)現(xiàn)其中的規(guī)律,，構(gòu)造出了螢火蟲算法,。螢火蟲算法是模擬螢火蟲發(fā)光行為構(gòu)造出的一種隨機(jī)優(yōu)化算法，該算法根據(jù)其搜索區(qū)域?qū)ふ姨峁﹤€(gè)體,，向較優(yōu)的螢火蟲移動(dòng),，從而實(shí)現(xiàn)位置優(yōu)化。

　　螢火蟲根據(jù)兩個(gè)因素更新自己的位置,，一是熒光亮度,，二是吸引度[3]。越亮的螢火蟲吸引同伴向其移動(dòng)的概率就越大,，以至于最后都聚集在最亮的螢火蟲周圍,。螢火蟲算法是一種群體智能優(yōu)化算法，通過螢火蟲的種群表示搜索空間中的解,，衡量螢火蟲所處的位置的優(yōu)劣程度（即熒光亮度大?。┯媚繕?biāo)函數(shù)來(lái)表示，將螢火蟲種群優(yōu)勝劣汰過程表示為可行解的替換和變換過程,。

　　1.2 螢火蟲算法的數(shù)學(xué)描述

　　螢火蟲個(gè)體之間相互吸引主要由亮度和吸引度決定,。亮度體現(xiàn)了螢火蟲所處位置的優(yōu)劣，位置又決定了螢火蟲的亮度,，亮度又決定了吸引度,，吸引度進(jìn)而決定了位置移動(dòng)的距離大小和方向。由亮度和吸引度的不斷變化完成目標(biāo)的優(yōu)化過程,。從數(shù)學(xué)的角度描述[4-5]如下：

　?。?）螢火蟲的亮度表達(dá)式

　　式（1）中Ii，j表示螢火蟲i對(duì)螢火蟲j的相對(duì)亮度即吸引度,；Ii表示螢火蟲i在r=0處的熒光亮度,，它與相對(duì)的目標(biāo)函數(shù)相關(guān)，目標(biāo)函數(shù)越優(yōu),，自身亮點(diǎn)越高,；ε表示熒光吸收系數(shù)，表示熒光在傳輸過程中隨著傳輸距離的增加而減少的特性。

　?。?）螢火蟲i被螢火蟲j吸引后的位置移動(dòng)更新函數(shù)

　?。?）螢火蟲的移動(dòng)概率

　　螢火蟲先確定某個(gè)螢火蟲周圍最亮的個(gè)體，這個(gè)更亮的個(gè)體對(duì)這個(gè)螢火蟲的吸引度,，計(jì)算這些吸引度的總和，然后根據(jù)各個(gè)更亮螢火蟲的吸引度占據(jù)總吸引度的比例作為螢火蟲移動(dòng)的概率,，計(jì)算公式如下：

　　其中,，pij表示螢火蟲個(gè)體j向i移動(dòng)的概率，n表示螢火蟲的個(gè)體i周圍比它亮的個(gè)體數(shù)目,。

　　1.3 螢火蟲算法流程

　　算法流程如下：

　?。?）初始化基本參數(shù)：螢火蟲數(shù)目n，光強(qiáng)吸收系數(shù)γ,，步長(zhǎng)因子β,，擾動(dòng)因子α，最大迭代次數(shù)tmax等,。

　?。?）根據(jù)約束條件隨機(jī)初始化螢火蟲個(gè)數(shù)，計(jì)算各個(gè)螢火蟲的目標(biāo)函數(shù)作為螢火蟲自身的亮度,。

　?。?）由式（1）計(jì)算各個(gè)螢火蟲的相對(duì)吸引度，根據(jù)吸引度的大小決定螢火蟲向其他螢火蟲移動(dòng)的概率,。

　?。?）由式（2）計(jì)算各個(gè)螢火蟲的更新位置，最佳位置的螢火蟲進(jìn)行隨機(jī)擾動(dòng),。

　?。?）根據(jù)更新后的位置重新計(jì)算亮度，即適應(yīng)值,。

　?。?）當(dāng)滿足搜索精度或達(dá)到最大的搜索次數(shù)時(shí)轉(zhuǎn)向（7），否則搜索次數(shù)加1,，跳轉(zhuǎn)到（3）,，進(jìn)行下一輪搜索。

　?。?）輸出全局極致個(gè)數(shù)和最優(yōu)個(gè)體值,。

　　算法的時(shí)間復(fù)雜度是O（n2），n為螢火蟲的數(shù)目,。

　　雖然螢火蟲算法有諸多優(yōu)點(diǎn),，如原理簡(jiǎn)單、參數(shù)少、更新清晰,，但與其他群智算法一樣存在過早收斂到局部最優(yōu)解或收斂速度過慢的問題,，為此本文結(jié)合分群的思想進(jìn)行改進(jìn)。

2 隨機(jī)蛙跳算法

　　2.1 算法的仿生學(xué)原理

　　與螢火蟲算法相似,，隨機(jī)蛙跳算法[6]也是一種群智優(yōu)化算法,，最初是為了解決組合優(yōu)化問題，具有高效的計(jì)算性能和優(yōu)良的全局搜索能力,。具體思想是[7]：在一片濕地中生活著一群青蛙,，它們又分為幾個(gè)族群，每個(gè)族群內(nèi)的每個(gè)青蛙進(jìn)行信息共享來(lái)一起尋找食物,，每個(gè)族群在各自尋找食物一段時(shí)間以后所有的族群又聚集在一起,，以達(dá)到共享信息的目的，然后重新分群,，各個(gè)族群又獨(dú)自尋找食物,，通過循環(huán)這個(gè)過程，青蛙共享信息,，盡快找到食物,。該過程既有局部信息的交流，又有全局的信息交流,，算法在執(zhí)行過程中可以有效防止過早陷入局部最優(yōu)解,，向全局最優(yōu)解方向移動(dòng)。

　　2.2 算法的數(shù)學(xué)描述

　?。?）初始蛙跳的群體,，隨機(jī)產(chǎn)生n只青蛙，每只青蛙的位置表示解空間的一個(gè)解,，X=（x1,，x2，…xm）,，x1,，x2，…xm表示解的分量,，m表示解得維數(shù),。

　　（2）根據(jù)實(shí)際情況狀況計(jì)算出每個(gè)青蛙的目標(biāo)值,，對(duì)目標(biāo)值優(yōu)劣進(jìn)行排序,。

　　（3）對(duì)青蛙進(jìn)行分子群,，若分為p個(gè)族群,，每族群有q只青蛙，其中p，q滿足p×q=n,，第1只青蛙分到第1族群,，第2只青蛙分到第2族群，以此類推,，第p只青蛙分到第p族群,，……，第2p只青蛙分到第p個(gè)族群,。依次循環(huán)直到分配完畢,。

　　利用式（4）隨機(jī)從青蛙種群中選取q個(gè)進(jìn)行分組，并將組進(jìn)行排序,，j表示第j只青蛙，pj表示第j只青蛙被選中的概率,。找出最好的族群PB和最差的族群PW,，按式（5）和（6）對(duì)每個(gè)族群進(jìn)行局部深度搜索。

　　上面的公式中rand()產(chǎn)生0~1之間的一個(gè)隨機(jī)數(shù),，Dmax表示青蛙的跳動(dòng)步長(zhǎng),，newpw表示更新后青蛙的位置。如果newpw處于可行解空間,，計(jì)算newpw對(duì)應(yīng)的適應(yīng)值,，如果newpw對(duì)應(yīng)的適應(yīng)值次于oldpw所對(duì)應(yīng)的適應(yīng)值，則采用全集最優(yōu)解PX代替上面公式中的PB更新oldpw,。如果更新之后仍然沒有改進(jìn),，隨機(jī)產(chǎn)生的新的青蛙來(lái)代替PW，重復(fù)上述過程,，直到預(yù)設(shè)的迭代次數(shù)完畢,。所有的族群完成深度搜索后，將所有的族群進(jìn)行混合重新排序,，之后再將青蛙分成子族群,，繼續(xù)全局搜索，直到預(yù)設(shè)的條件滿足為止,。

3 蛙跳螢火蟲算法

　　蛙跳螢火蟲算法[8]就是把螢火蟲算法和隨機(jī)蛙跳算法結(jié)合起來(lái),，具體結(jié)合方式如下：設(shè)置好算法各項(xiàng)參數(shù)：迭代次數(shù)r，族群規(guī)模n,，分群數(shù)目m等,，初始化螢火蟲的族群粒子，根據(jù)目標(biāo)函數(shù)計(jì)算各個(gè)螢火蟲粒子的目標(biāo)值,，按照目標(biāo)值的優(yōu)劣進(jìn)行排序,，按照蛙跳算法進(jìn)行分群。分群之后各個(gè)子種群按照蛙跳算法獨(dú)立進(jìn)行深度優(yōu)化，當(dāng)達(dá)到迭代次數(shù)后又合為一個(gè)種群,，對(duì)總的種群按照螢火蟲算法進(jìn)行尋優(yōu),，達(dá)到迭代次數(shù)后重新分群，重復(fù)以上步驟直到達(dá)到要求或者滿足迭代次數(shù),。

4 利用蛙跳螢火蟲算法對(duì)無(wú)線電頻譜進(jìn)行分配

　　傳統(tǒng)的頻譜管理機(jī)制限定某一頻段內(nèi)的頻譜只有該頻段的授權(quán)用戶可以使用,，造成了這些頻道的頻譜利用率低下且存在大量的頻譜空洞。本文利用蛙跳螢火蟲算法對(duì)這一情況將分配方法進(jìn)行改進(jìn),。

　　4.1 基于蛙跳螢火蟲算法中的基本概念

　?。?）螢火蟲

　　每一種頻譜分配方案只有一只螢火蟲，用矩陣X表示,，X=[x1,，x2，…xn]T,，其中xj是對(duì)信道j的分配向量,，xj=[x1j，x2j,，…xNj],，xij∈{0，1},，xij=1表示第i個(gè)次級(jí)用戶獲得信道j的使用權(quán),，反之失敗。同時(shí)螢火蟲的位置更新,，即每一種方案代表的分配矩陣的元素改變,。

　　（2）熒光亮度

　　每一只螢火蟲所處的位置都會(huì)對(duì)應(yīng)一個(gè)熒光亮度,，即每一種分配方案都能計(jì)算出一個(gè)與之對(duì)應(yīng)的目標(biāo)函數(shù)值,。個(gè)體在當(dāng)前所處的位置的亮度，取決于目標(biāo)函數(shù)值,，目標(biāo)函數(shù)值越高自身亮度越亮,。

　　（3）空間距離rij

　　rij為螢火蟲i與j之間的空間距離,，螢火蟲的位置用坐標(biāo)（x1,，x2，…xN）表示,，其中xj為對(duì)于信道j的分配向量,。公式（1）計(jì)算出螢火蟲i處看到個(gè)體j的亮度。

　　4.2 算法的主要流程

　?。?）輸入螢火蟲算法的各項(xiàng)參數(shù),，輸入無(wú)線分配的參數(shù)等,。

　　（2）初始化螢火蟲粒子,，即各個(gè)頻譜分配方案,，每個(gè)粒子可以按如下的方式初始化：

　　其中，xij表示第i個(gè)次級(jí)用戶獲得信道j的使用權(quán),。

　?。?）對(duì)各個(gè)粒子進(jìn)行評(píng)價(jià)，計(jì)算出目標(biāo)適應(yīng)值,，用蛙跳螢火蟲算法對(duì)種群進(jìn)化尋優(yōu),，達(dá)到迭代次數(shù)后按目標(biāo)適應(yīng)值大小排序，分群,。

　?。?）利用隨機(jī)蛙跳算法對(duì)各個(gè)子種群局部深度優(yōu)化，在尋優(yōu)的過程中如果出現(xiàn)不符合約束的粒子則直接舍去,，重新初始化新粒子代替,，達(dá)到迭代次數(shù)后各種群重新混合。

　?。?）迭代次數(shù)減1，判讀迭代次數(shù)是否為0,，若不為0轉(zhuǎn)到（3）,，否則選出此時(shí)最優(yōu)解，實(shí)驗(yàn)完畢,。

　　4.3 實(shí)驗(yàn)仿真

　　本文利用MATLAB進(jìn)行仿真,，參數(shù)設(shè)置如表1。

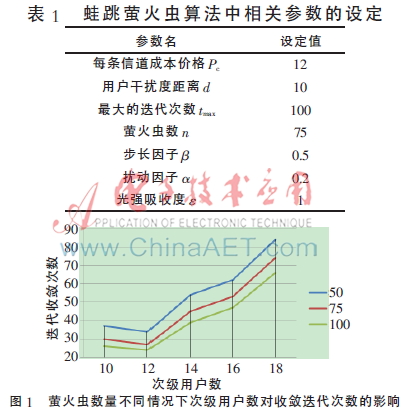
　　系統(tǒng)中參數(shù)的設(shè)定不同會(huì)造成系統(tǒng)性能差異很大,，最大迭代次數(shù)是一個(gè)很重要的參數(shù),，增大tmax可以提高算法精度，但也增加計(jì)算量,，因此選擇合適的tmax至關(guān)重要,。本文中針對(duì)螢火蟲數(shù)量分別在60、80,、100三種情況下,，次級(jí)用戶數(shù)分別是10，12,，14,，16，18時(shí),，測(cè)試收斂的平均迭代次數(shù),，測(cè)試結(jié)果如圖1所示,。從圖中可以看出，螢火蟲的數(shù)量越多收斂速度越快,，并且次級(jí)用戶較少時(shí)收斂速度也快,。除了最大的迭代次數(shù)，種群規(guī)模也就是螢火蟲的數(shù)量n的大小也很重要,。n越大算法精度越高,，計(jì)算量越大，因此選擇一個(gè)合適的種群規(guī)模對(duì)于提高算法整體性能非常重要,。

5 結(jié)論

　　本文主要介紹了螢火蟲算法和隨機(jī)蛙跳算法的基本原理,，并用數(shù)學(xué)方法進(jìn)行描述，對(duì)算法的執(zhí)行流程進(jìn)行了說明,，然后把螢火蟲算法和隨機(jī)蛙跳算法兩者結(jié)合,，形成了蛙跳螢火蟲算法，并且把該算法應(yīng)用于無(wú)線電頻譜分配,。實(shí)驗(yàn)表明,，蛙跳螢火蟲算法在求解組合優(yōu)化問題方面是有效的。

　　參考文獻(xiàn)

　　[1] KRISHNANAND K N,， GHOSE D. Glowworm swarm based optimization algorithm for multimodal functions with collective robotics applications[J]. Multiagent and Grid Systems,， 2006，2（3）：209-222.

　　[2] Yang Xinshe. Firefly algorithms for multimodal optimization [J]. Lecture Note in Computer Sciences,， 2010（3）：169-178.

　　[3] KWIECIEN J,， FILIPOWICZ B. Firefly algorithm in optimization of queueing system[J]. Bulletin of the Polish Academy of Sciences. Technical Sciences， 2012,，60（2）：363-368.

　　[4] GANDOMi A H,， Yang Xinshe， ALAVI A H. Mixed variable structural optimization using firefly algorithm[J]. Computers & Structures,， 2011,， 89（ 23-24）：2325-36.

　　[5] 莫愿斌，劉付永,，馬彥追.模擬生物理想自由分布模型的螢火蟲算法[J].計(jì)算機(jī)與應(yīng)用化學(xué),，2014，31（2）：153-160.

　　[6] HENSHALL P,， PALMER P. A leapfrog algorithm for coupled conductive and radiative transient heat transfer in participating media[J]. International  Journal of  Thermal Sciences,， 2008，47（4）：388-398.

　　[7] 宋曉華,，楊尚東,，劉達(dá).基于蛙跳算法的改進(jìn)支持向量機(jī)預(yù)測(cè)方法及應(yīng)用[J].中南大學(xué)學(xué)報(bào)（自然科學(xué)版），2011,，42（9）：2737-2740.

　　[8] 李洋.蛙跳螢火蟲算法及其在含風(fēng)電場(chǎng)的電力系統(tǒng)調(diào)度中的應(yīng)用[D].上海：華東理工大學(xué),，2013.