摘 要: 針對(duì)微波加熱物料難以建立準(zhǔn)確模型的問(wèn)題,采用粒子群算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)后,對(duì)微波加熱物料的溫度變化構(gòu)建系統(tǒng)模型。在該模型上,對(duì)溫度的變化趨勢(shì)進(jìn)行預(yù)測(cè)。實(shí)驗(yàn)結(jié)果表明,經(jīng)過(guò)粒子群算法優(yōu)化后的BP網(wǎng)絡(luò),具有更高的精度,預(yù)測(cè)能力顯著提高。
關(guān)鍵詞: BP神經(jīng)網(wǎng)絡(luò);粒子群優(yōu)化算法; 微波加熱;溫度預(yù)測(cè)
0 引言
微波作為一種新型能源在工業(yè)上開始得到廣泛應(yīng)用。微波加熱的原理與常規(guī)加熱不同,常規(guī)加熱是利用熱傳導(dǎo)的原理加熱。而微波加熱是利用外加電場(chǎng),改變介質(zhì)分子間的運(yùn)動(dòng)情況并使分子間相互摩擦產(chǎn)生熱量,因此,加熱效果是由里及表。與傳統(tǒng)加熱相比,微波加熱具有提取時(shí)間短、溫度低、耗能低、品質(zhì)高等優(yōu)良特性[1]。由于微波加熱速度快,普通的反饋控制方法有嚴(yán)重的時(shí)間滯后問(wèn)題,媒質(zhì)內(nèi)部出現(xiàn)熱點(diǎn),出現(xiàn)熱失控,可能燒毀工業(yè)物料,甚至引發(fā)爆炸,因此存在較大的安全隱患[2]。
解決智能實(shí)時(shí)控制微波加熱的一個(gè)關(guān)鍵問(wèn)題就是溫度控制。輸出功率要伴隨負(fù)載溫度的變化而改變輸出值,因此需要實(shí)時(shí)監(jiān)測(cè)負(fù)載的溫度值。由于大功率微波加熱存在嚴(yán)重的時(shí)間滯后問(wèn)題,因此,溫度預(yù)測(cè)就成了解決問(wèn)題的關(guān)鍵所在。常見的溫度預(yù)測(cè)方法有:人工神經(jīng)網(wǎng)絡(luò)、時(shí)間序列、支持向量機(jī)等[3]。本文采用粒子群算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的方法進(jìn)行了加熱物料溫度變化趨勢(shì)的預(yù)測(cè),實(shí)驗(yàn)仿真結(jié)果證實(shí)了該方法的有效性。
1 PSO-BP神經(jīng)網(wǎng)絡(luò)在微波加熱中的具體應(yīng)用
1.1 粒子群算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)
BP神經(jīng)網(wǎng)絡(luò)是一種3層或者3層以上的神經(jīng)網(wǎng)絡(luò),包括輸入層、輸出層和隱含層。它的訓(xùn)練算法包括正向和反向傳遞兩個(gè)過(guò)程。輸入信息通過(guò)隱含層傳遞給輸出層,將輸出信號(hào)和預(yù)測(cè)信號(hào)做比較,若有誤差,則采用誤差反向傳播方法,將誤差信息沿原網(wǎng)絡(luò)返回,從輸出層經(jīng)過(guò)中間各層逐層向前修正網(wǎng)絡(luò)的連接權(quán)值[4]。隨著不斷學(xué)習(xí),誤差將越來(lái)越小,最終使誤差到達(dá)指定的精度。但是BP網(wǎng)絡(luò)主要由經(jīng)驗(yàn)和反復(fù)試驗(yàn)確定參數(shù),算法訓(xùn)練時(shí)間較長(zhǎng),效率不高,造成網(wǎng)絡(luò)性能低下。
粒子群算法(PSO)將每個(gè)個(gè)體抽象成優(yōu)化問(wèn)題的可能解,再根據(jù)需要優(yōu)化的目標(biāo)函數(shù)確定一個(gè)具體值,再用一個(gè)速度來(lái)決定它們的方向和距離,粒子通過(guò)自己和其他粒子的飛行經(jīng)驗(yàn)來(lái)動(dòng)態(tài)調(diào)整,并追尋當(dāng)前最優(yōu)粒子,不斷迭代以找到最優(yōu)解[5]。其算法公式為:
vid=vid+c1·rand()·(pid-xid)+c2·rand()·(pgd-xid)(1)
本文研究的對(duì)象是微波加熱物料的溫度,因此輸出量是要預(yù)測(cè)的未來(lái)時(shí)刻物料的溫度,溫度預(yù)測(cè)模型設(shè)計(jì)為3層BP神經(jīng)網(wǎng)絡(luò)。輸入層擬定為加熱時(shí)間和介質(zhì)的反射功率,輸出層為預(yù)測(cè)的溫度[6]。隱含層個(gè)數(shù)的確定至今為止沒(méi)有明確的結(jié)論,只能根據(jù)特定的問(wèn)題,結(jié)合經(jīng)驗(yàn)公式[7]給出估計(jì)值。這里采用的經(jīng)驗(yàn)公式為:

其中,m和n分別表示輸入層和隱含層的神經(jīng)元個(gè)數(shù),a是[0,10]之間的常數(shù)。因此,本文擬定隱含層神經(jīng)元個(gè)數(shù)為3~15,根據(jù)試錯(cuò)法,當(dāng)MSE的結(jié)果達(dá)到最小時(shí),確定隱含層神經(jīng)元的個(gè)數(shù)[8]。
輸入層和隱含層的傳遞函數(shù)分別選定為tansig和purelin,訓(xùn)練函數(shù)采用trainlm。根據(jù)每秒采集到的數(shù)據(jù),整理并訓(xùn)練樣本。
BP神經(jīng)網(wǎng)絡(luò)設(shè)置參數(shù)為:
最大訓(xùn)練次數(shù):net.trainParam.epochs=100;
訓(xùn)練目標(biāo):net.trainParam.goal=0.000 4;
學(xué)習(xí)率:net.trainParam.lr=0.1。
粒子群算法設(shè)置參數(shù)為:
加速常數(shù):c1=c2=1.49
進(jìn)化次數(shù):maxgen=100
種群規(guī)模:sizepop=30
粒子位置和速度取值區(qū)間分別為[-5,5]和[-1,1]。
設(shè)置取優(yōu)化后的權(quán)值、閾值訓(xùn)練網(wǎng)絡(luò)[9]。
1.2 實(shí)驗(yàn)設(shè)備及過(guò)程
在本文中,以工業(yè)加熱煤作為實(shí)驗(yàn)。其中磁控管微波功率源為控制對(duì)象,被控物理量為溫度參數(shù)。該實(shí)驗(yàn)裝置主要由以下幾部分組成:磁控管微波功率輸入控制系統(tǒng)、傳送帶、傳感測(cè)溫器、溫度檢測(cè)裝置等,裝置如圖1所示。在工業(yè)煤加熱過(guò)程中,對(duì)煤從初始溫度加熱到擬定的上限溫度150℃。在系統(tǒng)加熱過(guò)程中,每間隔30 s對(duì)煤炭進(jìn)行溫度采集并記錄,同時(shí)記錄該時(shí)刻的輸入功率和反射功率值。

2 實(shí)驗(yàn)結(jié)果及分析
2.1 BP模型預(yù)測(cè)
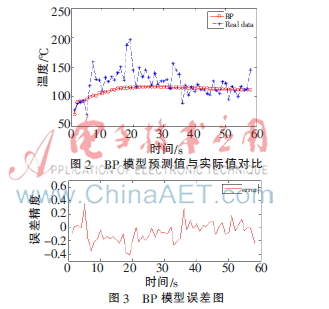
在BP模型預(yù)測(cè)中,預(yù)測(cè)值與實(shí)際值對(duì)比如圖2所示,誤差分析如圖3所示。
2.2 PSO-BP模型預(yù)測(cè)

在PSO-BP模型預(yù)測(cè)中,預(yù)測(cè)值與實(shí)際值如圖4所示,誤差分析如圖5所示。
2.3 結(jié)果分析
(1)BP和PSO-BP兩個(gè)模型的預(yù)測(cè)值都比較趨近實(shí)際值,但部分點(diǎn)誤差較大,原因如下:①在工業(yè)中,受外界干擾的情況較多;②采集時(shí)間間隔比較長(zhǎng),因此溫度的漲幅相對(duì)較大;③由于加熱對(duì)象煤是固體,因此存在熱失控的點(diǎn),但這些采集的特殊點(diǎn)的溫度不能代表煤整體的溫度,所以導(dǎo)致有些點(diǎn)誤差較大。此時(shí),預(yù)測(cè)值比測(cè)量值更能反映煤整體的真實(shí)溫度。
(2)從預(yù)測(cè)的精度分析,PSO-BP預(yù)測(cè)的精度比純BP要高。
綜上,PSO-BP神經(jīng)網(wǎng)絡(luò)的模擬結(jié)果比BP神經(jīng)網(wǎng)絡(luò)更接近測(cè)量數(shù)據(jù),精度更高,訓(xùn)練所需時(shí)間更少。
3 結(jié)論
本文針對(duì)微波加熱物料系統(tǒng)具有時(shí)變性、滯后性和非線性的特性,建立神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型。實(shí)驗(yàn)仿真結(jié)果表明,使用粒子群算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)進(jìn)行溫度預(yù)測(cè),能夠達(dá)到最優(yōu)的擬合效果,并提高了預(yù)測(cè)的速度和精度。這將為下一步的生產(chǎn)實(shí)踐提供理論指導(dǎo),為工業(yè)生產(chǎn)提供新的技術(shù)支持。
參考文獻(xiàn)
[1] 張?zhí)扃瞢I(xiàn)奎,張兆鏜.微波加熱原理、特性和技術(shù)優(yōu)勢(shì)[J].筑路機(jī)械與施工機(jī)械化,2008,25(7):10-14.
[2] 劉長(zhǎng)軍,申?yáng)|雨.微波加熱陶瓷中熱失控現(xiàn)象的分析與控制[J].中國(guó)科學(xué),2008,38(7):1097-1105.
[3] 汪建宇,羅祥遠(yuǎn).微波加熱自動(dòng)控制系統(tǒng)[J].微計(jì)算機(jī)信息,2003,19(10):16-17.
[4] 王龍剛.基于PSO-BP的智能溫度控制器[D].西安:西安科技大學(xué),2012.
[5] 黃文秀.粒子群優(yōu)化算法的發(fā)展研究[J].軟件,2014(4):73-77.
[6] 王龍剛,侯媛彬.BP-PSO在電加熱爐中的溫度智能預(yù)測(cè)[J].自動(dòng)化儀表,2013,34(1):54-56.
[7] 李松,劉力軍,翟曼.改進(jìn)粒子群算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的短時(shí)交通流預(yù)測(cè)[J].系統(tǒng)工程理論與實(shí)踐,2012,32(9):2045-2049.
[8] 張俊,沈軼.神經(jīng)網(wǎng)絡(luò)指數(shù)穩(wěn)定性分析的一種方法[J].華中科技大學(xué)學(xué)報(bào)(自然科學(xué)版),2003,31(1):7-9.
[9] 胡冰蕾.基于遺傳優(yōu)化的BP神經(jīng)網(wǎng)絡(luò)算法的短期負(fù)荷預(yù)測(cè)[J].供用電,2010,27(6):42-44.

