摘  要： 在片上系統(tǒng)高速發(fā)展的今天,，尋求高性能低功耗的設(shè)計(jì)架構(gòu)是目前的最大需求,。為了滿足對架構(gòu)愈發(fā)嚴(yán)格的要求，提出一套簡單有效的片上系統(tǒng)優(yōu)化方法,。該方法通過優(yōu)化算法將關(guān)聯(lián)性強(qiáng)的設(shè)備放置在同一條總線上來降低轉(zhuǎn)接橋的通信量,，進(jìn)而減小整個系統(tǒng)的延遲，得到高性能SoC架構(gòu),。為驗(yàn)證該方法的可行性,，最后建立一個SoC系統(tǒng)進(jìn)行驗(yàn)證。該SoC系統(tǒng)經(jīng)過優(yōu)化后,，系統(tǒng)事件傳輸?shù)难舆t時間明顯減少,。

　　關(guān)鍵詞： 片上系統(tǒng)；系統(tǒng)優(yōu)化,；子集最優(yōu),；通信模型

0 引言

　　隨著片上系統(tǒng)System-on-Chip（SoC）的發(fā)展，業(yè)界開始追求在性能,、功耗,、成本三者之間的最佳平衡點(diǎn),。高性能SoC已成為IC界的焦點(diǎn)。

　　針對該問題,，PINTO A等人對設(shè)備的接口和相應(yīng)總線布局布線進(jìn)行重新設(shè)計(jì),，使得系統(tǒng)的通信不同于之前的點(diǎn)對點(diǎn)通信方式[1]。PANDEY S等人則致力于找到相對高效的總線位寬與總線數(shù)目[2-3],，其方法是在綜合時對總線上設(shè)備接口的緩沖寬度與深度進(jìn)行權(quán)衡,，進(jìn)而提出一種時間離散的馬爾科夫鏈。

　　在集成電路設(shè)計(jì)的系統(tǒng)架構(gòu)研究主要從軟件調(diào)度和硬件拓?fù)鋬蓚€方面進(jìn)行,。其中,，軟件調(diào)度主要是通過對處理器指令調(diào)度的重新規(guī)劃來提升各個處理器之間的通信流程。如Wang Yi重新安排事件調(diào)度[4],。參考文獻(xiàn)[5]選用的是多層總線的模式。這個方向的研究還有在網(wǎng)格環(huán)境下[6]與群組架構(gòu)下的[7],。

　　本文針對目前硬件拓?fù)浞椒▽?shí)現(xiàn)復(fù)雜的問題,，提出一套簡單有效的優(yōu)化辦法，將側(cè)重點(diǎn)放在系統(tǒng)總線之間設(shè)備的關(guān)聯(lián)性上,，通過優(yōu)化算法將關(guān)聯(lián)性強(qiáng)的設(shè)備放置在同一條總線上來降低轉(zhuǎn)接橋的通信量,，進(jìn)而減小整個系統(tǒng)延遲。

1 系統(tǒng)建模

　　在系統(tǒng)模型中,，每個設(shè)備作為一個頂點(diǎn),，設(shè)備之間的任務(wù)量用對應(yīng)的權(quán)重值表示。該權(quán)重值代表兩個設(shè)備之間的通信量,。若任意兩個設(shè)備Ci和Cj之間存在通信則通過相應(yīng)的有向線段來表示,，如（Ci，Cj）對應(yīng)的權(quán)重值Weight（見式（1））,，表示在事件傳輸過程中由設(shè)備Ci向Cj設(shè)備總共發(fā)送大小為Weight數(shù)據(jù)量,。

　　Weight=Avg.size×trans.num（1）

　　2 系統(tǒng)優(yōu)化

　　2.1 系統(tǒng)通信量定義

　　首先，假設(shè)設(shè)備總數(shù)為偶數(shù),。即設(shè)備集合S總共有2n個元素,，則設(shè)備之間的通信矩陣為C=｛cij｝，i,，j=1,，…，2n且cii為0,。i和j在這里分別代表著系統(tǒng)中任意兩個設(shè)備,。cij表示（Ci，Cj）和（Cj,，Ci）的權(quán)重和,，且cij為非負(fù)值,，于是可以看出矩陣C為對稱矩陣。

　　從而降低T的值,，也就降低轉(zhuǎn)接橋需要承載的通信量,。假設(shè)存在子集X和Y，XA,，YB且|X|=|Y|≤n/2,，所以該算法重點(diǎn)是從A和B集合中分別確定要交換的X和Y的子集。

　　假設(shè)a∈A,，則a與A集合的通信量定義為內(nèi)部通信量Ia,，a與B集合的通信量定義為外部通信量Ea，則：

　　同樣地,，假設(shè)存在b∈B,，則外部通信量與內(nèi)部通信量之差Dz=Ez-Iz，其中z∈S,。并且假設(shè)t為整個集合S中除去與a和b有關(guān)的外部通信量總和,，則整個系統(tǒng)的外部通信量如式（5）所示。

　　T=t+Ea+Eb-Cab（5）

　　當(dāng)a和b互換之后,，整個系統(tǒng)的外部通信量為T′,，如式（6）所示。

　　T′=t+Ia+Ib+Cab（6）

　　于是a和b互換之后系統(tǒng)的外部通信量的下降為：

　　decline=T-T′=Da+Db-2Cab（7）

　　2.2 系統(tǒng)算法優(yōu)化

　　通過下面的步驟對系統(tǒng)進(jìn)行優(yōu)化,。

　?。?）先計(jì)算S集合中的每個元素的D值；

　?。?）選取ai∈A,，bj∈B，使得相應(yīng)的g1為最大值,；

　?。?）假設(shè)在步驟（2）得到一對最大值對應(yīng)為a1′和b1′，接下來計(jì)算除去這兩個元素剩下元素的D值,，即范圍分別變?yōu)锳-{a1′}和B-{b1′},。此時的D值可以通過下面的兩式來計(jì)算：

注意到有一部分gi<0。則將X和Y兩個子集交換后整個系統(tǒng)外部通信量降低了gi=G,。于是在這里需要確定k值來確保gi=G為最大值,。注意到，當(dāng)gk+1≤0時便找到G的最大值所對應(yīng)的k值,，若滿足k>0就表示交換X和Y兩個子集就會使得外部通信量降為最低,，同時也表明該轉(zhuǎn)接橋的通信量已經(jīng)達(dá)到局部最大優(yōu)化值。

　　以X和Y兩個子集交換之后重新組合的A′或B′集合為準(zhǔn),，在其內(nèi)部進(jìn)行子集劃分,，繼續(xù)從步驟（1）開始新的循環(huán),，直到優(yōu)化完系統(tǒng)的每個轉(zhuǎn)接橋。

　　特殊情況可以適當(dāng)?shù)匮a(bǔ)充空元素z,，即z元素的Iz=0且Ez=0,。補(bǔ)充完之后繼續(xù)使用前面算法對元素的分布進(jìn)行優(yōu)化。

3 實(shí)驗(yàn)實(shí)例

　　為證明算法的可行性,，以圖1所示系統(tǒng)為例,。如圖1（a）所示，有a,、b,、c、d,、e總共5個設(shè)備,，參考第1節(jié)的建模。其系統(tǒng)對應(yīng)的通信矩陣如式（11）所示,。

　　C= 0 10 5 20 3510 0 5 0 0 5 5 0 0 2520 0 0 0 535 0 25 5 0（11）

　　設(shè)備優(yōu)化前的排布如圖1（a）所示,，最優(yōu)排列如圖1（b）所示。

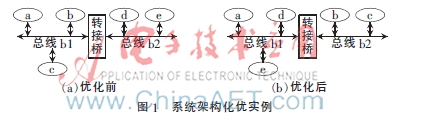
　　在第二節(jié)中提到過,，轉(zhuǎn)接橋傳遞的事件權(quán)重越小，則代表通過轉(zhuǎn)接橋的數(shù)據(jù)總量就越小,，相應(yīng)地整個系統(tǒng)的事件傳輸?shù)难舆t時間也就越少,。

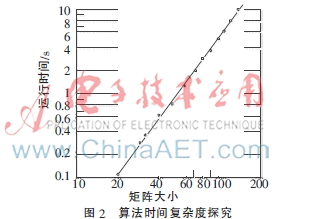
　　但是當(dāng)設(shè)備的個數(shù)增加時，窮舉算法的時間復(fù)雜度呈指數(shù)方式增長,，所以窮舉算法不可取,。然而采用該算法的時間復(fù)雜度為n2logn，并且隨著設(shè)備數(shù)的增長,，算法的運(yùn)行時間如圖2所示,。由此可見該算法具有靈活高效性。

4 結(jié)論

　　越來越多的實(shí)踐和研究表明,，SoC系統(tǒng)級設(shè)計(jì)在整個SoC設(shè)計(jì)中占有非常重要的地位,。本文在著力于解決SoC架構(gòu)的優(yōu)化問題，通過對系統(tǒng)問題規(guī)范的模型化,，提出一種架構(gòu)優(yōu)化的方法,。該方法通過動態(tài)分析可以優(yōu)化SoC的系統(tǒng)設(shè)計(jì)，并且方法靈活,，不拘于軟件,，實(shí)施起來相對簡單。為驗(yàn)證算法的可行性,，本文設(shè)置了5個模塊組成的總線系統(tǒng),，實(shí)驗(yàn)結(jié)果證實(shí)該算法可以快速有效地減小系統(tǒng)通信的延遲周期,，得到高性能SoC架構(gòu)。

參考文獻(xiàn)

　　[1] PINTO A,， CARLONI L P,， SANGIOVANNI-VINCENTELLI A L. A methodology for constraint-driven synthesis of on-chip communications[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems， 2009,， 28（3）：364 -377.

　　[2] PANDEY S,， GLESNER M， MUHLHAUSER M. On-chip communication topology synthesis for shared multi-bus based architecture[C]. 2005 International Conference on Field Programmable Logic and Applications,， IEEE,， 2005：374-379.

　　[3] PANDEY S， ZIMMER H,， GLESNER M,， et al. High level hardware/software communication estimation in shared memory architecture[C]. IEEE International Symposium on Circuits and Systems， ISCAS 2005,， IEEE,，2005，1：37-40.

　　[4] Wang Yi,， Liu Duo,， Qin Zhiwei， et al. Optimally removing intercore communication overhead for streaming applications on MPSoCs[J]. IEEE Transactions on Computers,， 2013,， 62（2）：336-350.

　　[5] HSIU P， HSIEH C,， LEE D,， et al. Multilayer bus optimization for real-time embedded systems[J]. IEEE Transactions on Computers， 2012,，61（11）：1638-1650.

　　[6] Zhu Qian,， AGRAWAL G. Resource allocation for distributed streaming applications[C]. ICPP ′08. 37th International Conference on Parallel Processing， IEEE,， 2008：414-421.

　　[7] Qun Xu C,， Xue C J， Hu B C,， et al. Computation and data transfer co-scheduling for interconnection bus minimization[C]. Design Automation Conference,， ASP-DAC 2009. Asia and South Pacific， IEEE,， 2009：311-316.