摘  要： 針對室內(nèi)聲學非線性系統(tǒng)室內(nèi)沖激響應快速檢測的問題,，提出了一種基于連續(xù)指數(shù)正弦掃頻信號綜合檢測的方法。通過簡要介紹非線性系統(tǒng)Volterra模型后,，著重闡述了作為激勵信號的連續(xù)指數(shù)正弦掃頻信號和實現(xiàn)非線性系統(tǒng)沖激響應快速檢測的基本原理和相關技術,。最后，通過一個應用實例驗證了該方法的可行性和快速性,。

　　關鍵詞： 非線性系統(tǒng),；沖激響應；連續(xù)指數(shù)掃頻信號；快速檢測

0 引言

　　在傳統(tǒng)的室內(nèi)聲學沖激響應測量中,，一般采用周期性脈沖[1]和最大長度序列[1-2]兩種檢測方法,。然而，周期性脈沖測量不但測試時間長,、信噪比差,，而且由于激勵能量低而不能輸出非線性失真；而最大長度序列測量雖然改善了其信噪比,，然而,，其要求系統(tǒng)必須有良好的線性。因此,，傳統(tǒng)的方法無法分離非線性系統(tǒng)的線性與非線性響應,，基于以上的問題，本文提出了一種基于非線性系統(tǒng)的Volterra數(shù)學模型,，采用連續(xù)指數(shù)正弦掃頻信號作為激勵信號,，利用Hilbert-Huang變換技術和相關的逆濾波器技術實現(xiàn)快速簡捷的解決方法。

1 非線性系統(tǒng)的數(shù)學模型

　　室內(nèi)聲學系統(tǒng)一般可認為信號先經(jīng)過一個非線性系統(tǒng),，然后再在一個線性系統(tǒng)中傳輸,，其原理框圖如圖1所示。

　　對于一個無記憶的非線性系統(tǒng)的特征可由N階Volterra核函數(shù)[3]KN（t）表示,，非線性的系統(tǒng)響應如式（1）所示：

　　Farina[4-5]指出該模型下的非線性系統(tǒng)的全局響應可以由一個高斯白噪聲n（t）加上一系列的沖激響應hi（t）（hi（t）=ki（t）?茚h（t））和相應不同功率的輸入信號做卷積的結果組成,。該模型下的全局響應如式（2）所示：

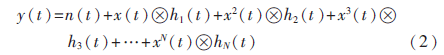
　　在實際應用中，這樣的系統(tǒng)不失一般性,。然而,，實踐中測量這種系統(tǒng)的各階沖激響應函數(shù)hi（t）往往又是非常耗時、困難和復雜的,。下面將介紹一種通過采用特定的激勵信號測量和相關的技術處理,，快速獲取系統(tǒng)各階沖激響應分布的方法。

2 系統(tǒng)信號源的選擇和沖激響應實現(xiàn)的相關技術

　　2.1 激勵信號的選擇

　　在測量方法中,，既希望測量較寬的頻帶,，又希望測量時間盡可能短，并且還希望在測量的頻率范圍內(nèi)得到更為精確的結果,。在傳統(tǒng)的測量中,，主要選擇線性正弦掃頻信號和離散指數(shù)掃頻信號兩種信號作為激勵信號,。線性正弦掃頻信號作為激勵信號,，其頻率呈線性連續(xù)變化，在22 Hz~22 kHz的頻率范圍下測試,，測試時間大概需要15 s,；為縮短測量時間，S.Temme等[6]提出了離散指數(shù)掃頻信號，該信號頻率點以指數(shù)比率增長,，該信號是以犧牲測量精度為代價,，換取更短的測量時間，但是,，在精度為1/24倍頻程下測試,，測量時間也需要十多秒。

　　為了解決以上兩種信號在時間和精度上的問題,，本文采用連續(xù)指數(shù)正弦掃頻信號作為激勵信號,。該激勵信號的形式如式（3）所示：

　　其中，A為信號的幅度,，（t）為信號的瞬時相位,，T為信號掃頻的總時間，w1和w2分別為信號的起始頻率和終止頻率,。

　　該激勵信號隨著時間的變化,，其頻率呈指數(shù)連續(xù)增長，在1 s內(nèi)從起始頻率20 Hz到終止頻率20 kHz的測量結果如圖2所示,。

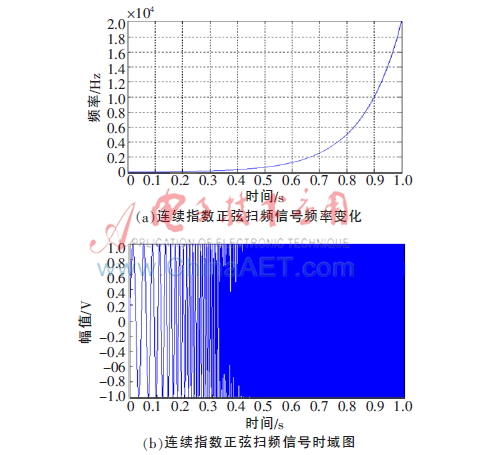
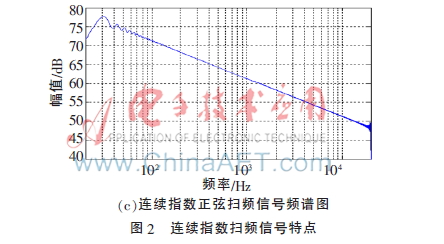
　　由圖2（a）可知,，該激勵信號能在較短時間內(nèi)連續(xù)測試頻率點，因此,，得到的測量頻率更精確,。結合圖2（b）和（c）可知，激勵信號隨著頻率的增加,，能量降低,。如圖2（c）所示，激勵信號的頻譜是一個粉紅譜,，下文將介紹根據(jù)這樣的一個頻譜進行的幅度調(diào)制,。另外，該激勵信號還有一個重要的特點,，如下式（4）所示,。

　　由上式可知，激勵信號某時刻頻率的N倍,，等于該激勵信號頻率延時?駐t對應的頻率,，即?駐t表示了N次諧波出現(xiàn)的時刻與基波之間的時間間隔。此時間間隔只與激勵信號的起始頻率,、終止頻率,、掃頻總時間和N有關。因此,，由式（5）可以確定某時刻頻率的N次諧波出現(xiàn)的時刻,。

　　2.2 沖激響應實現(xiàn)的基本原理

　　為了能夠?qū)崿F(xiàn)快速檢測系統(tǒng)各階沖激響應,，需要構造一個逆濾波器x′（t），它應滿足與激勵信號相卷積后,，其結果為狄拉克函數(shù)δ（t）,。再結合第1節(jié)非線性系統(tǒng)的描述，在連續(xù)指數(shù)正弦掃頻激勵下,，非線性系統(tǒng)的沖激響應函數(shù)形式如式（6）所示：

　　其中,，hi（t）表示第i階的沖激響應，?駐ti表示第i階的沖激響應與第1階沖激響應（即線性響應）之間的時間間隔,，即上節(jié)介紹中的?駐t,。由式（6）可知，由于連續(xù)指數(shù)掃頻信號和特定的逆濾波器的引入,，一個復雜的非線性系統(tǒng)的線性沖激響應和各階非線性沖激響應以?駐ti的時間間隔被分開,。另外，從某種意義上來說這一特定的逆濾波器也是后續(xù)系統(tǒng)另一種形式上的激勵信號,，下一節(jié)將介紹這一特定的逆濾波器,。

　　2.3 沖激響應實現(xiàn)的相關技術——逆濾波器的實現(xiàn)

　　由上節(jié)可知，逆濾波器的創(chuàng)建基于非線性失真響應和激勵信號,。另外,，考慮實際測量中，信號總是因果的,，因此,，還要求逆濾波器應是一個因果的、穩(wěn)定的信號,。根據(jù)參考文獻[7]中對創(chuàng)建逆濾波器的各種技術的分析,，采用最簡單的最小二乘法技術求解逆濾波器。建立最小二乘法方程如式（7）所示：

　　[R]·{g}={k}（7）

　　其中,，[R]矩陣為托普利茲矩陣,，{g}為逆濾波器方程向量，{k}為系統(tǒng)響應函數(shù)方程向量,。

　　另外,，由于測量系統(tǒng)采用連續(xù)指數(shù)掃頻信號作為激勵信號，根據(jù)上節(jié)介紹的逆濾波器和激勵信號的關系,，再結合上文介紹的連續(xù)指數(shù)掃頻信號隨著頻率的增加,，能量不斷降低的情況，為補償其在低頻和高頻時能量的不一致,，需要對逆濾波器進行幅度調(diào)制,。采用Hilbert-Huang變換技術對激勵信號的頻譜幅值進行分析研究，根據(jù)其幅度包絡的特點在時域上對逆濾波器進行包絡調(diào)制,。下面對連續(xù)指數(shù)正弦掃頻信號的頻譜進行分析,。

　　對非線性,、非平穩(wěn)的連續(xù)指數(shù)掃頻激勵信號進行Hilbert-Huang變換,，設激勵信號x（t）時域上的解析信號Zx（t）和頻譜Zx（f）分別為：

　　其中,，H[x（t）]是x（t）的希爾伯特變換，ax（t）和x（t）分別為激勵信號的瞬時幅值和瞬時相位,，Ax（f）為激勵信號頻譜的幅值,。

　　設激勵信號的時域幅值ax（t）=1，由2.1節(jié)介紹的激勵信號的瞬時相位,，對其進行兩次求導,，再結合參考文獻[8]中公式：

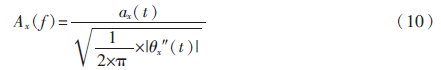
　　可得激勵信號的頻譜幅值為：

　　其中，fi為激勵信號的瞬時頻率,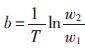，,，連續(xù)正弦掃頻信號頻域的幅度沿頻率分布的情況如圖3所示。

　　結合圖3和式（11）可知,，激勵信號的頻譜幅值是一個粉紅譜,，Ax（f）正比，頻率越低,，激勵信號幅值越大,。從能量的角度來看，激勵信號的能量從低頻向高頻不斷衰減,，與2.1節(jié)中圖2（c）介紹的激勵信號的頻譜幅值變化相一致,。

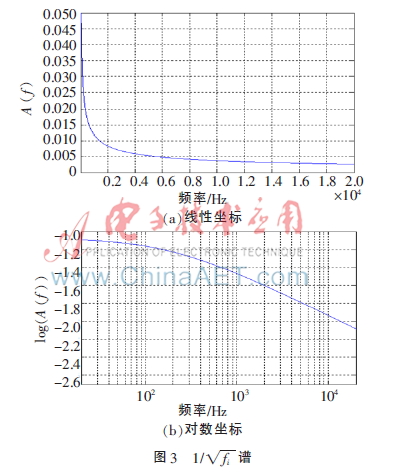
　　根據(jù)激勵信號頻譜幅值隨頻率變化的特點，在時域上對逆濾波器進行幅度調(diào)制,，求得的逆濾波器時域波形圖和頻譜如圖4所示,。

3 應用實例

　　為了驗證上述方法的有效性和快速性，將其用于揚聲器系統(tǒng)的沖激響應測量,。揚聲器系統(tǒng)測試基本框圖如圖5所示,。

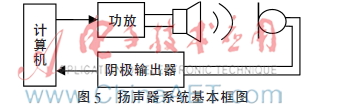
　　計算機產(chǎn)生激勵信號經(jīng)功放后加載到具有非線性特性的揚聲器，揚聲器產(chǎn)生的聲場隨后經(jīng)過空間線性傳播由傳送器接收,，接收到的信號經(jīng)陰極輸出器輸入計算機,，計算機讀取其數(shù)據(jù)，然后進行分析,、處理,。

　　采用起始頻率為20 Hz、終止頻率為20 kHz,、掃頻時間為1 s的連續(xù)指數(shù)掃頻信號作為激勵信號對揚聲器系統(tǒng)進行測試,，將系統(tǒng)響應結果與上述的逆濾波器進行卷積后，經(jīng)數(shù)據(jù)處理,，得到的揚聲器系統(tǒng)的各階沖激響應測量結果如圖6所示,。

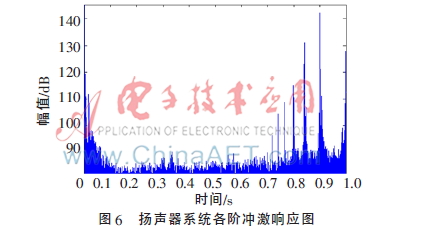
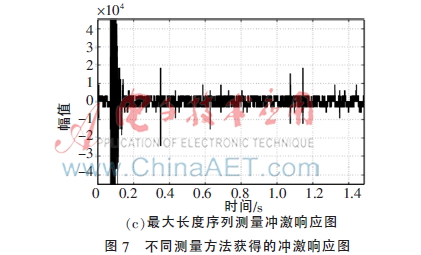
　　圖7（a）是連續(xù)指數(shù)正弦掃頻信號激勵法下的沖激響應測量結果圖,，圖7（b）和（c）分別為最大長度序列法和周期性脈沖法在室內(nèi)揚聲器系統(tǒng)下測量的沖激響應結果圖[9]。結合圖6,、圖7和參考文獻[9]可知,，連續(xù)指數(shù)正弦掃頻信號激勵法的最大特點是能夠?qū)崿F(xiàn)對非線性系統(tǒng)各階沖激響應的快速檢測，而最大長度序列法和周期性脈沖法無法將非線性系統(tǒng)中的線性與非線性響應部分分離開來,。

　　由上述可知,，圖6中從右邊開始最高幅值的是1階沖激響應即線性響應，依次向左分別為2階,、3階,、4階等更高階的沖激響應。它們以?駐ti的時間間隔依次被分隔開來,，其中?駐ti可由上述推導的式（5）所求得,，實現(xiàn)了對非線性系統(tǒng)各階沖激響應的快速檢測。

　　此外,，從圖6測量結果中可看出,，系統(tǒng)響應的噪聲在首尾處較大，這是由于激勵信號在首尾處由于信號幅度的突變而產(chǎn)生高頻能量造成的,，為改善系統(tǒng)在首尾處產(chǎn)生的噪聲,，可以對激勵信號進行加窗處理。

4 結論

　　本文從理論上對室內(nèi)聲學非線性系統(tǒng)和作為激勵信號的連續(xù)指數(shù)正弦掃頻信號,、逆濾波器的特性進行了分析研究,，通過運用上述方法對具有非線性特性的揚聲器系統(tǒng)進行實際測試，揚聲器系統(tǒng)的線性沖激響應和各階非線性沖激響應被快速地測量出來,，實現(xiàn)了對非線性系統(tǒng)各階沖激響應的快速檢測,。

參考文獻

　　[1] MULLER S， MASSARINI P. Transfer function measurement with sweeps[J]. Journal of the Audio Engineering Society,， 2001,，49（6）：443-471.

　　[2] VANDERKOOY J. Aspects of MLS measuring systems[C]. Convention of the Audio Engineering Society，1994：219-231.

　　[3] SCHETZEN M. The volterra and wiener theories of nonlinear systems[M].  New York： Wiley,， 1980.

　　[4] FARINA A. Simultaneous measurement of impulse response and distortion with a swept-sine technique[C]. 108th Convention of the Audio Engineering Society,，2000：19-22.

　　[5] ARMELLONI E， FARINA A,， BELLINI A. Non-linear convolution： a new approach for the naturalization of distorting systems[C]. 110th Convention of the Audio Engineering Society,， 2001：12-15.

　　[6] STEVE T， Brunet pascal enhancements for loose particle detection in loudspeakers[C]. 116th Convention of the Audio Engineering Society,， 2004：8-11.

　　[7] FARINA A,， RIGHINI F. Software implementation of an MLS analyzer， with tools for convolution,， naturalization and inverse filtering[C]. 103th Convention of the Audio Engineering Society,， 1997：26-29.

　　[8] COHEN L. Instantaneous frequency and group delay of a filtered signal[J]. J.Franklin Inst,， 2000，337（5）：329-346.

　　[9] BART S G,， JACQUES E J,， DOMINIQUE A. Comparison of different impulse response measurement techniques[J]. Journal of the Audio Engineering Society， 2002,，28（6）：153-157.