0 引言

    在通信系統(tǒng)中,，接收機(jī)下變頻時(shí)本振的不穩(wěn)定性以及傳輸時(shí)的多普勒效應(yīng)往往會(huì)給接收機(jī)系統(tǒng)引入頻偏誤差。這個(gè)頻偏誤差隨時(shí)間累積,，會(huì)對(duì)解調(diào)性能產(chǎn)生嚴(yán)重的影響,。

    傳統(tǒng)的解決方式是通過PLL來完成載波同步,，從根本上消除頻偏的存在，但是這種方式復(fù)雜度極高,，不便于實(shí)現(xiàn)。現(xiàn)在大多數(shù)方法是從接收到的信號(hào)中估計(jì)頻偏信息,，并進(jìn)行校準(zhǔn),。這種估計(jì)頻偏的算法分為基于數(shù)據(jù)輔助(data-aided)和非數(shù)據(jù)輔助(non-data-aided)兩大類,。

非數(shù)據(jù)輔助算法不依賴于提前知道接收到的數(shù)據(jù)信息^[1-3]，但具有估算精度較低的缺點(diǎn),。與非數(shù)據(jù)輔助算法相比,，基于數(shù)據(jù)輔助的頻偏估計(jì)算法在估算精度,、范圍以及復(fù)雜度方面都有更好的性能^[4-6]。

    圖1是低功耗藍(lán)牙BLE(Bluetooth low energy)協(xié)議定義的包格式,。其中前導(dǎo)碼為8 bit，接入地址(Access Address)為32 bit,，在解調(diào)時(shí)這40 bit的內(nèi)容都是已知的,。因此,，這里提出了一種基于數(shù)據(jù)輔助的頻偏估計(jì)和補(bǔ)償算法,。該算法結(jié)構(gòu)簡(jiǎn)單且精度高，解決了現(xiàn)有頻偏校準(zhǔn)算法中復(fù)雜度高,、系統(tǒng)延遲大以及存在殘余頻偏等缺點(diǎn),。

    本文提出了一種應(yīng)用在零中頻低功耗藍(lán)牙接收機(jī)中的GMSK解調(diào)器的結(jié)構(gòu),，重點(diǎn)研究了頻偏校準(zhǔn)算法,。

1 頻偏校準(zhǔn)算法

    眾所周知，相干解調(diào)的性能優(yōu)于非相干解調(diào),，但是復(fù)雜度較高,，在面積和功耗方面的代價(jià)較大。由于BLE協(xié)議的首要目標(biāo)是低功耗,，因此這里選擇了非相干解調(diào)的方式,。考慮到GMSK是一種恒包絡(luò)調(diào)制方式,，GMSK解調(diào)器可以通過差分解調(diào)來實(shí)現(xiàn)。

    考慮到頻偏和相偏的影響,，GMSK基帶信號(hào)可以由式(1)表示：

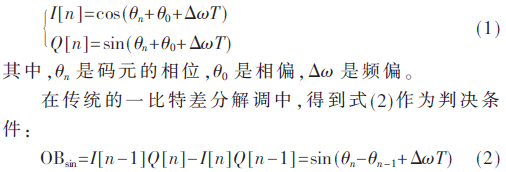
    該式與相鄰碼元的相位差成正比,，因?yàn)镚MSK的相位路徑在每個(gè)碼元區(qū)間內(nèi)是單調(diào)上升或者單調(diào)下降的，因此通過判斷OB_sin的正負(fù)就可以得到解調(diào)結(jié)果,?？梢钥吹剑诓罘诌\(yùn)算的過程中,，相偏被消除,，但是頻偏的影響依然存在，并且會(huì)對(duì)判決結(jié)果產(chǎn)生影響,。

    為了進(jìn)行頻偏估計(jì),，對(duì)傳統(tǒng)的一比特差分運(yùn)算進(jìn)行改進(jìn)，增加一條余弦支路：

    式(6)在坐標(biāo)系中,，代表了角度為ΔωT的一條直線,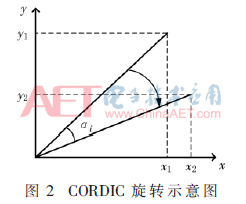，為了從中提取出ΔωT的值，使用了CORDIC算法,。CORDIC是一種逐次迭代算法,，它通過多次角度旋轉(zhuǎn)和象限判定使這條線逼近x軸，記錄下旋轉(zhuǎn)軌跡即可計(jì)算出原始角度^[7],。

    CORDIC算法每次旋轉(zhuǎn)的角度是一系列特殊的值,，符合式(7)的關(guān)系。

    如圖2所示,，在坐標(biāo)系中，順時(shí)針旋轉(zhuǎn)一個(gè)角度α_i,，可以表示為：

    聯(lián)立式(7),、式(8),，整理后可得到：

    這樣，CORDIC算法把實(shí)現(xiàn)起來困難的角度旋轉(zhuǎn)變成了簡(jiǎn)單的坐標(biāo)加減運(yùn)算,，大大降低了硬件實(shí)現(xiàn)的復(fù)雜度,。

    頻偏校準(zhǔn)的結(jié)構(gòu)圖如圖3所示。這里選擇了9級(jí)CORDIC迭代,，頻偏估計(jì)和頻偏補(bǔ)償通過2個(gè)CORDIC分別實(shí)現(xiàn),。第一個(gè)CORDIC用來進(jìn)行頻偏估計(jì),，記錄下頻偏角旋轉(zhuǎn)的路徑，第二個(gè)CORDIC通過對(duì)OB_cos+i·OB_sin進(jìn)行相同方向的旋轉(zhuǎn)完成頻偏補(bǔ)償,。

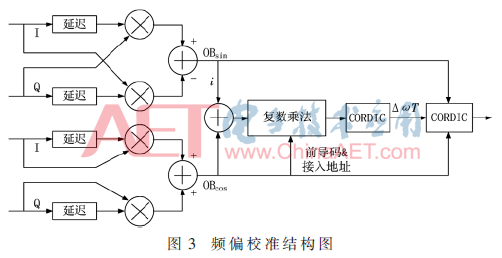
2 GMSK解調(diào)器

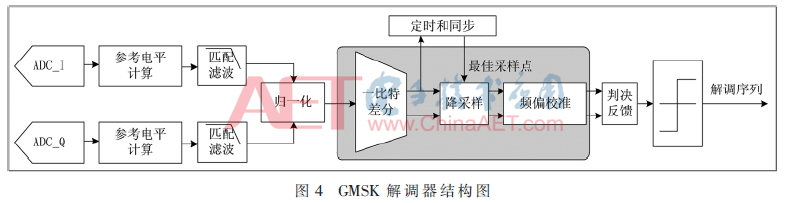
    圖4是GMSK解調(diào)器的整體結(jié)構(gòu)圖,。其中改進(jìn)的一比特差分解調(diào)和頻偏校準(zhǔn)算法在第1節(jié)中已經(jīng)詳細(xì)描述，下面主要介紹其他模塊的功能和實(shí)現(xiàn)方法,。

2.1 參考電平計(jì)算

    本文設(shè)計(jì)的GMSK解調(diào)器應(yīng)用在零中頻接收機(jī)系統(tǒng)中,，零中頻接收機(jī)引入的直流失調(diào)會(huì)嚴(yán)重影響到解調(diào)器性能。參考電平的計(jì)算就是為了消除直流失調(diào)的影響,。這里使用2 048個(gè)采樣點(diǎn)的均值作為直流失調(diào)的估算值,。

2.2 匹配濾波器

    在GMSK調(diào)制時(shí),，經(jīng)過了一個(gè)高斯成型濾波器，目的是減小發(fā)射信號(hào)的帶寬,，但同時(shí)在時(shí)域上引入了交疊,，產(chǎn)生了碼間串?dāng)_。匹配濾波的作用就是減小碼間串?dāng)_對(duì)解調(diào)的影響,，這里選擇的匹配濾波器是與成型濾波器相對(duì)應(yīng)的一個(gè)高斯濾波器,。

2.3 幅度歸一化

    中頻ADC的輸出幅度受到信號(hào)強(qiáng)度的干擾,，會(huì)在一定的范圍內(nèi)變化,，而信號(hào)幅度的變化會(huì)影響到同步相關(guān)運(yùn)算的結(jié)果。為了使同步的相關(guān)閾值更好選取,，提高同步的概率,，需要對(duì)接收到的信號(hào)幅度進(jìn)行歸一化。

    傳統(tǒng)的歸一化方式需要存儲(chǔ)大量的數(shù)據(jù),，且具有很大的延遲,，利用GMSK信號(hào)I/Q兩路的相關(guān)特性,，提出了一種新的歸一化方式，如式(11)所示：

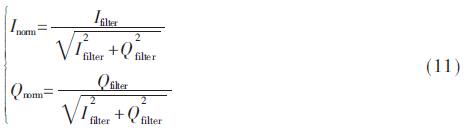
    這種歸一化方式對(duì)I/Q支路的相位信息沒有改變,，不會(huì)影響解調(diào)的結(jié)果,。除法和開方通過查找表實(shí)現(xiàn)，運(yùn)算可以在一個(gè)時(shí)鐘周期內(nèi)完成,，優(yōu)化了延遲,。

2.4 定時(shí)和同步

    ADC的采樣頻率是8 MHz，BLE規(guī)定的碼元速率是1 Mb/s,，因此對(duì)應(yīng)每個(gè)碼元有8個(gè)采樣點(diǎn),。定時(shí)就是為了從中找到最佳的采樣點(diǎn)進(jìn)行降采樣。

    GMSK信號(hào)的相位路徑在一個(gè)碼元周期中是單調(diào)上升或者單調(diào)下降的,，因此根據(jù)式(2),，一比特差分運(yùn)算的正弦支路OB_sin在一個(gè)碼元周期內(nèi)也是單調(diào)變化的。因此可以找到一個(gè)采樣點(diǎn),，使得在一段長(zhǎng)度內(nèi)累積OB_sin的絕對(duì)值之和達(dá)到最大值,，此時(shí)OB_sin離判決門限最遠(yuǎn)，減少了誤判的概率,，即把該點(diǎn)作為最佳采樣點(diǎn)^[8],。

    同步的目的是在接收到的序列中找到包頭的位置，這里通過滑動(dòng)相關(guān)來實(shí)現(xiàn),。首先把接收到的40 bit數(shù)據(jù)與圖1中的前導(dǎo)碼以及接入地址做相關(guān)運(yùn)算,，如果相關(guān)結(jié)果小于閾值，則數(shù)據(jù)向后滑動(dòng)一個(gè)碼元,，重復(fù)相關(guān)運(yùn)算,，直到相關(guān)結(jié)果超過閾值實(shí)現(xiàn)數(shù)據(jù)的同步。

2.5 判決和解調(diào)

    考慮到GMSK的碼間串?dāng)_特性,，采用了判決反饋算法來完成解調(diào)^[9],。

    正如在第2小節(jié)討論的，第n位的相鄰碼元相位差會(huì)受到第n+1位和第n-1位的影響,。因?yàn)榻庹{(diào)是順序進(jìn)行的,，在解調(diào)x[n]時(shí)，x[n-1]是已知的,，因此可以根據(jù)x[n-1]的值對(duì)x[n]的判決條件進(jìn)行修正,，進(jìn)而減小碼間串?dāng)_的影響。

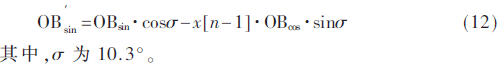
3 仿真結(jié)果及討論

    根據(jù)BLE協(xié)議的規(guī)定,，在一個(gè)數(shù)據(jù)包內(nèi),，頻偏最大不超過±150 kHz。針對(duì)各種不同的頻偏情況，本文仿真了GMSK解調(diào)器的誤碼率曲線,。這里使用的GMSK信號(hào)BT參數(shù)為0.5,，每一個(gè)數(shù)據(jù)包長(zhǎng)度為376 bit，每個(gè)點(diǎn)的誤碼率通過3 000包數(shù)據(jù)仿真得到,，且假設(shè)信號(hào)在加性高斯白噪聲信道傳輸,。

    圖5是有無頻偏校準(zhǔn)情況下對(duì)比的誤碼率曲線圖。其中三角標(biāo)記的為理想沒有頻偏情況下的誤碼率曲線,，圓形標(biāo)記的為50 kHz頻偏且沒有做頻偏校準(zhǔn)情況下的誤碼率曲線,，而方形標(biāo)記的為50 kHz頻偏且做了頻偏校準(zhǔn)情況下的誤碼率曲線?？梢钥闯鲱l偏校準(zhǔn)對(duì)解調(diào)器的性能有很大的影響,，在10^-2誤碼率條件下，解調(diào)器性能改善了約6 dB,。

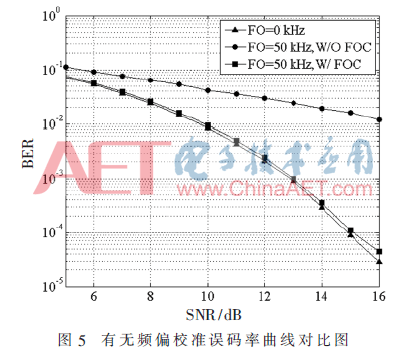
    圖6是在0 kHz,、50 kHz、100 kHz以及150 kHz頻偏條件下的誤碼率曲線,。

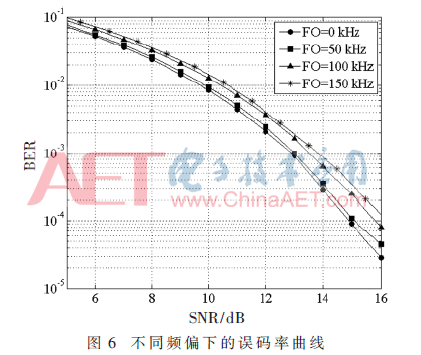
    其中圓形標(biāo)記的為理想沒有頻偏情況下的誤碼率曲線,，要達(dá)到BLE協(xié)議規(guī)定的10^-3誤碼率要求，需要12.8 dB的SNR,，優(yōu)于傳統(tǒng)的差分解調(diào)需要的15 dB信噪比的性能,。

    方形、三角和米字標(biāo)記的分別是50 kHz,、100 kHz以及150 kHz頻偏下的誤碼率曲線,。可以看出,，頻偏在50 kHz以內(nèi)時(shí),，誤碼率曲線與理想情況幾乎重合。在最大150 kHz頻偏條件下,，要達(dá)到10^-3誤碼率,，需要13.7 dB的SNR，與理想情況相比,，解調(diào)器性能下降在1 dB以內(nèi),。

該算法同樣適用于負(fù)頻偏的情況，其性能與正頻偏時(shí)完全相同,。

4 結(jié)論

    本文設(shè)計(jì)了一款應(yīng)用在零中頻低功耗藍(lán)牙接收機(jī)中的GMSK解調(diào)器,。重點(diǎn)介紹了一種新的頻偏校準(zhǔn)的算法，通過把改進(jìn)的一比特差分解調(diào)和CORDIC算法結(jié)合,，可以有效地處理150 kHz以內(nèi)的頻偏干擾,；通過CORDIC旋轉(zhuǎn)和對(duì)差分運(yùn)算模塊復(fù)用降低了硬件開銷。設(shè)計(jì)由Verilog語言實(shí)現(xiàn),，并通過FPGA驗(yàn)證,，結(jié)果表明該解調(diào)器誤碼率性能優(yōu)良，硬件復(fù)雜度低,，適合應(yīng)用于低功耗藍(lán)牙通信系統(tǒng)中,。

參考文獻(xiàn)

[1] Yao Yingwei，GIANNAKIS G B.Blind carrier frequency offset estimation for OFDMA-based wireless networks[C].IEEE Military Communications 2004：1233-1239.

[2] Zhang Xiupei,，RYU H G,，JO B G，et al.Analyses and suppression method of frequency offset and timing offseet in FH-OFDM system[C].First International Conference on Advances in Satellite and Space Communications.Colmar,，F(xiàn)rance,，2009：123-127.

[3] RAMLALL R.Non-data-aided joint estimation of time and frequency offset in OFDM systems using channel order based regression[C].IEEE Military Communications Conference.San Diego，USA,，2013：73-77.

[4] LIN J N,，CHEN H Y，WEI T C,，et al.Symbol and carrier frequency offset synchronization for IEEE802.16e[C].IEEE International Symposium on Circuit and Systems.Seattle,，USA，2008：3082-3085.

[5] FUSCO T,，PETRELLA A,，TANDA M.Data-aided symbol timing and CFO synchronization for filter bank multicarrier systems[J].IEEE Transactions on Wireless Communications，2009,，8(5)：2705-2715.

[6] Liu Jingxian,，Hao Jinxing，Wang Jintao.A low complexity frequency offset estimation for dual PN TDS-OFDM[C].IEEE International Symposium on Broadband Multimedia Systems and Broadcasting.Ghent,，Belgium,，2015：1-4.

[7] 楊宏，李國(guó)輝,，劉立新.基于FPGA的CORDIC算法的實(shí)現(xiàn)[J].西安郵電學(xué)院學(xué)報(bào),，2008，13(1)：75-77.

[8] 賴文強(qiáng),，趙建業(yè).一種面向DSP實(shí)現(xiàn)的GMSK位同步算法[J].無線電工程,，2004，3(2)：12-14,，61.

[9] YONGACOGLU A,，MAKRAKIS D，KAMILO F.Differential detection of GMSK using decision feedback[J].IEEE Transactions on Communications,，1988,，36(6)：641-649.