文獻(xiàn)標(biāo)識(shí)碼: A
DOI:10.16157/j.issn.0258-7998.2016.09.004
中文引用格式: 王建中,楊璐. 基于GPS定向測(cè)姿系統(tǒng)的研究[J].電子技術(shù)應(yīng)用,2016,42(9):14-18.
英文引用格式: Wang Jianzhong,Yang Lu. Research on GPS orientation attitude measurement system[J].Application of Electronic Technique,2016,42(9):14-18.
0 引言
GPS又稱為“衛(wèi)星測(cè)時(shí)測(cè)距導(dǎo)航全球定位系統(tǒng)”,由24顆高度約20 000 km的人造衛(wèi)星組成[1]。24顆衛(wèi)星專門用于定位,分布在以地球?yàn)橹行牡牧鶄€(gè)軌道面上(每軌道面四顆),能夠提供24小時(shí)連續(xù)的定位和導(dǎo)航服務(wù),其接收終端具有定位、授時(shí)的能力[2]。目前,GPS在定位上應(yīng)用較普遍,定向、測(cè)姿的應(yīng)用在起步階段,存在以下問(wèn)題:
(1)功能單一、大部分只具有定位功能,不能夠定向和測(cè)量載體姿態(tài)[3]。
(2)價(jià)格相當(dāng)昂貴。大部分定向、測(cè)姿態(tài)設(shè)備采用慣性導(dǎo)航系統(tǒng)[4],價(jià)格超過(guò)100萬(wàn)元。
(3)輸出信息不具有二次開發(fā)性。
(4)信息輸出不具有實(shí)時(shí)、可靠、準(zhǔn)確、快速性。
(5)坐標(biāo)輸出信息不全,與外接設(shè)備無(wú)信息交換。
因此,研究一種集定位定向、測(cè)姿功能的系統(tǒng)十分必要。
1 GPS定向測(cè)姿相關(guān)理論研究
1.1 利用載波相位測(cè)量建立誤差方程
GPS衛(wèi)星信號(hào)接收機(jī)有很多種類,一般都有兩類基本的觀測(cè)量:一個(gè)是偽距觀測(cè)量,另一個(gè)是載波相位觀測(cè)量[5]。
GPS載波分為:L1,其波長(zhǎng)為0.19 m,頻率為1 575.42 MHz,觀測(cè)誤差為1.9 m[6]。
設(shè)GPS的衛(wèi)星j在t0時(shí)刻發(fā)射信號(hào),經(jīng)過(guò)時(shí)間t后于ti時(shí)刻被GPS終端機(jī)接收, 為t對(duì)應(yīng)的相位差,
為t對(duì)應(yīng)的相位差,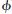 j(ti)為GPS衛(wèi)星載波信號(hào)在t時(shí)刻的相位,
j(ti)為GPS衛(wèi)星載波信號(hào)在t時(shí)刻的相位, i(ti)為接收機(jī)本地信號(hào)在時(shí)刻的相位,則:
i(ti)為接收機(jī)本地信號(hào)在時(shí)刻的相位,則:

其中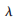 為波長(zhǎng)。
為波長(zhǎng)。
衛(wèi)星與接收終端機(jī)之間的相位差一般由整數(shù)和小數(shù)兩部分組成:
![$]]XFB4WKKTE4A0`(7C@0[Y.png $]]XFB4WKKTE4A0`(7C@0[Y.png](http://files.chinaaet.com/images/2016/10/29/6361336002838700009105776.png)
其中,N0為整周相位數(shù), 為不足一個(gè)整周相位部分。
為不足一個(gè)整周相位部分。
在接收機(jī)的鑒相器中,只能測(cè)出小數(shù)的部分。
ti時(shí)刻GPS衛(wèi)星到接收機(jī)的載波相位為:
![Q]7`QJZS@RR_V638S}S4I33.jpg Q]7`QJZS@RR_V638S}S4I33.jpg](http://files.chinaaet.com/images/2016/10/29/6361336007807400006825051.jpg)
其中,N0為載波相位測(cè)量中出現(xiàn)了一個(gè)整周未知數(shù)。接收終端機(jī)鎖定并實(shí)時(shí)跟蹤衛(wèi)星信號(hào)后,并不斷測(cè)定載波相位的變化,在ti時(shí)刻利用多普勒計(jì)數(shù)器記錄, Nk為ti時(shí)刻到tk時(shí)刻相位整周變化量。
Nk為ti時(shí)刻到tk時(shí)刻相位整周變化量。
載波相位測(cè)量只能測(cè)量小數(shù)部分,原因有多種,其中可能產(chǎn)生整周跳變現(xiàn)象,例如接收機(jī)天線被遮擋、衛(wèi)星數(shù)量過(guò)少、信號(hào)丟失、外界噪聲信號(hào)的干擾等。理論上可以通過(guò)數(shù)據(jù)處理如濾波來(lái)解決一些問(wèn)題,但濾波是有代價(jià)的,數(shù)據(jù)不能實(shí)時(shí)反應(yīng)載體的運(yùn)動(dòng)狀態(tài),實(shí)現(xiàn)也很復(fù)雜[7]。
在實(shí)際應(yīng)用中,如GPS應(yīng)用在車上、船舶、飛機(jī)等載體,GPS接收機(jī)由于多路徑誤差、時(shí)鐘等多種信號(hào)經(jīng)常在非真空中傳播,會(huì)遇到不同的復(fù)雜情況,還可能出現(xiàn)電離層、對(duì)流層延時(shí)誤差、接收機(jī)測(cè)量噪聲等多種原因,造成GPS載波相位測(cè)量中存在著誤差[8]。誤差測(cè)量方程為:
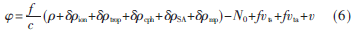
1.2 GPS定位技術(shù)理論分析
GPS定位分為絕對(duì)定位和相對(duì)定位,即為單點(diǎn)定位和差分定位,精度要求較高,尤其是大地測(cè)繪或軍事應(yīng)用采用相對(duì)定位,一般精度都在厘米級(jí),需要8個(gè)以上的通道才能夠保證精度,跟蹤衛(wèi)星超過(guò)7顆。
基本觀測(cè)方程為[9]:
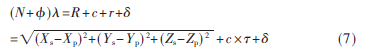
其中, 為相位觀測(cè)量;R為接收機(jī)到衛(wèi)星的距離;r為接收機(jī)鐘差;為對(duì)流層和電離層的延遲。式(7)中,?準(zhǔn)是相位小數(shù),N是相位整周數(shù)信號(hào)通過(guò)對(duì)流層、電離層的延遲修正;(Xs,Ys,Zs)為衛(wèi)星的瞬時(shí)相對(duì)于地心坐標(biāo);(Xp,Yp,Zp)為接收終端機(jī)到地心坐標(biāo)。
為相位觀測(cè)量;R為接收機(jī)到衛(wèi)星的距離;r為接收機(jī)鐘差;為對(duì)流層和電離層的延遲。式(7)中,?準(zhǔn)是相位小數(shù),N是相位整周數(shù)信號(hào)通過(guò)對(duì)流層、電離層的延遲修正;(Xs,Ys,Zs)為衛(wèi)星的瞬時(shí)相對(duì)于地心坐標(biāo);(Xp,Yp,Zp)為接收終端機(jī)到地心坐標(biāo)。
GPS終端機(jī)的接收天線假如安裝在T1、T2兩個(gè)固定點(diǎn)或測(cè)站上,它們?cè)谕粫r(shí)刻同時(shí)觀測(cè)到星歷數(shù)據(jù)[10],利用數(shù)據(jù)處理單元記錄并建立相位觀測(cè)量,從而得到基本單差觀測(cè)方程:

上標(biāo)為衛(wèi)星號(hào),下標(biāo)為測(cè)站號(hào),由此可以看出,利用同一時(shí)刻觀測(cè)的兩顆衛(wèi)星的單差方程式來(lái)求解雙差(DD)的觀測(cè)方程。
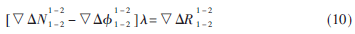
式(10)雙差觀測(cè)方程中是基線向量與相位整周數(shù)差值部分。相位整周數(shù)一般情況不會(huì)發(fā)生變化,不受時(shí)間和地點(diǎn)發(fā)生變化。可以根據(jù)相鄰兩個(gè)雙差觀測(cè)方程得到三差觀測(cè)方程。
2 GPS定向測(cè)姿系統(tǒng)實(shí)現(xiàn)
利用車輛的航向、橫滾、俯仰描述車體運(yùn)動(dòng)是基于真北向與水平位置的關(guān)系,其中載體航向是載體基于地理坐標(biāo)系中載體中軸線與真北向的夾角稱為航向。車輛坐標(biāo)X、Y、Z是游動(dòng)坐標(biāo)系(b系)和地理坐標(biāo)系(n系)之間坐標(biāo)轉(zhuǎn)換,其方位與它們有一個(gè)夾角關(guān)系[11]。因此,地理坐標(biāo)系為北東天地坐標(biāo)系,游動(dòng)坐標(biāo)系xb軸指向車輛前進(jìn)方向,也就是說(shuō)我們載體的航向,yb指向車輛的前進(jìn)方向車輛側(cè)面,也就是說(shuō)載體的橫滾;zb指向車輛的底盤下方,這樣就構(gòu)成了東北天地的坐標(biāo)系。則航向角以北向向東向偏轉(zhuǎn)為正,反方向?yàn)樨?fù);俯仰角?茲以向上為正;橫滾角以載體坐標(biāo)系xb軸方向?yàn)檎喾礊樨?fù)[12]。
游動(dòng)坐標(biāo)系和地理坐標(biāo)系之間的轉(zhuǎn)換矩陣為:
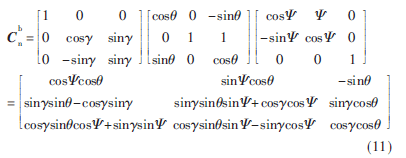
C為姿態(tài)矩陣,是地理坐標(biāo)系和游動(dòng)坐標(biāo)系之間的方位關(guān)系。
![~Y6LS{%V_XLR[TVD]5X)4L4.png ~Y6LS{%V_XLR[TVD]5X)4L4.png](http://files.chinaaet.com/images/2016/10/29/6361336028134900007422423.png)
俯仰角的取值范圍在±90°范圍內(nèi),與三角函數(shù)中的反正弦函數(shù)值一樣,有區(qū)間問(wèn)題,但值只有正負(fù)之分。而航的定義域?yàn)?°~360°區(qū)間內(nèi),橫滾角的定義域?yàn)?180°~+180°區(qū)間,所以得到求解的姿態(tài)角存在象限判斷問(wèn)題,判斷方法如表1、表2所示。


2.2 GPS單基線方位角解算及誤差分析
所謂單個(gè)基線就是只有一條基線,本論文利用6 m長(zhǎng)的基線,解算航向和俯仰。一條基線沿載體的縱軸安裝,解算出航向角和俯仰角,如果再加一根基線只沿載體的橫軸安裝,則可以解算出橫滾角,本論文采用單基線三個(gè)GPS的安裝方法[13]。
將基線沿載體的實(shí)際中軸線安裝,也就是說(shuō)基線向量在車輛坐標(biāo)系中的坐標(biāo)表示為Rb=[b 0 0]T,b是基線長(zhǎng)度,單位為m,本論文中基線的長(zhǎng)度設(shè)計(jì)為6.00 m,基線向量在地理坐標(biāo)系中的坐標(biāo)為Rn=[xn yn zn]T,則根據(jù)式(13)并根據(jù)姿態(tài)矩陣C的正交性,可以得到航向角、俯仰角的估計(jì)值:

其數(shù)值的范圍為:

由上推出,航向角及俯仰角的解算精度與基線的長(zhǎng)度成反比,理論上基線越長(zhǎng)精度越高,但是,選擇的GPS基線長(zhǎng)度不可能無(wú)限長(zhǎng),我們只能在合理的區(qū)間選擇。通過(guò)固定基線,求解航向、姿態(tài),直接由XDOP、YDOP、ZDOP作為對(duì)角線元素構(gòu)成的對(duì)角矩陣稱為姿態(tài)精度因子矩陣。
2.3 GPS雙基線姿態(tài)解算方法
如果有三個(gè)或多個(gè)不共線的GPS接收機(jī)天線,組建成互相垂直的兩條基線,這兩條基線可以在自己的坐標(biāo)系內(nèi),通過(guò)信號(hào)接收板接收到4顆以上衛(wèi)星,就可以聯(lián)立方程解算出全部載體的航向、橫滾、俯仰角。本小節(jié)利用基本算法解算姿態(tài)矩陣C,從而解算出姿態(tài)參數(shù)。
兩條基線安裝車體上,在游動(dòng)坐標(biāo)系中的坐標(biāo)中設(shè)為Rb1、Rb2,在地理坐標(biāo)系中的坐標(biāo)設(shè)為Rn1、Rn2。
通過(guò)建立三個(gè)互相正交的矢量,聯(lián)立求解,分別為:
![V4OI8XFS~4Z3G]__YNVXNPF.png V4OI8XFS~4Z3G]__YNVXNPF.png](http://files.chinaaet.com/images/2016/10/29/6361336042098300006554800.png)
同樣可以在地理坐標(biāo)系中建立三個(gè)互相正交的矢量:

如果兩個(gè)基線向量不平行,所以矩陣從滿秩,是可逆的,由式(24)可以解算出姿態(tài)矩陣:
![6%H_()%[5JFHO6YBN4])G%L.png 6%H_()%[5JFHO6YBN4])G%L.png](http://files.chinaaet.com/images/2016/10/29/6361336045338300007478245.png)
從而解算出三個(gè)姿態(tài)角,即航向、橫滾、俯仰。為了減少誤差,盡量保持兩條基線垂直,用轉(zhuǎn)角直尺來(lái)校準(zhǔn);基線長(zhǎng)度按需求盡量長(zhǎng),一般采用6 m基線,測(cè)量基線長(zhǎng)度采用多測(cè)幾次求平均值的方法;解算采用雙精度浮點(diǎn)運(yùn)算。
3 利用最小乘法求解整周模糊度及姿態(tài)確定
采用了三個(gè)GPS接收天線,并將天線安裝一根長(zhǎng)度為6 m的鋁合金基線上,天線安裝需在同一條直線上,其中兩個(gè)最短的GPS接收天線相距14 cm,用于粗尋北,最長(zhǎng)的兩個(gè)GPS接收天線相距6.00 m,用于精尋北。當(dāng)衛(wèi)星數(shù)據(jù)超過(guò)4顆時(shí),10 s內(nèi)解算出直線的初始方向,1 min內(nèi)確定初始模糊度,以此確定搜索范圍,快速搜索出擬合殘差小于給定值的閾值內(nèi)解的集合,最后確定擬合殘差優(yōu)選出最優(yōu)解[14]。
3.1 GPS模糊度的搜索范圍
衛(wèi)星空間布局確定搜索范圍,雙差方程可以寫為:
Qi=Hi1X1+Hi2X2+Hi3X3+Ni(26)
要求其N的范圍,只須求出H1 X1、H2 X2、H3 X3的范圍,由于:
![O~M[EB$L]{R79W$KDLD2PR0.png O~M[EB$L]{R79W$KDLD2PR0.png](http://files.chinaaet.com/images/2016/10/29/6361336051369900005943779.png)
根據(jù)求條件值理論可以求得:
![[QN$_A~S_4EP]6JHPOSV`(H.png [QN$_A~S_4EP]6JHPOSV`(H.png](http://files.chinaaet.com/images/2016/10/29/6361336047579000001825241.png)
求解確定模糊度范圍,把模糊度看作待求值,由式(26)中的雙差型方程,可以改寫為:
![@{9]48@ZCJNQAT(P)(X3{GO.png @{9]48@ZCJNQAT(P)(X3{GO.png](http://files.chinaaet.com/images/2016/10/29/6361336054375600008360863.png)
由式(26)、式(29)求交集可以得出模糊度N的范圍。
3.2 GPS模糊度的最優(yōu)判定及載波整周數(shù)
模糊度的最優(yōu)判定是一個(gè)難點(diǎn)。由于衛(wèi)星信號(hào)在傳輸過(guò)程中的各種干擾和接收機(jī)本身的噪聲,使得有時(shí)真值不一定是最優(yōu)解。
根據(jù)數(shù)理統(tǒng)計(jì)理論:次優(yōu)殘差平方和與最優(yōu)殘差平方和之比服從χ2分布。模糊判斷如下:
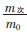 ≈x2,判別準(zhǔn)則為:
≈x2,判別準(zhǔn)則為: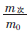 >k則判最優(yōu)解為真值;
>k則判最優(yōu)解為真值; <k則需要延長(zhǎng)時(shí)間重新計(jì)算。k值的取值需要遵循數(shù)理統(tǒng)計(jì)規(guī)律和實(shí)際測(cè)試情況綜合確定。
<k則需要延長(zhǎng)時(shí)間重新計(jì)算。k值的取值需要遵循數(shù)理統(tǒng)計(jì)規(guī)律和實(shí)際測(cè)試情況綜合確定。
載波整周數(shù):相位測(cè)量?茲i,最小的ni和X,根據(jù)最小二乘擬合計(jì)算X。

3.4 快速確定航向
根據(jù)一點(diǎn)坐標(biāo)和方向矢量,進(jìn)行坐標(biāo)轉(zhuǎn)換可以確定北向方向。
(1)求A=(X1,Y1,Z1)T的地心坐標(biāo)求解A點(diǎn)的經(jīng)度。

4 實(shí)測(cè)驗(yàn)證
GPS定位測(cè)姿系統(tǒng)與測(cè)繪局測(cè)量的標(biāo)準(zhǔn)點(diǎn)對(duì)比測(cè)量定位精度,多次測(cè)試航向、俯仰重復(fù)性精度,動(dòng)態(tài)測(cè)量采用測(cè)繪局實(shí)測(cè)標(biāo)準(zhǔn)點(diǎn)與慣性導(dǎo)航測(cè)量姿態(tài)結(jié)合測(cè)量定位、定向、俯仰精度。
4.1 定位情況及結(jié)果對(duì)對(duì)比圖
驗(yàn)證GPS定向測(cè)姿系統(tǒng)定位精度,采用測(cè)繪局實(shí)測(cè)標(biāo)準(zhǔn)點(diǎn)為基準(zhǔn),精度在10 cm內(nèi),在衛(wèi)星信號(hào)達(dá)到7顆以上的情況實(shí)測(cè)10 min,GPS定位測(cè)姿系統(tǒng)采用差分方式,CEP精度高于5 cm;GPS單點(diǎn)定位CEP精度超過(guò)10 m。測(cè)試結(jié)果如圖1,單位為度。

4.2 轉(zhuǎn)臺(tái)測(cè)試情況及結(jié)果
將GPS接收天線基線固定高精度轉(zhuǎn)臺(tái)上,基線長(zhǎng)6 m。在不同的方向上連續(xù)測(cè)試。試驗(yàn)結(jié)果符合技術(shù)要求。見表3。

4.3 動(dòng)態(tài)跑車實(shí)驗(yàn)結(jié)果
將GPS的6 m長(zhǎng)的基線架在車上,基線安裝在車的中軸線上,先標(biāo)定基線與車中軸線的安裝夾角后,然后進(jìn)行實(shí)驗(yàn)。以高精度差分GPS為標(biāo)準(zhǔn)測(cè)量其定位精度,以高精度航姿設(shè)備為標(biāo)準(zhǔn)(精度超過(guò)0.1 mil),標(biāo)安裝誤差后,連續(xù)多次動(dòng)態(tài)實(shí)驗(yàn)結(jié)果,經(jīng)過(guò)多次動(dòng)態(tài)實(shí)驗(yàn)結(jié)果詳見表4。

從上表實(shí)驗(yàn)結(jié)果說(shuō)明該系統(tǒng)動(dòng)態(tài)定位精度、動(dòng)態(tài)航向精度與標(biāo)準(zhǔn)系統(tǒng)航向誤差小于1 mil。
5 總結(jié)
通過(guò)對(duì)GPS技術(shù)應(yīng)用研究,運(yùn)用載波相位測(cè)量原理、定位技術(shù)理論分析、衛(wèi)星位置計(jì)算等相關(guān)理論知識(shí),建立定向測(cè)姿系統(tǒng)載波相位觀測(cè)方程,分析了單基線方位角解算及誤差,推導(dǎo)了利用單基線解算方位角和俯仰角以及利用雙基線解算全姿態(tài)角的方法,提出整周模糊度快速解算的新方法,利用三角函數(shù)約束條件減少整周模糊度的搜索范圍,篩選指標(biāo)不受基線運(yùn)動(dòng)的狀態(tài)影響來(lái)進(jìn)行平差,以及利用最小二乘法用于整周模糊度問(wèn)題快速確定模糊度范圍、模糊度的搜索及其模糊度的最優(yōu)判定,最后計(jì)算出最優(yōu)解,達(dá)到GPS快速確定最優(yōu)航向和俯仰角效果。
參考文獻(xiàn)
[1] 范勝林.GPS姿態(tài)及定向系統(tǒng)的研究與實(shí)現(xiàn)[D].南京:南京航空航天大學(xué),2001.
[2] 王惠南.GPS導(dǎo)航原理與應(yīng)用[M].北京:科學(xué)出版社,2003:206-243.
[3] Kendall Ferguson,Joanna Kosmalska,Hark kuhl,et al.Three-Dimensional attitude detemination,with the ashtech 3DF 24-channel GPS Measurement System[C].Proceedings of 47th Annual Technical Meeting on Using Synergism to Strengthen Navigation System 1991:35-41.
[4] 陳小明.高精度GPS動(dòng)態(tài)定位的理論與實(shí)踐[D].武漢:武漢測(cè)繪大學(xué).1997.
[5] 黃丁發(fā),卓健成.GPS相位觀測(cè)值周跳檢測(cè)的小波分析法[J].測(cè)繪學(xué)報(bào),1997,6(4):352-357.
[6] 胡國(guó)輝,孟浩,袁信.差分GPS載波相位測(cè)量整周模糊度的快速求解[J].航空學(xué)報(bào),1999(2):127-129.
[7] 章仁為.衛(wèi)星軌道姿態(tài)動(dòng)力學(xué)與控制[M].北京:北京航空航天大學(xué)出版社,1998.
[8] 廖向前,黃吉順,黃曉玲.G玲雙基線載體姿態(tài)側(cè)量研究[J].骯空學(xué)報(bào).1998,19(5):531-535.
[9] 胡國(guó)輝,孟浩,袁信.差分GPS載波相位測(cè)量整周模糊度的快速求解[J].航空學(xué)報(bào),1999(2):127-129.
[10] 李海峰,孫付平.衛(wèi)星導(dǎo)航接收機(jī)測(cè)試場(chǎng)景軟件的設(shè)計(jì)與實(shí)現(xiàn)[J].中國(guó)慣性學(xué)報(bào),2008,16(2):183-187.
[11] 廖向前,黃吉順.一種GPS動(dòng)態(tài)解相位模糊的搜索算法[J].電子科技大學(xué)學(xué)報(bào),1997,26(4):13-17.
[12] 逯亮清,胡小平,吳美平.利用旋轉(zhuǎn)基線方法進(jìn)行雙星快速定向[J].宇航學(xué)報(bào),2004,25(2).
[13] 武靜.基于非線性模型的單機(jī)GPS定位估計(jì)方法的研究[D].上海:上海交通大學(xué),2007.
[14] 姚勇,張春.GPS載波相位差分技術(shù)實(shí)時(shí)測(cè)姿的研究與應(yīng)用[J].中國(guó)慣性學(xué)報(bào),2003,6(3):21-23.

