MIMO和OFDM技術(shù)結(jié)合能有效提高系統(tǒng)頻譜效率并克服無線信道中嚴重的頻率選擇性衰落,，是下一代無線通信的關(guān)鍵技術(shù)[1],。在MIMO-OFDM系統(tǒng)中，有最優(yōu)檢測性能的極大似然檢測算法ML(Maximum Likelihood)及球譯碼算法[2]復(fù)雜度高,?；谄攘鉠F(Zero Forcing)和最小均方誤差MMSE(Minimum Mean Square Error)的線性信號檢測算法復(fù)雜度低，但當(dāng)信道條件較差時,，將產(chǎn)生噪聲放大效果,。目前針對MIMO系統(tǒng)，采用格點減少算法[3-4]對信道矩陣做預(yù)處理,，算法復(fù)雜度低且能有效提高檢測性能[5-7],。但在MIMO-OFDM系統(tǒng)中，信道矩陣變化快,，這將產(chǎn)生大量列交換迭代,。本文通過改進LLL算法并與排序的QR分解結(jié)合，先對信道矩陣做排序的QR分解得到上三角矩陣R,其對角線元素的模具有較好的升序排列,，再對R進行LLL算法處理,，處理中不再進行列交換運算，從而省去LLL算法中的迭代,，大大減少了計算復(fù)雜度,。

1 系統(tǒng)模型

　　考慮MIMO-OFDM系統(tǒng)發(fā)送端和接收端分別有NT和NR(NR≥NT)個天線。假設(shè)傳播信道為頻率選擇性信道,，每個發(fā)射天線和接收天線間的信道衰落獨立,。接收端在多路頻域信號流的同一子載波上采用MIMO接收算法檢測。系統(tǒng)模型可表示為：

　　yi=Hisi+zi   (1)

　　其中,，si代表第i個子載波上的NT×1發(fā)送信號矢量,，E{(si)(si)H}=I；yi表示第i個子載波上的NR×1接收信號矢量,；NR×1維矢量zi代表各維獨立的高斯白噪聲,，E{(zi)(zi)H}=z2I;Hi代表NR×NT信道矩陣，其元素為單位方差互不相關(guān)的復(fù)高斯衰落增益,，假設(shè)Hi幀內(nèi)保持不變,，幀間獨立變化,。

　　若分別處理式(1)中實部和虛部，省略上標(biāo),，信道模型可轉(zhuǎn)化為：

　　y=Hs+z   (2)

　　其中實值矩陣H為：

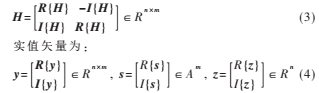
　　R{·}和I{·}代表取實部和取虛部,，n=2NR和m=2NT代表維數(shù), A代表有限實數(shù)集。

2 格點減少算法

　　在實數(shù)信道模型中,，假設(shè)發(fā)送信號矢量的各維為整數(shù),，則所有可能的無噪聲接收信號Hs可視為一個格點集，該集以H的列矢量為基矢量,，每個格點都是這些基矢量的線性組合,。同時該格點集也可用矩陣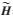=HT的列矢量為基矢量表示，T為幺模矩陣,。采用QR分解,，H=QR，系統(tǒng)方程(2)可寫為:

　　y=QRs+z   (5)

　　矩陣條件數(shù)定義為k(H)=max/min=‖H‖2‖H-1‖2≥1,，

　　max,、min為H的最大和最小奇異值,。通常信道矩陣條件數(shù)越大,，噪聲放大越大，線性檢測的判決域也越狹小;相反,，對正交矩陣k(H)=1,，將無噪聲放大，判決域也最大,。式(5)中,， Q是酉矩陣， ‖QR‖2=‖RQ‖2=‖R‖2,， k(H)=‖QR‖2‖R-1Q‖2=‖R‖2‖R-1‖2=k(R),，所以H和R有相同條件數(shù)。格點減少算法的目標(biāo)是找到一個等效的系統(tǒng)方程,，其信道矩陣的條件數(shù)小于R的條件數(shù),。

　　基于R矩陣的LLL算法便是一種有效的格點減少算法。LLL減少的兩個條件為：

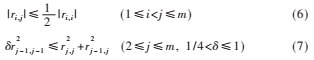
　　其中ri,j為R矩陣第i行j列元素,，取值0.75具有最佳約減效果[2],。式(6)使基矢量的模減小，矩陣條件數(shù)減小,。式(7)將新基矢量與原基矢量比較,，進一步減小模，使各基矢量更接近正交,。通過LLL算法處理得到約減的矩陣RLLL,，此時系統(tǒng)方程(5)可寫為：

　　新系統(tǒng)方程將被認為是條件良好的,，對其線性檢測時，噪聲放大減小,，判決域增大,。

3 改進的格點減少算法

　　3.1 約減LLL算法分析

　　LLL算法復(fù)雜度主要取決于為滿足式(7)而進行的列交換迭代次數(shù)。最壞時,，隨天線數(shù)增加,，復(fù)雜度是無界的[2]。參考文獻[5]指出,，在4×4天線配置下,，傳統(tǒng)LLL算法平均列交換次數(shù)為13.2次，若FFT長度為64,，則每幀MIMO-OFDM信號將產(chǎn)生844.8=64×13.2次列交換,。

　　信道矩陣H的元素都是獨立的高斯變量，經(jīng)過式(6)處理后各列矢量間高度相關(guān)的概率較小,，因此當(dāng)約減的LLL算法只采用式(6)進行矢量模減小,，然后對新的信道矩陣采用線性檢測時,將得到一個較大的判決域，而噪聲放大也不是很大,通常能得到較好的誤碼率曲線,。且因省去列交換的迭代,，算法復(fù)雜度大大減小。

　　3.2 約減LLL算法和排序QR分解結(jié)合檢測

　　當(dāng)信道矩陣的維數(shù)較小時,，矩陣元素的初始值易使式(6)恒成立,，采用約減的LLL算法將使矩陣得不到約減。為使約減性能達到LLL算法,，并避免其算法的大量迭代,，在約減的LLL算法前，先對信道矩陣進行wubben排序QR分解[8],。它在QR分解過程中排序,，使R矩陣的對角線元素的模|ri,j|盡可能從小到大排列。這樣,，R矩陣中大部分元素滿足式(7),此時采用約減的LLL算法將達到LLL算法的性能,。參考文獻[8]指出排序的QR分解的計算開銷和未排序的QR分解相比幾乎可忽略。因此在4×4天線配置下,，排序的QR分解與約減的LLL算法結(jié)合,，其計算復(fù)雜度與LLL算法相比，每幀MIMO-OFDM信號節(jié)約844.8次列交換,。

　　H矩陣經(jīng)過排序QR分解,，將滿足如下表達式：

4 性能仿真分析

　　在2×2和4×4天線配置下，本節(jié)給出兩種檢測方案與ZF,、MMSE,、ML及LLL算法的性能比較,，如圖1、2所示,。OFDM信號的FFT長度為64,，循環(huán)前綴為16，調(diào)制方式為16-QAM,，信道編碼為卷積碼,。

　　從圖1和圖2知，天線配置為2×2時,，約減的LLL算法(SLR-MMSE)相對線性檢測,，性能提升較小。由于基矢量較少被約減,，它與排序QR分解結(jié)合檢測(SortedSLR-MMSE)的性能相對于LR-MMSE算法,在BER=10-3時,，信噪比損失約0.2 dB。約減LLL算法的性能提升隨天線數(shù)增加而增加,，在4×4天線配置時,，約減LLL算法與排序QR分解結(jié)合后,其性能優(yōu)于LLL-MMSE算法，在BER=10-3時,信噪比節(jié)省約0.2 dB,且復(fù)雜度降低更多,。                                      本文提出一種約減LLL算法與排序QR分解結(jié)合檢測,，其省去了LLL算法的列交換迭代，在保障誤碼性能的情況下,，減少了計算復(fù)雜度,，其性能提升隨天線數(shù)增加而增加。該算法未采用最優(yōu)的QR排序,，因此采用最優(yōu)排序分解以及與串行干擾相消、球形譯碼等非線性檢測結(jié)合亦可進一步研究,。

　　參考文獻

　　[1] 寧寧. 基于MIMO-OFDM系統(tǒng)的自適應(yīng)算法研究[J].微型機與應(yīng)用, 2011,30(2):62-64.

　　[2] 唐元元,張德民,劉哲哲,等.TD-LTE系統(tǒng)中軟輸出球形譯碼檢測算法研究[J]. 電子技術(shù)應(yīng)用, 2012,38(11):55-58.

　　[3] YAO H,， WORNELL G W. Lattice-reduction-aided detec-tors for MIMO communication systems[C]. IEEE GlobalTelecommunications Conference,2002(1):424-428.

　　[4] LENSTRA A K, LENSTRA H W, LOVSZ L. Factoringpolynomials with rational coefficients[J]. Mathematische An-nalen, 1982,261(4):515-534.

　　[5] WBBEN D, BHNKE R, KHN V, et al. MMSE-basedlattice-reduction for near-ML detection of MIMO systems[C].ITG Workshop on Smart Antennas,2004:106-113.

　　[6] GAN Y H, MOW W H. Multiple-input multiple-outputsignal detectors based on relaxed lattice reduction[P].UnitedStates, Patent Application Publication,13/348,469.2012-1-11.

　　[7] WEN Q, ZHOU Q, ZHAO C, et al. Fixed-point realiza-tion of lattice-reduction aided MIMO receivers with com-plex K-best algorithm[C]. 2013 IEEE International Con-ference on Acoustics, Speech and Signal Processing,2013:5031-5035.

　　[8] WBBEN D, BHNKE R, KHN V, et al. MMSE exten-sion of V-BLAST based on sorted QR decomposition[C].2003 IEEE 58th Vehicular Technology Conference,2003(1):508-512.