殷長濤,文志強(qiáng),胡駿飛
(智能信息感知及處理技術(shù)湖南省重點(diǎn)實(shí)驗(yàn)室, 湖南 株洲 412007)
摘要:基于分塊的壓縮感知算法適用于圖像信號(hào)的處理,通過平滑迭代閾值投影法可以快速重構(gòu)圖像,但存在低采樣率下重構(gòu)圖像質(zhì)量較差的缺點(diǎn)。基于全變差分的分塊壓縮感知算法,在一定程度上能提升重構(gòu)效果,但降低了運(yùn)算速度。針對(duì)以上算法的不足,提出基于多尺度的自適應(yīng)采樣圖像分塊壓縮感知算法。根據(jù)小波分解后不同層對(duì)重構(gòu)結(jié)果影響所占權(quán)重不同的特性,自適應(yīng)分配給每一層不同的采樣率,并在重構(gòu)時(shí)將平滑迭代閾值投影法應(yīng)用到每一層的每一個(gè)子帶的分塊上。實(shí)驗(yàn)結(jié)果表明,與傳統(tǒng)的迭代閾值投影法相比在重構(gòu)質(zhì)量上提高了1~3 dB,在重構(gòu)速度上與迭代閾值投影法相當(dāng)并優(yōu)于全變差分法。
關(guān)鍵詞:壓縮感知;多尺度;小波變換;自適應(yīng)采樣;圖像分塊
中圖分類號(hào):TP391文獻(xiàn)標(biāo)識(shí)碼:ADOI: 10.19358/j.issn.1674-7720.2016.24.013
引用格式:殷長濤,文志強(qiáng),胡駿飛. 基于多尺度的自適應(yīng)采樣圖像分塊壓縮感知算法[J].微型機(jī)與應(yīng)用,2016,35(24):42-45,49.
0引言
壓縮感知(Compresssive Sensing,CS)[1]最早是由DONOHO D等人提出的一種新的信號(hào)壓縮采樣方法。利用數(shù)據(jù)的冗余性,把原始信號(hào)通過觀測(cè)矩陣投影到低維空間,如果原始信號(hào)稀疏或是可壓縮的,則可以通過觀測(cè)值,利用凸優(yōu)化的方法很好地重構(gòu)出原始信號(hào)。
目前已有研究者將CS理論運(yùn)用于圖像數(shù)據(jù)的獲取,但是實(shí)踐中發(fā)現(xiàn),直接針對(duì)整幅圖像數(shù)據(jù)進(jìn)行壓縮感知時(shí)所需要的觀測(cè)矩陣會(huì)占用很大的存儲(chǔ)空間,重構(gòu)時(shí)運(yùn)算量過大,并且效果不理想。針對(duì)壓縮感知這個(gè)缺點(diǎn),GAN L等人提出了分塊壓縮感知(Block Compressed Sensing,BCS)[2]理論,該理論首先將圖像分割成相同大小的圖像塊,再對(duì)每一小塊分別進(jìn)行采樣重構(gòu)。MUN S等提出了分塊迭代閾值投影算法(BCSSPL)[3],該算法通過將BCS理論與Landweber迭代法[4]相結(jié)合,并且加入了維納濾波過程,在加快了重構(gòu)速度的同時(shí),也消除了分塊采樣所帶來的重構(gòu)結(jié)構(gòu)的快效應(yīng),很大程度上提高了分塊壓縮感知的可用性。蔡旭等人在文獻(xiàn)[3]的基礎(chǔ)上提出了基于全變差分自適應(yīng)采樣率分塊壓縮感知算法(TVBCSSPL)[5],根據(jù)圖像塊全變差分的值判斷其紋理復(fù)雜程度,進(jìn)而自適應(yīng)地分配采樣率。該算法在一定程度上提高了在低采樣率下的重構(gòu)精度,但算法比較復(fù)雜,需要較長的運(yùn)算時(shí)間。本文提出了一種改進(jìn)的基于多尺度采樣的分塊壓縮感知算法,并且利用基于光滑Landweber投影法作為重構(gòu)算法,通過實(shí)驗(yàn)證明提出的算法不僅可以保證大多數(shù)圖的重構(gòu)精度優(yōu)于分塊迭代閾值投影算法,而且重構(gòu)速度也優(yōu)于基于全變差分的自適應(yīng)采樣率分塊壓縮感知算法。
1相關(guān)理論
1.1分塊壓縮感知(BCS)
GAN L等人在文獻(xiàn)[2]中將基于分塊圖像的測(cè)量引入壓縮感知理論,以降低計(jì)算量和存儲(chǔ)器的負(fù)擔(dān)。假設(shè)要對(duì)一幅Ιρ×Ic大小的圖像進(jìn)行采樣,圖像的總像素?cái)?shù)用N=Ir×IC來表示。上分塊壓縮感知算法將圖像分成了很多B×B大小的圖像塊,并對(duì)這些小塊進(jìn)行相同的采樣操作。令Xi代表第i個(gè)圖像塊像素值所組成的向量,則對(duì)應(yīng)的采樣值為:
![@}TL]}9DYAS_9TAL7Z20Q4R.png @}TL]}9DYAS_9TAL7Z20Q4R.png](http://files.chinaaet.com/images/2017/02/16/6362287050389512219766754.png)
由于Φ是一個(gè)對(duì)角矩陣,因此只需要存儲(chǔ)大小為nB×B2的ΦB,而不是存儲(chǔ)大小為n×N的矩陣,減輕了存儲(chǔ)器的負(fù)擔(dān),增加了算法的實(shí)時(shí)性。
1.2基于Landweber投影的重構(gòu)方法(SPL)
FOWLER J E等人在2009年提出了基于Landweber投影的塊壓縮感知重構(gòu)算法。算法將解決數(shù)學(xué)上反問題的Landweber迭代法[4]應(yīng)用于圖像重構(gòu)過程中,提高了算法效率和重構(gòu)的精度。算法步驟如下:
(1)如式(1)所示分塊采樣后,分別得到了各個(gè)圖像塊的采樣值,將第i個(gè)圖像塊的采樣值記為yi,并假設(shè)重構(gòu)圖像X(k)=Φ-1Y,令迭代次數(shù)k=0。
(2)對(duì)第k次迭代重構(gòu)的圖像進(jìn)行維納濾波,X(k)=Wienner(X(k))
(3)將第k次迭代得到的第j個(gè)圖像塊xj(k)依次執(zhí)行下式:
(j)(k)=(k)j+ΦTB(y(k)j-ΦBx(k)j)(3)
(4)將第k次迭代得到的重構(gòu)圖像(k)投影到Ψ域,得到(k)=Ψ(k),該矩陣為稀疏矩陣,并對(duì)(k)做閾值處理。
(5)將(k)作ΨT(k)變換得到時(shí)域中重構(gòu)圖像(k),并對(duì)重構(gòu)圖像塊(k)j執(zhí)行下式:
X(k+1)j=(k)j+ΦTB(y(k)j-ΦB(k)j)(4)
(6)若兩次迭代返回的均方根誤差之差小于0.000 1,則終止迭代,否則返回步驟(2)繼續(xù)迭代。
由于該算法對(duì)圖像進(jìn)行了較多的平滑處理,因此導(dǎo)致圖像細(xì)節(jié)變得模糊,這種現(xiàn)象在采樣率低的情況下十分明顯。
1.3基于全變差分的自適應(yīng)采樣率分塊壓縮感知(TV-BCS-PL)
針對(duì)以上算法的不足,蔡旭等人提出了基于全變差分自適應(yīng)采樣率分塊壓縮感知[5],該算法根據(jù)圖像塊的全變差分值來度量其紋理的復(fù)雜程度,并根據(jù)不同的全變差分值對(duì)采樣率進(jìn)行自適應(yīng)分配。具體算法如下。
假定原圖像大小為M×N,分塊圖像大小為B×B,則整個(gè)圖像中有num=M×N/B2個(gè)圖像塊,用I來表示整幅圖像,K表示當(dāng)前子塊,并用(s,t)坐標(biāo)表示圖像塊在圖像中的位置,Kij代表圖像塊中的每個(gè)像素,初始采樣率為R,則圖像塊K的全差分值為:
TVl1l2=∑DhK2+Dv K2(5)
式中DhK代表水平方向的前像素與后像素的差值,DvK代表下方像素與本像素的差值,并且將整幅圖像分為四部分,每部分的DhK和DvK的計(jì)算方法如圖1所示。

(1)第一部分圖像塊為1≤s<M/B且1≤t<N/B的塊:
![N)]W)6%DC@5MD18WL%F5Q]6.png N)]W)6%DC@5MD18WL%F5Q]6.png](http://files.chinaaet.com/images/2017/02/16/6362287057697812216868808.png)
根據(jù)式(6)計(jì)算出每個(gè)圖像塊的TV值,并利用下式自適應(yīng)分配對(duì)各塊的采樣率:
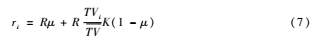
其中μ為采樣率控制因子,文獻(xiàn)[5]中將其設(shè)為0.35,代表根據(jù)TV值分配采樣率的權(quán)重占總采樣率的35%。為了防止過采樣或欠采樣,對(duì)ri值進(jìn)行閾值處理:
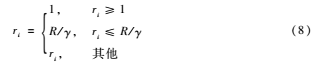
文獻(xiàn)[5]中取γ為1.9用來控制最小采樣率,并且為了保證總采樣數(shù)保持不變,令K=R/ri,對(duì)采樣率的分配進(jìn)行多次迭代直到|K-1|<0.001,跳出迭代后得到的ri就是每個(gè)子塊對(duì)應(yīng)的采樣率。
2基于多尺度自適應(yīng)采樣的塊壓縮感知算法
2.1多尺度自適應(yīng)采樣
對(duì)于基于平滑投影的多尺度分塊壓縮感知來說,采樣算子A分為兩部分,第一部分是多尺度變換Ω(例如離散小波變換等)和多尺度分塊觀測(cè)矩陣Φ′,所以A=Φ′Ω,于是可以通過下式對(duì)整幅圖像采樣:
y=Φ′Ωx(9)
假設(shè)Ω對(duì)圖像進(jìn)行了L層小波分解,因此Φ′是L個(gè)不同的基于塊的采樣算子分別與L層中每一層小波分解對(duì)應(yīng)。x的小波變換可表示為:
=Ωx(10)
的第l層小波分解中子帶s被分割為Bl×Bl的小塊,并用一個(gè)與之大小對(duì)應(yīng)的Φ觀測(cè)矩陣對(duì)其采樣。假設(shè)用l,s,j表示小波分解中第l層的子帶s中的第j個(gè)子塊,那么采樣過程可以用下式表示:
yl,s,j=Φll,s,j(11)
其中1≤l≤L。
對(duì)圖像采樣過程中的采樣率進(jìn)行了自適應(yīng)分配。對(duì)低頻部分進(jìn)行全部采樣,即s0=1,對(duì)于其他層的采樣率可用sl表示并可由(12)式求出:
Sl=WlS′(12)
由此可得圖像總采樣率為:

通過將總采樣率S和小波分解每層所占比重wl帶入式(13)求出S′,通過S′可以求出每層分配到的采樣率。然而求出的采樣率有可能有一個(gè)或多個(gè)Sl>1,因此需調(diào)整算法使得對(duì)于所有的Sl都必須符合Sl≤1。具體做法是,假設(shè)Sl>1,則令Sl=1,相應(yīng)的(13)式需要調(diào)整為:
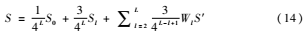
再根據(jù)式(14)求出其他層采樣率,如果求出的結(jié)果中依然有Sl>1則可以重新迭代上述過程,直至所有Sl都小于等于1。通過實(shí)驗(yàn)對(duì)比發(fā)現(xiàn)對(duì)于每層所占比重采用式(15)得出的結(jié)果最好:
Wl=16L-l+1(15)
2.2多尺度重構(gòu)
多尺度重構(gòu)采用的重構(gòu)算法包括對(duì)于整幅圖像利用維納濾波器進(jìn)行平滑的過程和為達(dá)到圖像更加稀疏的效果將整幅圖像映射到稀疏域的閾值化處理過程。在這兩個(gè)操作之間是Landweber迭代過程,用x←x+ΦT(y-Φx)來表示,其中Φ是觀測(cè)矩陣,下面的偽代碼描述了如何將多尺度變換加入基于平滑投影的Landweber算法中。
function =MultiScale-BCS (y,{Φl,1≤l≤L},Ψ,Ω)
forl++ (1≤l≤L)
fors++ (s∈{H,V,D})
for j++
(0)l,s,j=ΦTlyl,s,j
endfor
endfor
endfor
k=0
do
x(k)=Ω-1(k)
(k)=Wiener(x(k))
^k=Ω(k)
forl++ (1≤l≤L)
fors++(s∈{H,V,D})
for j++
^^(k)l,s,j=^(k)l,s,j+ΦTl(yl,s,j-Φl^(k)l,s,j)
x︶︶(k)=ΨΩ-1^^(k)
x︶(k)=Threshold(x︶︶(k))
(k)=ΩΨ-1x︶(k)
endfor
endfor
endfor
forl++ (1≤l≤L)
fors++ (s∈{H,V,D})
for j++
endfor
endfor
endfor
(k)l,s,j=(k)l,s,j+ΦTl(yl,s,j-Φl(k)l,s,j)
D(k+1)=(k+1)-^^(k)2
k=k+1
enddo
While(|D(k)-D(k-1)|>10-2)
=(k)
endwhile
3實(shí)驗(yàn)結(jié)果與比較
3.1實(shí)驗(yàn)環(huán)境
實(shí)驗(yàn)平臺(tái)是搭載了雙核2.3 GHz CPU和4 GB內(nèi)存的筆記本電腦,實(shí)驗(yàn)環(huán)境為Windows 7操作系統(tǒng),并在MATLAB 2014a上運(yùn)行。算法使用了小波工具箱和l1magic工具箱。
3.2實(shí)驗(yàn)結(jié)果
采用三張大小為512×512的圖像處理領(lǐng)域常用灰度圖像來驗(yàn)證所提出算法的性能。實(shí)驗(yàn)將提出的算法分別對(duì)比三種算法在不同采樣率下重構(gòu)圖像的質(zhì)量(PSNR),對(duì)比算法包括基于平滑投影迭代分塊壓縮感知算法(BCSSPL)[6]、基于全變差分的壓縮感知算法(TV)[7]以及一個(gè)多尺度變換的衍生算法GPSR[8]。所提出算法與BCSSPL算法均采用雙樹離散小波變換作為稀疏變換。其中本文算法采用3層離散小波變換,并采用9/7雙正交小波[9]作為采樣域的變換。對(duì)于小波變換的第l層,每個(gè)大小為B×B的分塊被分別采樣。實(shí)驗(yàn)采用分塊大小為16、32以及64,分別對(duì)應(yīng)層為l=1,2,3。傳統(tǒng)的BCSSPL算法和TV算法采用分塊大小為32。
表1、表2和表3分別是在三種不同圖像下的重構(gòu)效果比較。通過以上實(shí)驗(yàn)結(jié)果可以看出,在多數(shù)情況下與傳統(tǒng)的BCSSPL相比,本文提出的算法重構(gòu)結(jié)果的峰值信噪比要高出1~3 dB,并且在低采樣率時(shí)提出算法相對(duì)于TV算法有1~2 dB的性能提升。
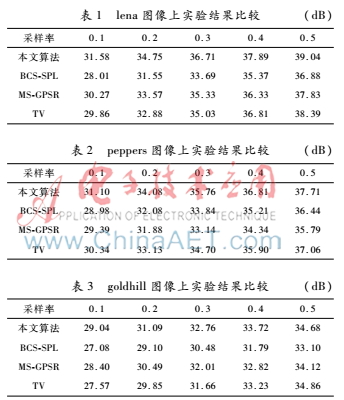
表4是當(dāng)采樣率為0.3時(shí)對(duì)lena圖的重構(gòu)時(shí)間比較。根據(jù)表4可知,本文提出的算法比BCSSPL快了17 s,而MSGPSR和TV兩種算法則相當(dāng)耗時(shí)。其中TV算法盡管采用了快速SRM采樣算子,依然將近要用2個(gè)小時(shí)才可以完成對(duì)圖像的重建。

4總結(jié)
本文將多尺度分解應(yīng)用于平滑投影的Landweber分塊壓縮感知算法并在小波域進(jìn)行采樣。提出的重構(gòu)算法是將BCSSPL算法應(yīng)用到小波分解后對(duì)每一層上每個(gè)子帶的分塊再分別重構(gòu)每一個(gè)分塊。實(shí)驗(yàn)結(jié)果顯示,在重構(gòu)效果的對(duì)比上,提出的算法比原始BCSSLP算法在時(shí)域上進(jìn)行采樣和重構(gòu)時(shí),重構(gòu)質(zhì)量普遍要高1~3 db。由此得出,提出的算法在提高圖像重構(gòu)效果的同時(shí),依舊保持了BCSSPL算法的運(yùn)算速度。基于分塊的壓縮感知算法的優(yōu)點(diǎn)在于降低了采樣和重構(gòu)算法的計(jì)算復(fù)雜度,同時(shí)提高了算法的實(shí)時(shí)性。提出的算法在小波域?qū)D像進(jìn)行分塊的采樣和重構(gòu),雖然保留了BCS算法的優(yōu)點(diǎn),但是在對(duì)小波分解的觀測(cè)過程中,A=Φ′Ω,小波變換破壞了觀測(cè)矩陣Φ′分塊對(duì)角的結(jié)構(gòu)特性,產(chǎn)生了一個(gè)稠密的A矩陣,這就給壓縮感知在硬件實(shí)現(xiàn)上帶來了很大的挑戰(zhàn)。因此,提出算法在提升重構(gòu)效果的同時(shí),也帶了算法硬件實(shí)現(xiàn)上的挑戰(zhàn),如何解決觀測(cè)矩陣結(jié)構(gòu)問題是之后工作的重點(diǎn)。
參考文獻(xiàn)
[1] DONOHO D. Compressed sensing [J] . IEEE Transactions on Information Theory, 2006,52(4):1289 1306.
[2] GAN L. Block compressed sensing of natural images [C]. 2007 15th International Conference on Digital Signal Processing,IEEE,2007:403 406.
[3] MUN S, FOWLER J E . Block compressed sensing of natural images[C]. 2009 16th IEEE International Conference on Image Processing (ICIP),IEEE,2009:30213024.
[4] 王兵賢, 胡康秀, 王澤文. 反問題的Landweber迭代法及其應(yīng)用研究進(jìn)展[J]. 計(jì)算機(jī)應(yīng)用研究, 2013, 30(9):25832586.
[5] 蔡旭, 謝正光, 黃宏偉,等. 一種自適應(yīng)低采樣率圖像分塊壓縮感知算法[J]. 小型微型計(jì)算機(jī)系統(tǒng), 2016,37(3):612 616.
[6] MUN S, FOWLER J E. Block compressed sensing of images using directional transforms[C]. IEEE International Conference on Image Processing, 2009:3021 3024.
[7] CANDS E J, ROMBERG J K, TAO T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure & Applied Mathematics, 2005, 19(5):410 412.

