0 引言

    永磁同步電機(jī)由于其體積小,、結(jié)構(gòu)簡單、慣性小和效率高等優(yōu)點,，得到廣泛關(guān)注,，成為當(dāng)今電機(jī)控制領(lǐng)域的一個研究重點，同時人們對其控制要求也越來越高,，提出了少傳感器甚至無傳感器的研究思想,。近年來，較為普遍的是電機(jī)無位置傳感器的控制方式,，但是在電機(jī)定位精度要求較高的場合,，位置傳感器則必不可少。因此,，從動態(tài)性能,、開發(fā)成本等角度來考慮，無電流傳感器的控制方式^[1-2]也逐漸成為研究熱點,。

    電機(jī)的無電流傳感器控制方式意味著無電流環(huán)控制,，也就放棄了控制器快速響應(yīng)的特性,，在此，我們提出一種虛擬電流環(huán)控制的概念,，以滿足對控制器電流的反饋控制,。

    本文以永磁同步電機(jī)-虛擬電流環(huán)控制方案為研究對象，并基于該方案進(jìn)行仿真和實驗,，結(jié)果表明該方案可行,，實用價值較高。 

1 PMSM在d-q坐標(biāo)系中的數(shù)學(xué)模型及常規(guī)矢量控制分析

1.1 PMSM在d-q坐標(biāo)系中的數(shù)學(xué)模型

    在PMSM轉(zhuǎn)子無阻尼繞組的情況下,，忽略溫度,、磁滯損耗及渦流對電機(jī)的影響，在d-q坐標(biāo)系中,，永磁同步電機(jī)電壓,、磁鏈及轉(zhuǎn)矩的數(shù)學(xué)模型^[3]如下。

    電壓方程：

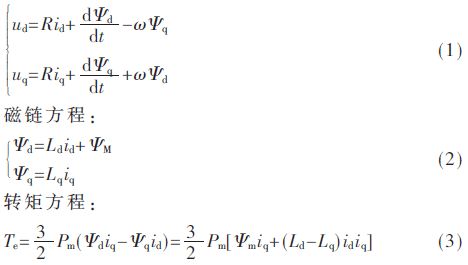
    式中,，u_d,、u_q為電機(jī)定子分別在d、q兩軸的電壓分量,；R為電機(jī)定子電阻,； i_d、i_q為電機(jī)定子分別在d,、q兩軸的電流分量,；Ψ_d、Ψ_q為電機(jī)定子分別在d,、q兩軸的磁鏈分量,；ω為電機(jī)轉(zhuǎn)子轉(zhuǎn)速；L_d,、L_q為電機(jī)分別在d,、q兩軸的電感分量；Ψ_M為電機(jī)永磁體磁鏈,；T_e為電機(jī)轉(zhuǎn)矩,；P_m為電機(jī)極對數(shù)。

1.2 常規(guī)矢量閉環(huán)控制系統(tǒng)

    對于非隱極式PMSM,，電機(jī)在d,、q兩軸的電感分量不相等，即L_d≠L_q,；對于隱極式PMSM，電機(jī)在d,、q兩軸的電感分量相等,，即L_d=L_q,，從式(3)中可以看出，電機(jī)的電磁轉(zhuǎn)矩T_e只與交軸電流i_q相關(guān),，因此在設(shè)計控制參數(shù)時,，一般取i_d=0。

    本文以隱極式PMSM為例,，即i_d=0來分析控制方案,，如圖1所示。

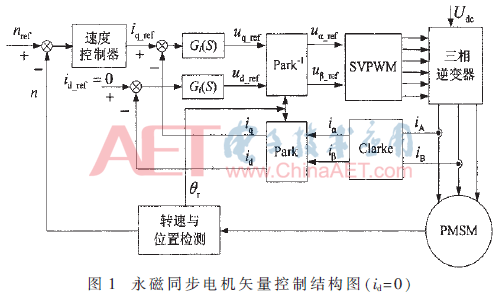
    該控制系統(tǒng)由雙閉環(huán)控制構(gòu)成,。外環(huán)是轉(zhuǎn)子轉(zhuǎn)速的閉環(huán)控制,，內(nèi)環(huán)為定子在d、q軸電流分量 i_d和i_q的閉環(huán)控制,。外環(huán)中,，轉(zhuǎn)子的實際轉(zhuǎn)速n由位置傳感器實時檢測并計算得到，與給定轉(zhuǎn)速n_ref進(jìn)行比較后,，通過速度控制器實現(xiàn)電機(jī)的速度調(diào)節(jié),，其輸出值i_{q_ref}作為內(nèi)環(huán)中i_q的參考值；內(nèi)環(huán)中,，定子在d,、q軸實際電流分量為 i_d和 i_q，由電流傳感器測取后經(jīng)Clarke-Park變換得到,，繼而分別與兩者的參考值i_{d_ref}(為零)和i_{q_ref}相比較,，并通過電流控制器實現(xiàn)對電機(jī)電流的控制，最后兩者的調(diào)節(jié)結(jié)果經(jīng)過Park^-1變換后輸入至SVPWM模塊進(jìn)行調(diào)制,，輸出6路PWM驅(qū)動信號,，用于控制PMSM的驅(qū)動電壓的大小，由此實現(xiàn)其轉(zhuǎn)速,、電流的雙閉環(huán)控制^[4-6],。

2 虛擬電流環(huán)控制策略分析

    無電流傳感器，則PMSM控制系統(tǒng)無法對電流進(jìn)行檢測反饋,。因此,，虛擬電流環(huán)控制策略的關(guān)鍵是如何構(gòu)造電流反饋^[7-8]。

    由PMSM的磁鏈方程帶入到電壓方程,，即式(2)帶入式(1),，可得：

    由式(4)明顯可知，PMSM定子d,、q軸電流i_d,、i_q可由電機(jī)轉(zhuǎn)子速度ω和定子d、q軸電壓u_d、u_q來估算,。PMSM驅(qū)動電壓是由直流電壓逆變后提供的,，為PWM脈沖波，直接測取難度較大,，因此一般不直接對電機(jī)的線電壓進(jìn)行測取,，而是根據(jù)直流母線電壓和SVPWM調(diào)制模塊的輸入d、q軸電壓給定值來推算出電機(jī)實際的電壓,。

    對式(4)進(jìn)行拉普拉斯變換得到i_d,、i_q的估算方程，如下所示：

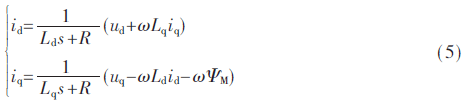
    由于式(5)涉及一階微分方程,，計算難度較大,。為了便于實現(xiàn)數(shù)字化并對系統(tǒng)進(jìn)行仿真，對i_d,、i_q的估算方程進(jìn)行離散化處理,，如下所示：    

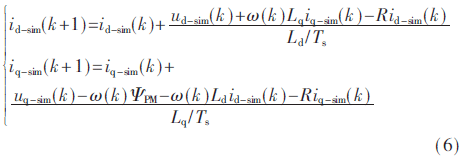
    由離散化的電流估算公式(6)可以看出，電機(jī)參數(shù)對其控制性能的影響較大,。因此需要提高電機(jī)的穩(wěn)定性能,；同時，由電機(jī)的電壓方程式(1)可知,，電流PI調(diào)節(jié)器的輸出結(jié)果只考慮到d,、q軸電流分別對d、q軸電壓的影響,，而忽略了它們之間的耦合,。綜合以上兩個方面，為提高系統(tǒng)控制的穩(wěn)定性能以及補(bǔ)償d,、q軸電流對電壓的影響,，本文對電動勢進(jìn)行了補(bǔ)償，即：

    將離散化電流估算公式(6)和電動勢補(bǔ)償公式(7)融入到常規(guī)矢量控制方案中,，可構(gòu)建虛擬電流環(huán)控制結(jié)構(gòu),，如圖2所示。

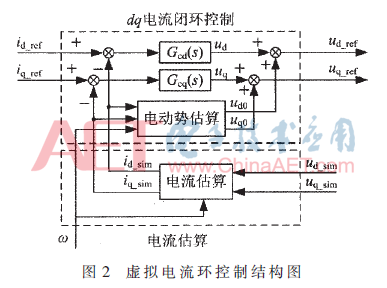
3 系統(tǒng)仿真模型的建立

    在分析PMSM虛擬電流環(huán)控制的基礎(chǔ)上,，本文采用MATLAB/Simulink搭建了虛擬電流環(huán)控制仿真模塊,，如圖3所示。

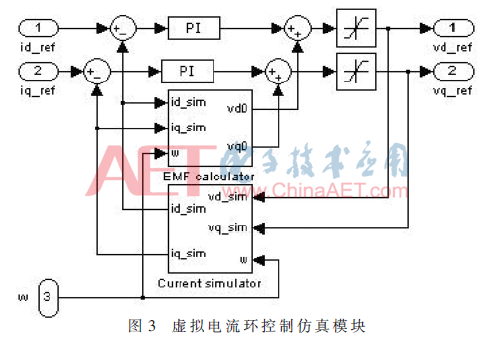
    其中,，電流估算仿真模塊如圖4所示,。

    在以上分析的基礎(chǔ)上，文章搭建了永磁同步電機(jī)—虛擬電流環(huán)控制系統(tǒng)仿真模型,，如圖5所示,。

4 仿真結(jié)果分析

    為了驗證上述提出的虛擬電流環(huán)對系統(tǒng)控制的可靠性,，現(xiàn)對搭建的系統(tǒng)仿真模型進(jìn)行仿真分析，參數(shù)設(shè)置如下：R=2.08 Ω,；Ψ_M=0.107 Wb,；L_d=L_q=8.2×10^-3 H；J=0.32×10^-3 kg·m²,；極對數(shù)P_n=4；摩擦系數(shù)為B=3×10^-4 N·m·s,；額定轉(zhuǎn)速為n_ref=3 000 r/min,，逆變器開關(guān)頻率為10 kHz，單相電源供電,。

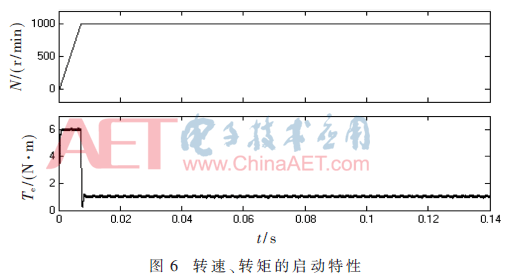
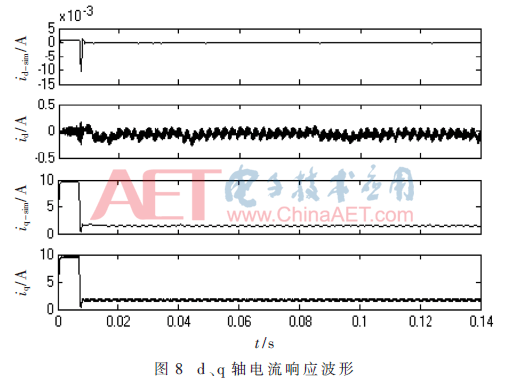
    圖6~圖8為電機(jī)負(fù)載轉(zhuǎn)矩為1 N·m,、給定轉(zhuǎn)速為1 000 r/min時各變量的仿真波形。其中,，電機(jī)轉(zhuǎn)速,、轉(zhuǎn)矩相應(yīng)波形如圖6 所示，可以看出電機(jī)啟動時間約為7 ms,，轉(zhuǎn)速響應(yīng)快,，跟隨性好，轉(zhuǎn)矩波形基本穩(wěn)定,。繞組三相電流響應(yīng)波形如圖7所示,，波形平滑穩(wěn)定。d,、q軸電流響應(yīng)波形如圖8所示,，電機(jī)啟動穩(wěn)定后，d軸估算電流id-sim大小基本穩(wěn)定在0值,，實際電流id波形在0值上下小幅脈動,，q軸估算電流i_q-sim與實際電流i_q兩者波形基本相同。 

    為驗證該控制系統(tǒng)在負(fù)載或轉(zhuǎn)矩發(fā)生突變時的響應(yīng)性能,，作如下處理：電機(jī)在啟動后的0.05 s處電機(jī)的給定轉(zhuǎn)速由原來的1 000 r/min瞬間增至2 000 r/min,，在0.1 s處，電機(jī)負(fù)載由原來的1 N·m瞬間增至4 N·m,。

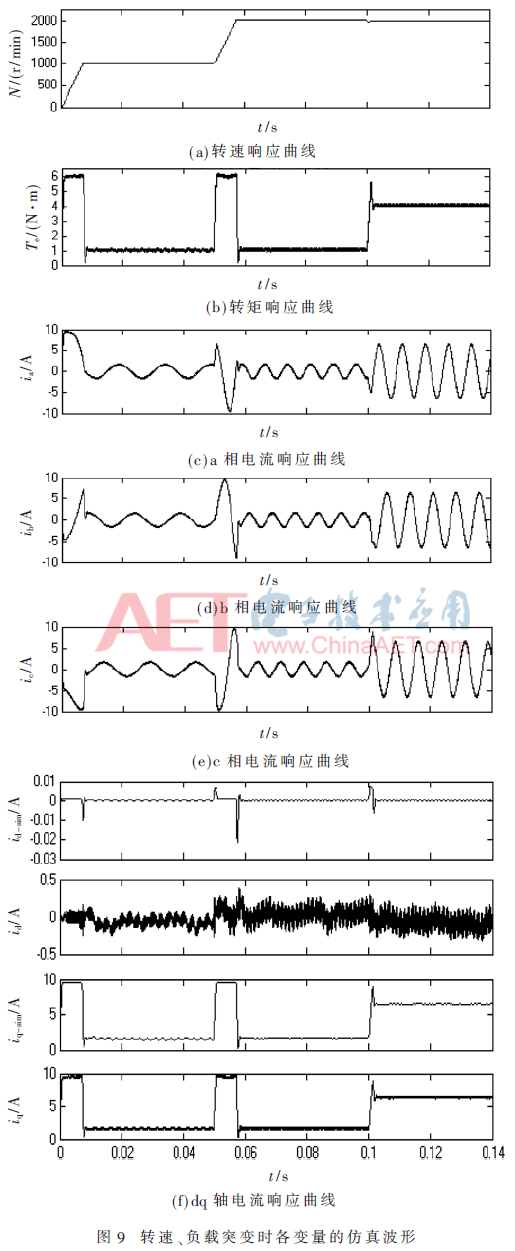
    系統(tǒng)中各變量的仿真波形如圖9所示,。在0.05 s處，給定轉(zhuǎn)速突變,，轉(zhuǎn)速響應(yīng)波形如圖9(a)所示,，能夠快速跟隨給定值快速變化。轉(zhuǎn)矩如圖 9(b)所示,，波形小幅振動后又迅速恢復(fù)原值,。三相定子繞組電流如圖9(c)~(e)所示，波形快速調(diào)整后，幅值不變,，頻率變大,；在0.1 s處，電機(jī)負(fù)載突變,，如圖所示,，轉(zhuǎn)速幾乎不受影響，轉(zhuǎn)矩快速增大為4 N·m后保持不變,，三相繞組電流頻率不變,，幅值變大。

    圖9(f)為d,、q軸電流仿真波形,，可以看出，在電機(jī)啟動并穩(wěn)定后,，d軸估算電流i_d-sim基本上穩(wěn)定在0值不變,，而其實際電流i_d則在0值上下小幅波動。q軸估算電流i_q-sim和實際電流i_q與轉(zhuǎn)矩的仿真波形基本相似,。

    從以上結(jié)果可以看出,，電機(jī)能夠快速并穩(wěn)定啟動，在負(fù)載或轉(zhuǎn)矩發(fā)生突變時,，轉(zhuǎn)速能較快跟隨,，轉(zhuǎn)矩能平穩(wěn)響應(yīng)，仿真系統(tǒng)的電流估算模塊也能夠較準(zhǔn)確地估算出電機(jī)實際電流,，且d軸實際電流基本上保持在0值左右,，基本上實現(xiàn)了i_d=0的矢量控制。由此驗證,，在電機(jī)沒有電流傳感器的情況下,，虛擬電流環(huán)控制策略可實現(xiàn)對電機(jī)電流的反饋控制。

5 實驗結(jié)果分析

    為了更進(jìn)一步驗證虛擬電流環(huán)控制策略的可行性,，在以上仿真的基礎(chǔ)上搭建了實驗平臺,，并對實驗結(jié)果進(jìn)行了分析。

    如圖10所示為轉(zhuǎn)速為300 r/min和轉(zhuǎn)矩為1 N·m時,，定子繞組A相實際采樣電流波形與其估算電流波形,，明顯可以看出估算電流與實際電流值較接近；圖11為電機(jī)給定轉(zhuǎn)速在400 r/min時定子繞組A,、B相的空載估算電流波形,，它們由估算的交、直軸電流即i_d-sim和i_q-sim經(jīng)Park^-1變換所得,，可以看出估算電流正弦度較好,，相序?qū)ΨQ,；圖12為電機(jī)A相給定電壓和定子繞組A相估算電流波形，可以看出電機(jī)給定相電壓波形近似呈馬鞍波狀,；圖13~圖15為電機(jī)空載的情況下,，給定轉(zhuǎn)速由200 r/min突增至400 r/min時，電機(jī)轉(zhuǎn)速,、A相和B相估算電流以及d,、q軸估算電流的響應(yīng)波形?？煽闯鲭姍C(jī)轉(zhuǎn)速迅速跟隨給定轉(zhuǎn)速變化,，響應(yīng)時間約為55 ms。A相和B相估算電流的正弦波形幅值不變,、頻率變大。q軸估算電流在給定轉(zhuǎn)速突增時瞬時加大,，當(dāng)轉(zhuǎn)速重新穩(wěn)定后,，又恢復(fù)為原值并保持不變。d軸估算電流雖有小幅波動,，但又很快又穩(wěn)定在0值不變,。

6 結(jié)論

    本文從永磁同步電動機(jī)在無電流傳感器的情況下出發(fā)，提出采用虛擬電流環(huán)控制策略實現(xiàn)電流反饋,。由仿真和實驗結(jié)果分析可知,，控制系統(tǒng)采用該方案后具有響應(yīng)速度快、控制精度高等良好的控制性能,。驗證了方案的設(shè)計是可行的,，具有一定實用價值。

參考文獻(xiàn)

[1] 周雅夫,，沈曉勇,，連靜，等．車用驅(qū)動電機(jī)無電流傳感器控制[J]．吉林大學(xué)學(xué)報：工學(xué)版,，2012,，42(1)：28-32．

[2] 黃偉鈿，陳建賓．無電流環(huán)的PMSM控制系統(tǒng)仿真與實驗研究[J]．微計算機(jī)信息,，2010,，26(10)：168-212．

[3] 孫丹．高性能永磁同步電動機(jī)直接轉(zhuǎn)矩控制[D]．杭州：浙江大學(xué)，2004：132-133.

[4] 田亞菲,，何繼愛．電壓空間矢量脈寬調(diào)制(SVPWM)算法仿真實現(xiàn)及分析[J]．電力系統(tǒng)及其自動化學(xué)報,，2004(4)：68-71．

[5] 崔硼，王楠．基于DSP的交流永磁同步電動機(jī)伺服系統(tǒng)及其智能控制研究[D]．天津：天津大學(xué),，2002：10-13．

[6] 朱小鷗,，馮曉云．永磁同步電機(jī)直接轉(zhuǎn)矩控制系統(tǒng)研究與仿真[J]．機(jī)車電傳動,，2005(3)：16-19．

[7] RAUTE R，CARUANA C,，STAINES C．A review of sensor-less control in induction machines using HF injection,，test vectors and PWM harmonics[C]．2011 IEEE Symposium on Sensorless Control for Electrical Drives，2011：47-55．

[8] RAMAKRISHNAN R,，RAKIB I．Real time estimation of parameters for controlling and monitoring permanent magnet synchronous motors[C]．2009 IEEE International Electric Machines and Drives Conference(IEMDC'09),，2009：1194-1199．

作者信息:

申  娟1，周  實2

（1．國網(wǎng)上海市電力公司電力科學(xué)研究院,，上海200051,；2.上海電氣集團(tuán)股份有限公司中央研究院，上海200070）