0 引言

    甲狀腺結(jié)節(jié)一直以來都是一個非常普遍的醫(yī)學(xué)問題,，研究表明全球大約有50%的人都有甲狀腺結(jié)節(jié)^[1],。因此對甲狀腺結(jié)節(jié)的病理特征研究就顯得特別重要，而在此之前對結(jié)節(jié)所在區(qū)域進(jìn)行精確的分割就成為了當(dāng)前的首要任務(wù),。圖像分割在數(shù)字圖像處理領(lǐng)域中處于很重要的地位,，國內(nèi)外學(xué)者對此作了廣泛研究。文獻(xiàn)[2]提出的CV(Chan Vese)模型就是一種常用的分割模型,。該模型利用圖像全局信息能有效克服斑點(diǎn)噪聲和干擾,，并且能很好地處理模糊邊緣，抗噪性強(qiáng),，但對灰度不均勻的圖像分割效果差,；MUMFORD D^[3]等人對該算法進(jìn)行改進(jìn)提出了PS(Piecewise Smooth)模型。雖然該模型克服了CV模型的缺點(diǎn),，但計算量過大,；Li Chunming^[4]等人在CV模型的基礎(chǔ)上提出了LBF(Local Binary Fitting)模型。該模型引入高斯函數(shù)構(gòu)造兩個圖像的局部擬合函數(shù),，能有效獲取圖像的局部灰度信息,，并用它們替代CV模型中兩個全局?jǐn)M合函數(shù)，實(shí)現(xiàn)了對大部分灰度不均勻圖像的分割,，但由于其在演化過程中多次使用卷積,，因此計算量大，而且必須選擇合適的初始輪廓位置才能獲得精確的分割結(jié)果,； ZHANG K H^[5]等人在LBF模型的基礎(chǔ)上提出了LIF(Local Image Fitting)模型,，該模型對灰度不均勻圖像分割時不僅能取得較理想的分割效果，而且與LBF模型相比迭代次數(shù)明顯降低,，因此分割效率大大提高,。但LIF模型僅在分割效率和參量設(shè)置上作了改進(jìn)，對初始輪廓的選取依舊敏感,。

    文獻(xiàn)[6]指出,，圖像的灰度值不能簡單地用一種分布來描述，不同點(diǎn)的灰度均勻性不同,，因此僅用一個固定的模型來計算不同區(qū)域的灰度統(tǒng)計信息是不準(zhǔn)確的,。因此，本文提出了一種新的水平集活動輪廓模型來分割甲狀腺結(jié)節(jié)圖像,。首先在經(jīng)典的LIF模型中加入局部梯度信息,，構(gòu)造了既包含有灰度信息也包含有梯度信息的GLIF(Gradient Local Image Fitting)模型，并以此構(gòu)造局部擬合能量項,。然后再用經(jīng)典的CV模型構(gòu)造全局能量函數(shù),。最后將兩種能量結(jié)合起來，使得水平集函數(shù)在局部能量和全局能量的共同支配下朝著目標(biāo)的真實(shí)邊界演化,。 實(shí)驗結(jié)果表明,，本文模型不僅能準(zhǔn)確分割具有低對比度、弱邊緣,、強(qiáng)噪聲,、灰度不均勻等特點(diǎn)的圖像，而且對初始輪廓的敏感性也有所降低,。

1 相關(guān)模型描述

1.1 CV模型

    CHAN T F和VESE L提出的CV模型^[2],，其基本思想是把圖像分為背景區(qū)域和目標(biāo)區(qū)域兩部分，并且假設(shè)這兩個部分的灰度值都各自是均勻的,。對于圖像區(qū)域內(nèi)任一閉合曲線C,，c₁和c₂分別用來表示曲線C內(nèi)部和外部的灰度均值，則CV模型能量泛函的水平集形式如下所示：

    CV模型較傳統(tǒng)的活動輪廓模型有了較大的改進(jìn),，它無需計算圖像梯度,，并且綜合利用了圖像的全局信息，因此對大部分的圖像都能實(shí)現(xiàn)準(zhǔn)確的分割,。但對灰度不均勻圖像,，例如甲狀腺結(jié)節(jié)超聲圖像，該算法無法對其進(jìn)行精確的分割,。

1.2 LIF模型

    ZHANG K H^[5]等人利用圖像的局部灰度統(tǒng)計信息來構(gòu)造圖像局部擬合函數(shù),，從而提出了LIF模型。對于圖像中任一點(diǎn)x∈Ω,，LIF模型的能量泛函定義為如下形式：

其中,，m₁、m₂表示的是由高斯窗函數(shù)決定的局部灰度均值,。LIF模型雖然可以實(shí)現(xiàn)對灰度不均勻圖像的分割,，但其對初始輪廓位置的選取比較苛刻，只有當(dāng)初始輪廓位置選取合適時才能取得精確的分割結(jié)果,。

2 本文提出的模型

2.1 改進(jìn)的LIF模型

    傳統(tǒng)的LIF模型僅單一地利用圖像的局部灰度信息來分割灰度不均勻圖像,，當(dāng)圖像受噪聲污染嚴(yán)重時可能無法獲得令人滿意的分割結(jié)果，且演化時水平集函數(shù)極易面臨局部最優(yōu),。而引入圖像的梯度信息可以去除圖像上相當(dāng)部分的局部極小值和噪聲,，因此對傳統(tǒng)的LIF模型進(jìn)行改進(jìn)，引入圖像的局部梯度信息,，利用兩種局部統(tǒng)計信息構(gòu)造新的局部能量擬合模型稱之為GLIF模型,。該新模型由于多用了一個局部梯度信息，可以更好地約束水平集能量泛函的收斂,，因此也就在很大程度上避免了傳統(tǒng)LIF模型容易出現(xiàn)局部極小的問題,。對于任一點(diǎn),，(x∈Ω)該新模型的水平集形式能量泛函表示如下：

    GLIF模型利用圖像局部灰度統(tǒng)計信息和局部梯度信息克服了演化過程中易陷入局部極小值的缺點(diǎn)，但其對初始輪廓的位置依然比較敏感,。為了解決這一問題,，本文提出了結(jié)合CV模型全局性優(yōu)點(diǎn)的方法。

2.2 融合全局與局部的CV-GLIF模型

    考慮到甲狀腺結(jié)節(jié)超聲圖像往往呈現(xiàn)明顯的灰度不均勻,，而且結(jié)節(jié)區(qū)域邊界通常比較模糊,，所以單單利用GLIF模型或CV模型都不可能完成對結(jié)節(jié)區(qū)域的精確分割。為了實(shí)現(xiàn)對甲狀腺結(jié)節(jié)的有效分割,，提出了GLIF模型和CV模型相結(jié)合的算法,，集成了兩種模型各自的優(yōu)點(diǎn)。其能量泛函的水平集形式表示如下：

    式(13)中等號右邊第一項表示的是全局能量項,，由CV模型的全局項構(gòu)成,；第二項表示的是局部能量項，由GLIF模型構(gòu)成,。從而使得水平集函數(shù)在局部能量與全局能量的共同控制下向著目標(biāo)區(qū)域的真實(shí)邊界演化,。β∈[0，1]是一個常數(shù),，全局能量項與局部能量項所占比重都由其支配,。對于β的選取要依據(jù)圖像灰度的不均勻程度而定，當(dāng)分割灰度嚴(yán)重不均勻的圖像時,，局部能量起支配作用,，所以此時要選擇較小的β；而當(dāng)分割灰度比較均勻的圖像時,，全局能量起支配作用,，所以此時就要選擇較大的β。式(13)的隱式偏微分方程如下：

3 實(shí)驗結(jié)果

3.1 甲狀腺結(jié)節(jié)分割實(shí)驗結(jié)果

    經(jīng)實(shí)驗測得該模型的時間步長Δt=0.001,，λ₁=1.0,，λ₂=2.4。實(shí)驗平臺是Windows 7旗艦版, PC處理器為intel(R)core(TM)[email protected],，內(nèi)存是4 GB,，軟件版本為MATLAB2012b(64 bit)。

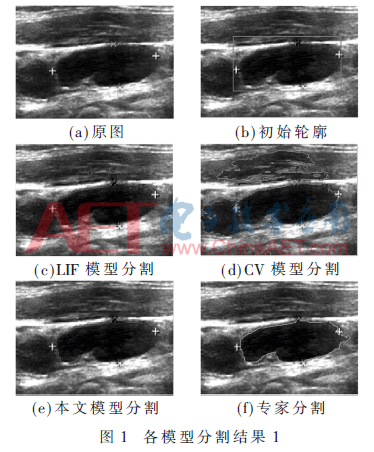
    圖1(a)的整體灰度不均勻,，結(jié)節(jié)局部邊緣模糊,。從實(shí)驗結(jié)果看出，只有本文方法可以準(zhǔn)確地找到結(jié)節(jié)區(qū)域的邊界,。而LIF模型陷入了局部極小值,，CV模型則出現(xiàn)了過分割。

    在圖2中,，結(jié)節(jié)與背景區(qū)域?qū)Ρ榷群艿?，結(jié)節(jié)區(qū)域邊緣模糊,。只有本文模型可以準(zhǔn)確地分割出結(jié)節(jié)區(qū)域，而CV模型與LIF模型都出現(xiàn)了錯誤分割,。

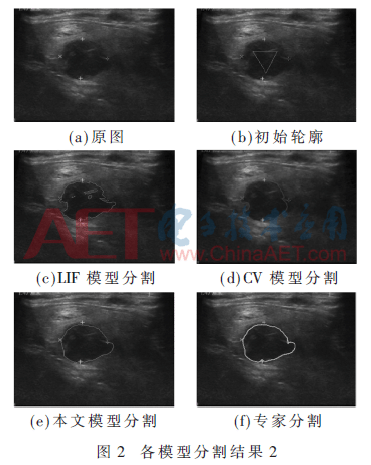
    圖3是一幅被噪聲嚴(yán)重污染的圖片,。從實(shí)驗結(jié)果看,，只有本文方法可以準(zhǔn)確分割出結(jié)節(jié),。LIF模型因為噪聲的干擾而導(dǎo)致錯誤分割。CV模型法的全局?jǐn)M合項,，針對該類圖像很難準(zhǔn)確定位到邊緣,，因此出現(xiàn)過分割現(xiàn)象。

3.2 CV-GLIF模型初始輪廓位置實(shí)驗

    為了驗證本文提出的模型對初始輪廓位置的敏感性程度,，與LIF模型進(jìn)行了對比實(shí)驗,，結(jié)果如圖4所示。

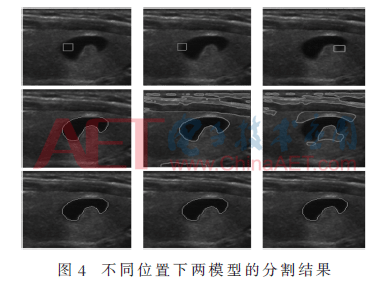
    圖4中,，第一行表示的是所選取的3個初始輪廓的位置,，第二行表示的是LIF模型對應(yīng)于3個位置時的分割結(jié)果，第三行表示是用本文方法進(jìn)行分割時對應(yīng)于3個不同位置的分割結(jié)果,。從實(shí)驗結(jié)果可以看出,，采用LIF模型分割時，只有當(dāng)初始輪廓的位置完全位于結(jié)節(jié)區(qū)域內(nèi)時才能得到較精確的分割結(jié)果,。而本文提出的模型在上述3種位置時都能實(shí)現(xiàn)較精確的分割,。

3.3 實(shí)驗結(jié)果分析

    為了確定實(shí)驗中各個模型的分割精度，本文采用SHATTUCK D W^[7]等提出的骰子相似系數(shù)法(Dice Similarity Coefficient,，DSC)來計算各個模型對應(yīng)的分割精度,，DSC的值越接近于1則表示分割的精度越高。圖1～圖3圖像的DSC值見表1,。

DSC的表達(dá)式為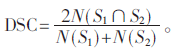其中S₁是由專家手動給出的目標(biāo)區(qū)域的分割圖像,；S₂是由上述模型分割出的目標(biāo)區(qū)域；N(S)表示的是對應(yīng)區(qū)域的面積,，用該區(qū)域中像素的數(shù)目來表示,。

4 結(jié)論

    本文采用了以CV模型為全局能量、以改進(jìn)的LIF模型為局部能量相結(jié)合的水平集方法實(shí)現(xiàn)了甲狀腺結(jié)節(jié)超聲圖像的分割,。 綜合考慮了CV和GLIF兩種模型各自的優(yōu)點(diǎn),，構(gòu)造了能有效分割灰度不均勻圖像的新模型。最后將本文算法的分割結(jié)果與LIF模型和CV模型的分割結(jié)果進(jìn)行對比,。實(shí)驗結(jié)果表明,，本文算法克服了LIF模型與CV模型的缺點(diǎn)，不僅分割精度高,，而且能有效抑制噪聲的干擾,。

參考文獻(xiàn)

[1] HERMUS A R,，HUYSMANS D A.Treatment of Benign nodular thyroid disease[J].The new England Journal of Medicine，1998,，338(20)：1438-1447.

[2] CHAN T F,，VESE L.Active contours without edges[J].IEEE Transactions on Image Processing，2001,，10(2)：266-277.

[3] MUMFORD D,，SHAH J.Optimal approximation by piecewise smooth functions and associated variational problems[J].Communications on Pure & Applied Mathematics，1989,，42(5)：577-685.

[4] Li Chunming,，Kao Chiu-Yen，GORE J C,，et al.Implicit active contours driver by local binary fitting energy[C].IEEE Conference on Computer Vision and Pattern Recognition,，2007：1-7.

[5] ZHANG K H，SONG H,，ZHANG L.Actives contours driven by local image fitting energy[J].Pattern Recognition,，2010，43(4)：1199-1206.

[6] 劉馳,，孫權(quán)森.一種新的結(jié)合圖像梯度的局部活動輪廓模型[J].計算機(jī)應(yīng)用研究,，2014，31(11)：3510-3513.

[7] SHATTUCK D W,，SANDOR-LEAHY S R,，SCHAPER K A，et al.Magnetic resonance image tissue classification using a paaial volume model[J].Neuroimage,，2001,，13(5)：856-876.

作者信息:

王  昕，李  亮

（長春工業(yè)大學(xué) 計算機(jī)科學(xué)與工程學(xué)院,，吉林 長春130012）