0 引言

    粒子群優(yōu)化(Particle Swarm Optimization,，PSO)算法^[1]是由KENNEDY J和EBERHART R C等開發(fā)的一種新的進(jìn)化算法,。相對于遺傳算法^[2]等,，該算法參數(shù)較少、容易實(shí)現(xiàn),，能夠解決復(fù)雜的優(yōu)化問題,，因此在眾多優(yōu)化問題領(lǐng)域都得到了廣泛的應(yīng)用^[3]，如控制決策,、目標(biāo)跟蹤,、深度學(xué)習(xí)等。然而,，粒子群優(yōu)化算法在實(shí)際應(yīng)用中往往難以達(dá)到實(shí)時(shí)性的要求,，特別是求解復(fù)雜的多維問題時(shí)，速度問題更加突出，難以滿足實(shí)際應(yīng)用的需求,。

    隨著嵌入式領(lǐng)域?qū)π阅?、功耗和成本越來越高的要求，多核處理器?yīng)運(yùn)而生^[4],。其中TI公司推出的基于KeyStone架構(gòu)的多核處理器TMS320C6678^[5]是目前業(yè)界最高性能的量產(chǎn)多核DSP,。其具有8個(gè)1.25 GHz DSP內(nèi)核，最高可實(shí)現(xiàn)160 GFLOP的性能,。與FPGA相比其具有更好的浮點(diǎn)性能和實(shí)時(shí)處理能力,，并且具有較高的靈活性和可編程性，為實(shí)現(xiàn)更為復(fù)雜的算法提供了便利,。因此其在4G通信,、航空電子、機(jī)器視覺等領(lǐng)域得到了廣泛的應(yīng)用,。

    本文針對粒子群算法在實(shí)際應(yīng)用中的實(shí)時(shí)性需求，在對算法進(jìn)行并行性分析的基礎(chǔ)上,，根據(jù)TMS320C6678多核處理器的架構(gòu)特點(diǎn),，設(shè)計(jì)出高效的應(yīng)用程序，充分發(fā)揮了TMS320C6678的性能優(yōu)勢,，有效地提高了系統(tǒng)的實(shí)時(shí)處理能力,。實(shí)驗(yàn)數(shù)據(jù)表明了該設(shè)計(jì)的合理性與有效性。

1 PSO算法簡介

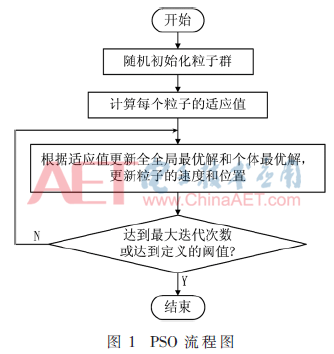
    PSO流程圖如圖1所示,。粒子群算法的數(shù)學(xué)描述如下：m維的解空間中,，X={x₁，x₂,，…,，x_n}表示整個(gè)種群，該種群由n個(gè)粒子組成,。因此整個(gè)種群中的第i個(gè)粒子的位置可以表示為x_i={x_i1,，x_i2，…,，x_im},，該粒子對應(yīng)的求解速度可以表示為v_i={v_i1，v_i2,，…,，v_im}，每個(gè)粒子對應(yīng)的個(gè)體最優(yōu)解表示為p_i={p_i1,，p_i2,，…，p_im}，整個(gè)種群的全局最優(yōu)解可以表示為g_i={g_i1,，g_i2,，…，g_im},。在每一次的迭代中,，每個(gè)粒子將個(gè)體最優(yōu)解pbest和全局最優(yōu)解gbest作為飛行經(jīng)驗(yàn)，根據(jù)如下公式來更新自己的速度和位置：

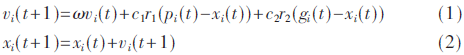
式中,，t表示當(dāng)前迭代次數(shù),，x_i(t)對應(yīng)粒子當(dāng)前時(shí)刻的位置，x_i(t+1)對應(yīng)粒子下一時(shí)刻的位置,，v_i(t)和v_i(t+1)分別表示粒子當(dāng)前時(shí)刻和下一時(shí)刻的速度,，ω為慣性因子，c₁和c₂為學(xué)習(xí)因子,，r₁和r₂表示在0~1之間的隨機(jī)數(shù),。此外在每一維，粒子都有最大的限制速度v_max,，如果v_i>v_max,，則有v_i=v_max；如果v_i<v_max,，則有v_i=-v_max,。

2 多核DSP任務(wù)并行設(shè)計(jì)

2.1 算法并行性分析

    粒子群算法和其他一些進(jìn)化算法相比，其優(yōu)勢在于步驟簡單,、參數(shù)少,、容易實(shí)現(xiàn)、無需梯度信息等,。更重要的是粒子群算法是一種并行算法,，非常適合在多核處理器上實(shí)現(xiàn)其并行計(jì)算。算法中各個(gè)粒子具有很高的獨(dú)立性,，所以各個(gè)粒子可以獨(dú)立地完成信息的更新,，從根本上實(shí)現(xiàn)各個(gè)粒子間的并行操作處理，提高算法的實(shí)時(shí)性,。根據(jù)處理器的核心數(shù),，將粒子的更新任務(wù)平均映射到8個(gè)核上。運(yùn)行時(shí)使用如下基本測試函數(shù)對該方案進(jìn)行驗(yàn)證：

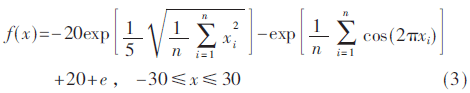
其中,，n表示維數(shù),，該函數(shù)在x=(0，0,，…,，0)處取得全局最小值f_max=0,。另外該函數(shù)比較復(fù)雜，是一個(gè)多峰函數(shù),。

2.2 并行處理模型設(shè)計(jì)

    將程序映射到多核處理器的第一步就是確定任務(wù)的并行性,，并選擇一種最合適的處理模型。前面已經(jīng)分析了算法的并行性,。

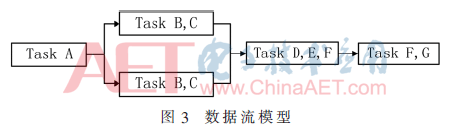
    兩種最主要的模型是主從模型和數(shù)據(jù)流模型^[6],，分別如圖2、圖3所示,。主從模型是一種控制集中,、執(zhí)行分布的模型。數(shù)據(jù)流模型代表分布式控制和執(zhí)行,。除此之外還有OpenMP模型^[7],，該模型是一種在共享內(nèi)存并行體系中應(yīng)用發(fā)展多線程的應(yīng)用程序編程接口，如圖4所示,。

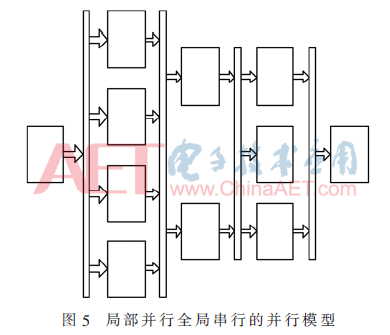
    結(jié)合前面算法的并行性分析,，考慮到處理流程時(shí)間上的并行性和空間上的并行性，這其中包含了流水操作和并發(fā)操作,，使用單一的模型都無法有效地解決,，因此，突破性地將二者結(jié)合起來,，設(shè)計(jì)出局部并行全局串行的并行模型，如圖5所示,，從而取得良好的并行度和加速比,，這在測試數(shù)據(jù)及結(jié)果分析中可以看出。

2.3 處理器之間的通信交流

    多核處理器中內(nèi)核之間如何進(jìn)行高效的通信交流,，是多核系統(tǒng)所面臨的主要難點(diǎn),。處理器之間的通信交流主要包括數(shù)據(jù)移動(dòng)和同步^[8]。TMS320C6678提供了多種處理器之間的通信機(jī)制,。軟件是基于SYS/BIOS實(shí)時(shí)操作系統(tǒng)開發(fā)的,。考慮到開發(fā)的難易程度及性能,，采用IPC核間通信的組件來完成核間數(shù)據(jù)搬移和同步,。該組件有“消息隊(duì)列”(MessageQ)和“通知”(Notify)兩種模型。除了Notify通知機(jī)制,，還可以利用MessageQ來實(shí)現(xiàn)更為復(fù)雜的核間通信,。考慮到需要同時(shí)實(shí)現(xiàn)數(shù)據(jù)搬移和同步,，所以采用“消息隊(duì)列”(MessageQ)模型,。0核作為主核負(fù)責(zé)向從核發(fā)送事件,，激活從核并進(jìn)行一定的運(yùn)算。主核與從核之間有相互連接,。1~7核為從核,，主要負(fù)責(zé)運(yùn)算，從核之間沒有連接,。

3 基于TMS320C6678的PSO算法的實(shí)現(xiàn)

    軟件部分是基于SYS/BIOS操作系統(tǒng)開發(fā)的,，同時(shí)利用IPC組件。在實(shí)現(xiàn)過程中,，利用DSP集成開發(fā)環(huán)境CCS5.2進(jìn)行相應(yīng)的編程開發(fā),。SYS/BIOS用來實(shí)現(xiàn)核間任務(wù)調(diào)度，IPC用來實(shí)現(xiàn)核間同步和通信,。

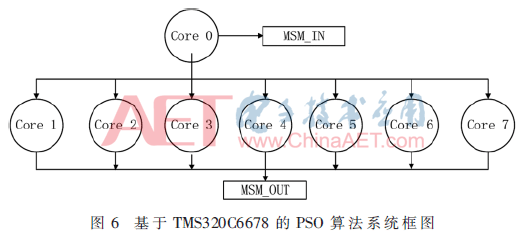
    基于TMS320C6678的PSO算法系統(tǒng)框圖如圖6所示,。首先是系統(tǒng)啟動(dòng)，8個(gè)核進(jìn)行相應(yīng)的初始化配置,。初始化配置之后調(diào)用Ipc_start()函數(shù)將自動(dòng)實(shí)現(xiàn)相應(yīng)模塊的配置,，各個(gè)核進(jìn)入同步等待的狀態(tài)，直到8個(gè)核都進(jìn)入同步等待狀態(tài),，程序才會(huì)繼續(xù)執(zhí)行,。一般情況下，在使用IPC組件時(shí)直接讓每個(gè)核同所有核之間都有連接,，而且各核之間連接都是相同且雙向的,，這樣的配置方法并不高效，影響運(yùn)行效率,。因此這里有選擇地進(jìn)行核間連接,，使用Ipc.ProcSync_PAIR在.cfg文件中進(jìn)行配置，之后使用Ipc_attach()函數(shù)僅僅在主核與從核之間建立雙向連接,。主核首先進(jìn)行整個(gè)粒子群的初始化,，主要包括隨機(jī)產(chǎn)生粒子的位置和速度，計(jì)算出每個(gè)粒子的適應(yīng)度值作為局部最優(yōu)解,，求出對應(yīng)的全局最優(yōu)解等任務(wù),。主核在完成初始化工作后，將數(shù)據(jù)分為8份,，通過MesssageQ_put()函數(shù)將每個(gè)核對應(yīng)的數(shù)據(jù)的地址發(fā)送到對應(yīng)的核,，并啟動(dòng)從核進(jìn)行相應(yīng)的處理。之后所有的核進(jìn)行循環(huán)迭代處理,，實(shí)現(xiàn)算法對應(yīng)的進(jìn)化尋優(yōu)處理,。同時(shí)判斷當(dāng)前解是否滿足預(yù)定的最小適應(yīng)閾值或達(dá)到最大迭代次數(shù)。最后直到從核完成迭代,，通知主核完成所有運(yùn)算,，輸出最優(yōu)解,。

4 實(shí)驗(yàn)結(jié)果分析

4.1 存儲(chǔ)空間分析

    KeyStone架構(gòu)是一款精心設(shè)計(jì)且效率極高的多核心內(nèi)存架構(gòu)，其具備3個(gè)存儲(chǔ)等級^[9],。處理器的每個(gè)內(nèi)核都擁有自己的一級程序（L1P）和數(shù)據(jù)(L1D)存儲(chǔ)器,，均為32 KB大小，這里默認(rèn)配置成cache使用,。二級存儲(chǔ)器L2可以做代碼和數(shù)據(jù)存儲(chǔ)器,，為了提高程序性能，這里把L2的32 KB大小的空間也設(shè)置成cache,，其余空間用作SRAM,。當(dāng)數(shù)據(jù)量太大時(shí)需要將數(shù)據(jù)置于DDR3中。該實(shí)驗(yàn)中設(shè)計(jì)粒子的個(gè)數(shù)為50,，維度也為50,，則算法對應(yīng)的數(shù)據(jù)量大概為60 KB。另外考慮到共享存儲(chǔ)器有4 MB大小,，可以將程序運(yùn)行涉及的主要數(shù)據(jù)存放在共享存儲(chǔ)器里,，包括粒子的位置、速度,、個(gè)體最優(yōu)解,、全局最優(yōu)解等。占用全部片內(nèi)共享存儲(chǔ)器（MSM）資源的1.5%左右,。CCS仿真時(shí)的平均收斂曲線如圖7所示,。

4.2 運(yùn)行時(shí)間分析

    TMS320C6678處理器每個(gè)內(nèi)核頻率為1.25 GHz，可以提供每秒高達(dá)40 GB MAC定點(diǎn)運(yùn)算和20 GFLOP浮點(diǎn)運(yùn)算能力,；1片8核的TMS320C6678提供等效達(dá)10 GHz的內(nèi)核頻率,，單精度浮點(diǎn)并行運(yùn)算能力理論上可達(dá)160 GB FLOP。實(shí)驗(yàn)中有關(guān)算法的運(yùn)行時(shí)間是通過C語言庫中的clock()函數(shù)測量的,。處理器運(yùn)行時(shí)的主頻配置為1.0 GHz,，則算法迭代500次時(shí)運(yùn)行時(shí)鐘數(shù)如表1所示,。

    由表1可以看出,，基于TMS320C6678的PSO算法系統(tǒng)得到了較好的核間通信和并行處理性能。在相同的參數(shù)環(huán)境下,，該系統(tǒng)的處理能力是C66x單核的5.19倍,。實(shí)驗(yàn)結(jié)果表明，基于TMS320C6678的并行粒子群算法的實(shí)時(shí)處理能力有顯著提升,。

4.3 加速比和并行效率

    加速比^[10]和并行效率是衡量并行處理器性能的兩個(gè)重要的指標(biāo),。加速比(Speedup Rate)用來衡量并行系統(tǒng)或程序并行化的性能和效果。并行效率(Parallel Efficiency)表示在并行機(jī)執(zhí)行并行算法時(shí),，平均每個(gè)處理機(jī)的執(zhí)行效率,。下面根據(jù)Amdahl定律^[11]來具體計(jì)算加速比和并行效率,。

    假設(shè)一個(gè)任務(wù)在有N個(gè)單元的處理器上運(yùn)行，其中可并行執(zhí)行的部分為T_p,，只能串行的部分為T_s,。則在單處理器上運(yùn)行時(shí)間為T_ser=T_s+T_p，T_par=T_s+T_p/P,。這里用Sr來表示加速比,，則根據(jù)表1測試的數(shù)據(jù)可以求出該系統(tǒng)的加速比如下：

    通過以上分析可以看出，通過增加并行處理單元個(gè)數(shù)可以提高加速比,，但是其增加的倍數(shù)和增加的處理器的個(gè)數(shù)并不是嚴(yán)格對應(yīng)的,。這是因?yàn)樘幚砥鱾€(gè)數(shù)的增加會(huì)帶來額外的通信開銷，甚至在某些情況下會(huì)導(dǎo)致系統(tǒng)效率的下降,。因此在設(shè)計(jì)系統(tǒng)時(shí),，應(yīng)綜合考慮處理單元個(gè)數(shù)、并行結(jié)構(gòu)設(shè)計(jì)和任務(wù)的映射等因素,。

5 結(jié)論

    本文針對粒子群算法在實(shí)際應(yīng)用中的實(shí)時(shí)性需求,，首先對算法進(jìn)行并行性分析，并根據(jù)TMS320C6678多核處理器的架構(gòu)特點(diǎn),，設(shè)計(jì)出局部并行全局串行的并行模型,，高效地將應(yīng)用程序映射到多核處理器。該設(shè)計(jì)也適用于其他架構(gòu)的并行處理器,，具有廣泛的應(yīng)用性,。實(shí)驗(yàn)數(shù)據(jù)表明該設(shè)計(jì)充分發(fā)揮了TMS320C6678的性能優(yōu)勢，與單核處理相比有效提高了系統(tǒng)的實(shí)時(shí)處理能力,。因此,，該設(shè)計(jì)有效地推進(jìn)了PSO算法在實(shí)際中的應(yīng)用，對其他各種群智能算法有重要的借鑒意義,。

參考文獻(xiàn)

[1] KENNEDY J,，EBERHART R C.Particle swarm optimization[C].IEEE International Conference on Neural Networks，1995：1942-1948.

[2] DEB K,，PRATAP A,，AGARWAL S，et al.A fast and elitist multiobjective genetic algorithm：NSGA-II[J].IEEE Transactions on Evolutionary Computation,，2002,，6(2)：182-197.

[3] Jin Nanbo,RAHMAT-SAMII Y.Advances in particle swarm optimization for antenna designs：real-number，Binary,，single-objective and multiobjective implementations[J].IEEE Transactions on Antennas and Propagation,，2007，55(3)：556-567.

[4] 郝朋朋,，周煦林,，唐藝菁,，等.基于TMS320C6678多核處理器體系結(jié)構(gòu)的研究[J].微電子學(xué)與計(jì)算機(jī)，2012,，29(12)：171-175.

[5] Texas Instruments.TMS320C6678 mulicore fixed and floating-point digital signal processor[Z].2010.

[6] Texas Instruments. Multicore programming guide(Literature Number：SPRAB27B)[Z].2011.

[7] 牛金海.TMS320C66x KeyStone架構(gòu)多核DSP入門與實(shí)例精解[M].上海：上海交通大學(xué)出版社,，2014.

[8] 吳灝，肖吉陽,，范紅旗,，等.TMS320C6678多核DSP的核間通信方法[J].電子技術(shù)應(yīng)用，2012,，38(9)：11-13.

[9] Texas Instruments.KeyStone architecture multicore shared memory controller(MSMC)(Literature Number：SPRUGW7A)[Z].2011.

[10] 謝超,，麥聯(lián)叨，都志輝,，等.關(guān)于并行計(jì)算系統(tǒng)中加速比的研究與分析[J].計(jì)算機(jī)工程與應(yīng)用,，2003，39(26)：66-68.

[11] 李文石,，姚宗寶.基于阿姆達(dá)爾定律和蘭特法則計(jì)算多核架構(gòu)的加速比[J].電子學(xué)報(bào),，2012，40(2)：230-234.