文獻(xiàn)標(biāo)識(shí)碼: A
DOI:10.16157/j.issn.0258-7998.182787
中文引用格式: 應(yīng)俊,朱云鵬,賀超. 基于改進(jìn)的SVD和Prony的諧波檢測算法[J].電子技術(shù)應(yīng)用,2019,45(1):46-50.
英文引用格式: Ying Jun,Zhu Yunpeng,He Chao. Harmonic detection algorithm based on improved SVD and Prony[J]. Application of Electronic Technique,2019,45(1):46-50.
0 引言
隨著科學(xué)技術(shù)的不斷發(fā)展,大量的非線性負(fù)載和電力電子設(shè)備被應(yīng)用在工業(yè)生產(chǎn)和日常生活中,這提高了生產(chǎn)效率,促進(jìn)了生活便利,但同時(shí)也對(duì)電網(wǎng)造成了巨大的諧波污染。另一方面,隨著新能源在電力系統(tǒng)中的迅速發(fā)展,各種分布式的電源也相繼產(chǎn)生,比如太陽能發(fā)電、風(fēng)力發(fā)電以及地?zé)崮艿龋@些新能源的發(fā)電設(shè)備并網(wǎng)運(yùn)行時(shí),同樣也給電力系統(tǒng)帶來了一系列諧波污染,因此諧波污染治理也越發(fā)重要[1]。諧波污染治理的性能很大程度上又受到諧波檢測環(huán)節(jié)的影響,這就要求諧波檢測過程必須要具備兩個(gè)特點(diǎn):實(shí)時(shí)性強(qiáng)、準(zhǔn)確度高[2]。電力系統(tǒng)中常用的諧波檢測的方法主要有傅里葉變換[3]、小波變換[4]和希爾伯特-黃變換[5]等。在治理諧波污染時(shí)性能表現(xiàn)不佳,分別體現(xiàn)在易產(chǎn)生頻譜泄漏和柵欄效應(yīng)、算法計(jì)算量過大和不具有自適應(yīng)性以及容易產(chǎn)生模態(tài)混疊效應(yīng)和負(fù)頻率。
近年來,Prony算法因其具有高頻率分辨率和高頻率估計(jì)精度,在電力系統(tǒng)中獲得了越來越多的關(guān)注。但是,Prony算法對(duì)于噪聲較為敏感,易受噪聲信號(hào)的影響。電網(wǎng)系統(tǒng)中包含著大量的高斯噪聲,因此如何能夠降低噪聲對(duì)模型辨識(shí)的影響成為了一個(gè)難點(diǎn)。文獻(xiàn)[6]提出了Prony算法與小波分析相結(jié)合的方法,先通過小波函數(shù)對(duì)擾動(dòng)信號(hào)進(jìn)行分解,然后利用改進(jìn)的Prony算法對(duì)穩(wěn)態(tài)擾動(dòng)問題進(jìn)行參數(shù)辨識(shí),雖然提高了辨識(shí)精度,但是該算法過于依賴對(duì)小波基的選擇,濾波效果并不理想。文獻(xiàn)[7]提出了將SVD濾波技術(shù)與Prony算法相結(jié)合的方法,該方法利用SVD的特性濾除噪聲信號(hào),其次利用Prony算法對(duì)信號(hào)進(jìn)行處理,但是SVD濾波處理過程中太過依賴奇異值有效階次的判斷,同樣不具備自適應(yīng)性。
本文在前人研究的基礎(chǔ)上,提出了一種基于SVD的改進(jìn)濾波算法,能夠精確地找到電網(wǎng)信號(hào)中諧波及間諧波信號(hào)分量的階次,同時(shí)濾除電網(wǎng)信號(hào)中的噪聲信號(hào),只留下“純凈的”電網(wǎng)信號(hào)。根據(jù)濾波后的電網(wǎng)信號(hào)以及諧波及間諧波信號(hào)階數(shù),利用一種改進(jìn)的Prony算法,結(jié)合線性神經(jīng)網(wǎng)絡(luò),計(jì)算出信號(hào)的頻率、相位和幅值。研究結(jié)果表明,算法對(duì)于諧波信號(hào)的檢測精確度極高,同時(shí)由于所需的采樣數(shù)據(jù)長度小,實(shí)時(shí)性也較強(qiáng),能夠很好地滿足實(shí)時(shí)性和準(zhǔn)確度的要求。
1 電網(wǎng)信號(hào)模型
電網(wǎng)信號(hào)主要包含基波各次諧波、間諧波以及各種噪聲信號(hào),因此可以通過以下數(shù)學(xué)表達(dá)式來建立模型:

式中,wi=2πfi,p為諧波和間諧波個(gè)數(shù),Ai、fi、θi分別表示第i個(gè)諧波或間諧波信號(hào)的幅值、頻率和相位,而ω(n)則表示電網(wǎng)系統(tǒng)中的噪聲信號(hào)。
根據(jù)電網(wǎng)的特性,除了基波分量以外,奇次諧波分量對(duì)電網(wǎng)的影響所占權(quán)重較大,本文主要選取了奇次諧波中影響較大的3次、5次以及7次諧波作為電網(wǎng)信號(hào)的模型[8];間諧波主要存在于諧波附近,易受諧波信號(hào)影響。因此,本文基于諧波信號(hào)選擇了3個(gè)間諧波信號(hào)。諧波檢測算法的作用是對(duì)式(1)的正弦信號(hào)進(jìn)行參數(shù)辨識(shí),得到各個(gè)諧波和間諧波信號(hào)的特性參數(shù),本文所提算法正是基于此電網(wǎng)信號(hào)模型。
2 算法實(shí)現(xiàn)
2.1 基于SVD的改進(jìn)濾波算法
電網(wǎng)信號(hào)模型為x(i)=s(i)+w(i)(i=1,2,…,N)。將接收到的電能信號(hào)序列x=[x1,x2,…,xN]構(gòu)造成如下的Hankel矩陣的形式:

其中,當(dāng)N為偶數(shù)時(shí),n=N/2,m=N/2+1;當(dāng)N為奇數(shù)時(shí)n=(N+1)/2,m=(n+1)/2。
完成對(duì)信號(hào)序列的Hankel矩陣X的構(gòu)造以后,對(duì)X進(jìn)行奇異值分解,可得到:

信號(hào)的完備空間可以劃分為信號(hào)子空間和噪聲子空間,并且它們之間相互正交。在奇異值分解理論中,奇異值的前k個(gè)值對(duì)應(yīng)著信號(hào)子空間分量,后q-k個(gè)奇異值則對(duì)應(yīng)著噪聲子空間分量。因此,稱k為信號(hào)的有效階次。
信號(hào)分解的奇異值序列的分布具有其特點(diǎn):在有效階次k之前,奇異值內(nèi)部差異都相對(duì)較小,變化也比較平緩;而在第k+1個(gè)奇異值處,奇異值序列出現(xiàn)明顯的階躍式下降;之后奇異值序列的變化再次趨于平緩,不存在明顯波動(dòng)[9]。如果將獲得的奇異值序列看作一個(gè)信號(hào)序列,根據(jù)奇異值序列的這種特性尋找到相應(yīng)的突變點(diǎn)作為奇異點(diǎn),那么這個(gè)突變點(diǎn)的位置就是原信號(hào)中有效階次。
對(duì)于電網(wǎng)信號(hào)來說,在確定有效階次為k后,如果k的值過小,雖然大部分噪聲信號(hào)都被濾除,但是大量的電能信號(hào)也已丟失;如果k的值過大,電能信號(hào)雖保持完整,但是噪聲信號(hào)未能得到很好的濾除,干擾仍較大。因此,如何更好地確定有效階次對(duì)于濾波的效果至關(guān)重要。本文在結(jié)合對(duì)電網(wǎng)信號(hào)的特性分析以及奇異值分解理論后,提出一種奇異點(diǎn)輔助算法,根據(jù)奇異值增長率的變化,確定奇異值突變點(diǎn),輔助確定奇異值的有效階次。奇異值增長率公式為:

式中,σi為第i個(gè)奇異值,ηi為第i+1個(gè)奇異值同比上一個(gè)奇異值的下降率。通過對(duì)ηi大小的比較,選擇ηi最大的i處作為奇異點(diǎn)位置。
對(duì)矩陣X進(jìn)行奇異值分解之后,利用式(6)對(duì)信號(hào)進(jìn)行重構(gòu):

2.2 改進(jìn)的Prony-ADALINE算法
Prony算法是一種使用指數(shù)函數(shù)的線性組合來描述等間距采樣數(shù)據(jù)的理論,可以用來估計(jì)有理式功率譜密度[10]。傳統(tǒng)的算法采用的數(shù)學(xué)模型為p個(gè)具有任意幅值、相位、頻率與衰減因子的指數(shù)函數(shù),本文的信號(hào)為正弦信號(hào),因此,采樣Prony譜線估計(jì)算法[11],其數(shù)學(xué)模型為p個(gè)實(shí)的、無衰減的正弦信號(hào)。
2.2.1 Prony譜線估計(jì)算法
Prony譜線估計(jì)算法的數(shù)學(xué)模型用離散時(shí)間的函數(shù)表示為:


本文改進(jìn)的算法主要包括以下步驟:
(1)定義樣本函數(shù)(10),根據(jù)濾波處理后的信號(hào)以及得到的信號(hào)的有效階次k(即特征多項(xiàng)式中2p=k),利用樣本函數(shù)構(gòu)建樣本矩陣,并通過樣本矩陣構(gòu)建法方程(11):

2.2.2 ADALINE神經(jīng)網(wǎng)絡(luò)算法
ADALINE神經(jīng)網(wǎng)絡(luò)是一種結(jié)構(gòu)較為簡單的神經(jīng)網(wǎng)絡(luò)模型,現(xiàn)在已經(jīng)廣泛應(yīng)用于自適應(yīng)信號(hào)處理領(lǐng)域,對(duì)于電網(wǎng)信號(hào)中的諧波和間諧波信號(hào)分析也同樣適用。ADALINE神經(jīng)網(wǎng)絡(luò)算法和其他神經(jīng)網(wǎng)絡(luò)相比,它的最大優(yōu)勢就是不需要事先對(duì)神經(jīng)網(wǎng)絡(luò)進(jìn)行大量訓(xùn)練,同時(shí)它還具有分析精度高、收斂速度快這一突出特點(diǎn),因此可以做到對(duì)電網(wǎng)信號(hào)中的諧波和間諧波信號(hào)成分的實(shí)時(shí)分析。
根據(jù)三角函數(shù)的特點(diǎn),對(duì)式(8)進(jìn)行三角恒等變換,得到式(13):

基于ADALINE模型的檢測原理圖如圖1所示,分為輸入層、求和層和輸出層。其中輸入信號(hào)X(n)= [ cos(2πf1n),sin(2πf1n),…,cos(2πfpn),sin(2πfpn)],輸入神經(jīng)元數(shù)即等于有效階次2p。對(duì)應(yīng)的權(quán)系數(shù)為W(n)=[a1,b1,…,ap,bp]T。輸入信號(hào)與權(quán)系數(shù)相乘,經(jīng)過求和層,得到單個(gè)的輸出向量y(n)。權(quán)值更新算法自動(dòng)更新權(quán)系數(shù)W(n),使之不斷收斂到穩(wěn)態(tài)階段,這時(shí)的權(quán)系數(shù)即為逼近式(13)中的系數(shù),實(shí)現(xiàn)諧波及間諧波的幅值、相位檢測。
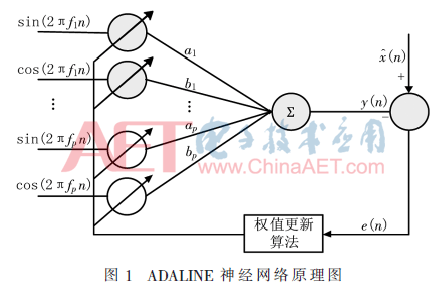
該神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)的基本特點(diǎn)可總結(jié)為如下三個(gè)方面:
(1)可以根據(jù)變化著的輸入和目標(biāo)輸出實(shí)現(xiàn)實(shí)時(shí)在線訓(xùn)練;
(2)應(yīng)用自適應(yīng)在線算法調(diào)整各權(quán)值大小;
(3)結(jié)構(gòu)簡單,便于硬件實(shí)現(xiàn)。
3 仿真分析
實(shí)際電網(wǎng)中,電網(wǎng)信號(hào)相對(duì)比較復(fù)雜,包含了眾多的諧波、間諧波以及噪聲信號(hào)等。本節(jié)主要對(duì)電網(wǎng)電壓信號(hào)進(jìn)行仿真并分析,建立的信號(hào)模型的表達(dá)式如式(14)所示,通過利用MATLAB軟件對(duì)信號(hào)進(jìn)行仿真分析,用以分析和驗(yàn)證本文所提算法應(yīng)用在諧波檢測的性能。

式中,ω(t)為加在諧波信號(hào)上的噪聲,信噪比為30 dB,各個(gè)諧波以及間諧波的具體參數(shù)如表1所示。本次信號(hào)采樣點(diǎn)個(gè)數(shù)為400,采樣頻率為1 500 Hz,采樣時(shí)間為0.27 s。

3.1 濾波算法性能分析
對(duì)于采樣的電網(wǎng)信號(hào),根據(jù)式(2)構(gòu)造Hankel矩陣X,對(duì)其進(jìn)行奇異值分解,得到奇異值序列σ。根據(jù)本文提出的奇異值輔助算法,通過對(duì)奇異值序列的運(yùn)算,得到如圖2所示的奇異值增長率曲線。

圖2中橫坐標(biāo)表示的為奇異值序列,縱坐標(biāo)為根據(jù)輔助算法計(jì)算出的奇異值增長率。由圖2可知,奇異值增長率在橫坐標(biāo)為0~14區(qū)間變化較大;在超過14后,增長率降低,接近于0,變化趨于穩(wěn)定。這是因?yàn)楦鞔沃C波分量的能量差距較大導(dǎo)致。增長率在奇異值序列為2時(shí)達(dá)到80%以上,是由于基頻信號(hào)與其他諧波成分能量相差過大。當(dāng)奇異值序列取值為14時(shí),此時(shí)的增長率接近于1,達(dá)到最大值。對(duì)比數(shù)據(jù)可知,該處即為有效階次,通過該輔助算法確定的有效階次與實(shí)際的完全一致。
根據(jù)已經(jīng)得到的奇異值的有效階次,對(duì)信號(hào)進(jìn)行SVD濾波處理,濾波結(jié)果如圖3所示。圖3中分別是未加噪聲的原始諧波信號(hào)、加噪聲的諧波信號(hào)以及SVD濾波后的諧波信號(hào)的局部波形圖。
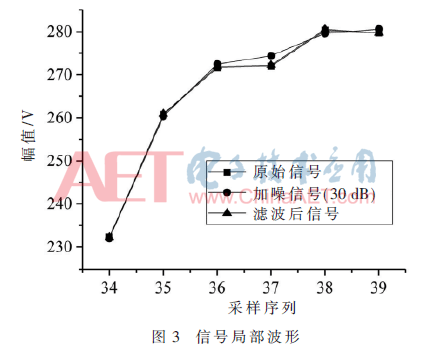
從圖3中原始信號(hào)、包含噪聲信號(hào)以及濾波后信號(hào)的對(duì)比可看出,濾波后的信號(hào)波形幾乎與原始信號(hào)完全重合。這是因?yàn)楸疚奶岢龅乃惴軌驕?zhǔn)確地確定信號(hào)的有效階次,進(jìn)而能夠有效濾除噪聲成分,降低噪聲對(duì)諧波檢測算法影響的同時(shí),又沒有損失信號(hào)中的有效成分,為Prony譜線估計(jì)算法提供了一個(gè)“純凈”的電能信號(hào)。
3.2 諧波檢測算法性能分析
為了驗(yàn)證本文方法的有效性,通過采樣本文所提算法與文獻(xiàn)[12]中的數(shù)學(xué)形態(tài)學(xué)+改進(jìn)Prony算法進(jìn)行對(duì)比,其中,算法1為本文算法,算法2為文獻(xiàn)中所提算法。兩種算法對(duì)于信號(hào)特性參數(shù)中頻率的估計(jì)結(jié)果如表2所示,對(duì)于幅值和相位特性參數(shù)的估計(jì)則通過圖4以相對(duì)誤差的形式給出。
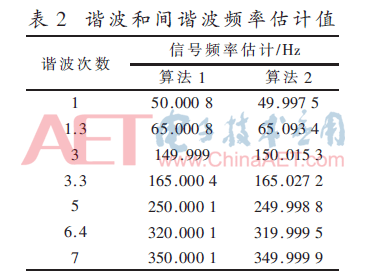

表2是兩種算法對(duì)于電網(wǎng)信號(hào)對(duì)頻率估計(jì)的計(jì)算數(shù)值結(jié)果,兩種算法對(duì)于諧波分量的頻率估計(jì)誤差已經(jīng)很小,接近實(shí)際頻率值,估計(jì)精確度極高。其中在對(duì)于間諧波分量的頻率進(jìn)行計(jì)算時(shí)發(fā)現(xiàn),算法2在對(duì)于1.3次間諧波的頻率進(jìn)行計(jì)算時(shí),計(jì)算值與實(shí)際參數(shù)值相差0.093 4 Hz,而算法1的計(jì)算值與實(shí)際參數(shù)值誤差則僅為0.000 8 Hz,在3.3次間諧波分量處算法2的計(jì)算誤差同樣遠(yuǎn)大于算法1,而在6.4次間諧波處兩種算法的計(jì)算誤差逐漸降低,趨于平緩。
圖4表示的是兩種算法對(duì)于幅值和相位這兩個(gè)參數(shù)計(jì)算數(shù)值的相對(duì)誤差。由圖可知,算法1對(duì)于幅值的計(jì)算在1.3以及3.3次諧波處的相對(duì)誤差遠(yuǎn)小于算法2的相對(duì)誤差,且計(jì)算結(jié)果滿足文獻(xiàn)[13]中規(guī)定的A類測量儀器要求的相對(duì)誤差小于5%。在對(duì)于相位計(jì)算過程中,算法1計(jì)算的相對(duì)誤差最高也僅為1.5%,檢測精確度比算法2更高。
4 結(jié)論
本文針對(duì)Prony算法對(duì)噪聲信號(hào)敏感的問題,提出了一種基于SVD改進(jìn)算法。采用了自適應(yīng)的輔助算法幫助奇異值序列找到有效階次,替代了傳統(tǒng)的奇異值曲線以及奇異熵增量等經(jīng)驗(yàn)性的方法,更好地濾除噪聲信號(hào)。同時(shí),基于有效階次,將SVD更好地與Prony算法結(jié)合在一起,使用簡單的線性方程組的求解去替代最小二乘法,降低了算法運(yùn)算量。在此基礎(chǔ)上進(jìn)行仿真驗(yàn)證,仿真結(jié)果表明該方法準(zhǔn)確、有效,具有一定的工程應(yīng)用價(jià)值。
參考文獻(xiàn)
[1] BAGHERI A,MARDANEH M,RAJAEI A,et al.Detection of grid voltage fundamental and harmonic components using Kalman filter and generalized averaging method[J].IEEE Transactions on Power Electronics,2015,31(2):1064-1073.
[2] 彭詠龍,張坤鋒,李亞斌,等.基于自適應(yīng)算法的諧波檢測方法研究[J].電測與儀表,2018,55(9):6-9.
[3] Su Taixin,Yang Mingfa,Jin Tao,et al.Power harmonic and interharmonic detection method in renewable power based on Nuttall double-window all-phase FFT algorithm[J].IET Renewable Power Generation,2018,12(8):953-961.
[4] TSE N C F,CHAN J Y C,LAU W H,et al.Hybrid wavelet and hilbert transform with frequency-shifting decomposition for power quality analysis[J].IEEE Transactions on Instrumentation and Measurement,2012,61(12):3225-3233.
[5] 李正明,徐敏,潘天紅,等.基于小波變換和HHT的分布式并網(wǎng)系統(tǒng)諧波檢測方法[J].電力系統(tǒng)保護(hù)與控制,2014,42(4):34-39.
[6] 任子暉,劉昊岳,徐進(jìn)霞.基于小波變換和改進(jìn)Prony方法的電能質(zhì)量擾動(dòng)分析[J].電力系統(tǒng)保護(hù)與控制,2016,44(9):122-128.
[7] 許伯強(qiáng),田士華.SVD濾波技術(shù)與Prony譜線估計(jì)算法相結(jié)合的異步電動(dòng)機(jī)轉(zhuǎn)子故障檢測新方法[J].電機(jī)與控制應(yīng)用,2015,42(10):41-47.
[8] 劉冬梅,楊重良,張艷,等.基于Nuttall自卷積窗四譜線插值FFT的電力諧波分析方法[J].合肥工業(yè)大學(xué)學(xué)報(bào),2018,41(3):12-17.
[9] 查翔,倪世宏,謝川,等.奇異值分解去噪中有效秩階次的自身輔助確定[J].計(jì)算機(jī)應(yīng)用研究,2016,33(5):1359-1362.
[10] 熊杰鋒.基于加窗插值和Prony的電力系統(tǒng)間諧波算法[J].電力系統(tǒng)保護(hù)與控制,2011,39(7):8-13,19.
[11] 張賢達(dá).現(xiàn)代信號(hào)處理[M].北京:清華大學(xué)出版社,2002.
[12] 公茂法,蔡芬,劉俊杰,等.基于數(shù)學(xué)形態(tài)學(xué)和改進(jìn)Prony算法的諧波與間諧波參數(shù)估計(jì)[J].電測與儀表,2018,55(11):25-29,40.
[13] GB/T 24337-2009,電能質(zhì)量 公用電網(wǎng)間諧波[S].2009.
作者信息:
應(yīng) 俊1,2,朱云鵬1,2,賀 超2
(1.重慶郵電大學(xué) 光電工程學(xué)院,重慶400065;2.重慶郵電大學(xué) 光通信與網(wǎng)絡(luò)重點(diǎn)實(shí)驗(yàn)室,重慶400065)

