0 引言

    短期電力負(fù)荷預(yù)測(cè)是電力系統(tǒng)運(yùn)行和調(diào)度的關(guān)鍵問(wèn)題,，它是電力系統(tǒng)經(jīng)濟(jì)運(yùn)行的前提，有效的電力負(fù)荷預(yù)測(cè)不僅對(duì)電網(wǎng)規(guī)劃,，而且對(duì)其安全穩(wěn)定經(jīng)濟(jì)運(yùn)行有著重要的影響^[1],。

    電力負(fù)荷預(yù)測(cè)作為一項(xiàng)基礎(chǔ)性研究，長(zhǎng)期以來(lái)一直受到人們的重視,。許多專家學(xué)者對(duì)預(yù)測(cè)理論和方法做了大量的研究,，并提出了若干預(yù)測(cè)模型和方法。目前,，負(fù)荷預(yù)測(cè)的方法有很多，主要可分為兩類：一類是統(tǒng)計(jì)類的經(jīng)典預(yù)測(cè)方法,，如回歸分析,、時(shí)間序列方法、灰色預(yù)測(cè)方法等,；另一類是人工智能預(yù)測(cè)方法,，例如專家系統(tǒng)和人工神經(jīng)網(wǎng)絡(luò)。隨著人工智能的發(fā)展,，人工神經(jīng)網(wǎng)絡(luò)被廣泛地應(yīng)用在預(yù)測(cè)方面^[2],。目前學(xué)者大多用的是BP神經(jīng)網(wǎng)絡(luò)進(jìn)行負(fù)荷預(yù)測(cè)，是因?yàn)槠溆兄容^強(qiáng)的泛化能力以及非線性映射的能力,，但是在使用過(guò)程中會(huì)發(fā)現(xiàn)它很容易陷入局部最小,，而且收斂的速度比較慢，所以限制了BP神經(jīng)網(wǎng)絡(luò)的發(fā)展,。與BP神經(jīng)網(wǎng)絡(luò)相比,，逐漸發(fā)展的RBF神經(jīng)網(wǎng)絡(luò)避免了BP網(wǎng)絡(luò)的不足，被廣泛應(yīng)用在短期電力負(fù)荷預(yù)測(cè)方面^[3],。

    本文提出的EEMD-SE-GARBF神經(jīng)網(wǎng)絡(luò)組合的預(yù)測(cè)模型主要是通過(guò)EEMD算法自適應(yīng)地對(duì)負(fù)荷序列進(jìn)行分解,，接著結(jié)合樣本熵對(duì)復(fù)雜度相似的子序列進(jìn)行合并，這樣有效減小了運(yùn)算的規(guī)模,。然后,，基于每個(gè)子序列的復(fù)雜度的差異，構(gòu)建相應(yīng)的RBF神經(jīng)網(wǎng)絡(luò)模型,，并通過(guò)遺傳算法優(yōu)化網(wǎng)絡(luò)參數(shù),，避免了神經(jīng)網(wǎng)絡(luò)陷入局部最優(yōu)和收斂性問(wèn)題。最后把每個(gè)新子序列的預(yù)測(cè)結(jié)果相加,，得到最終預(yù)測(cè)值,。

1 EMD和EEMD的原理

1.1 EMD分解法

    經(jīng)驗(yàn)?zāi)B(tài)分解(Empirical Mode Decomposition，EMD)^[4]廣泛應(yīng)用在處理非平穩(wěn)信號(hào)方面,，自適應(yīng)地分解出頻率各不相同的本征模態(tài)函數(shù)(Intristic Model Function,，IMF)分量,，并且每個(gè)IMF分量要符合如下條件：信號(hào)過(guò)零點(diǎn)的個(gè)數(shù)與信號(hào)極大值點(diǎn)、極小值的和相等,，即便不相等也不能超過(guò)一個(gè),；信號(hào)局部最小值、最大值的包絡(luò)均值為零,。

    (1)設(shè)x(t)為原始信號(hào),，找到其最大值點(diǎn)和最小值點(diǎn)，然后用3次樣條曲線方法將其連成曲線,，得到信號(hào)x(t)的上下包絡(luò)線,，計(jì)算兩條包絡(luò)線的均值m₁(t)，進(jìn)而求出信號(hào)x(t)與均值m₁(t)的差值h₁(t)：

1.2 EEMD分解法

    在使用EMD方法時(shí),，如果信號(hào)中有噪聲或信號(hào)中有中斷現(xiàn)象,，這樣就會(huì)產(chǎn)生模態(tài)混疊。集合經(jīng)驗(yàn)?zāi)Ｊ椒纸?Ensemble Empirical Mode Decomposition,，EEMD)是一種基于EMD的改進(jìn)方法^[5-6],，它將高斯白噪聲添加到原始信號(hào)中，然后對(duì)信號(hào)多次EMD算法處理,，可以有效降低模態(tài)混疊程度,。

2 樣本熵

    樣本熵（Sample Entropy，SE）是Richman提出的時(shí)間序列復(fù)雜性測(cè)試方法^[7],。其避免了近似熵的不足,，使近似熵誤差有所降低?？蓞⒖嘉墨I(xiàn)[7]了解樣本熵主要算法,。

    樣本熵的估計(jì)值為：

式中，B^m(t)為任一個(gè)時(shí)間序列與模板匹配的概率,，m代表維數(shù),，r代表閾值，N代表長(zhǎng)度,。SampEn的值與m和r有關(guān),，一般情況下m=1或2，r=0.1SD~0.25SD（SD表示原始信號(hào)x_i的標(biāo)準(zhǔn)差）,，本文m=2,，r=0.2SD。

3 遺傳RBF神經(jīng)網(wǎng)絡(luò)建模

3.1 RBF神經(jīng)網(wǎng)絡(luò)模型

    徑向基函數(shù)(Radical Basis Function,，RBF)神經(jīng)網(wǎng)絡(luò)^[8]具有非線性映射能力較強(qiáng),、網(wǎng)絡(luò)結(jié)構(gòu)簡(jiǎn)單、容錯(cuò)性強(qiáng),、魯棒性強(qiáng)等特點(diǎn),，它可以有效地解決非線性問(wèn)題,，因此被廣泛應(yīng)用在函數(shù)逼近、模式識(shí)別,、時(shí)間序列分析和圖形處理等領(lǐng)域,。

    RBF的網(wǎng)絡(luò)結(jié)構(gòu)如圖1所示。它是一種3層前饋型網(wǎng)絡(luò),，輸入層到隱含層的函數(shù)變換是線性的,，而隱含層到輸出層的函數(shù)變換是非線性的。其中,，隱含層采用的是徑向基函數(shù)^[9],。

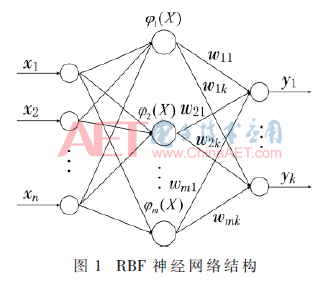
    RBF神經(jīng)網(wǎng)絡(luò)的非線性傳遞函數(shù)采用高斯徑向基函數(shù)，其隱含層的傳遞函數(shù)表示為：

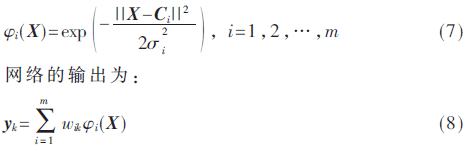
其中,，X∈Rⁿ為n維輸入矢量,，即X=[x₁，x₂,，…，x_n],；C_i表示第i個(gè)基函數(shù)的中心,；σ_i為第i個(gè)非線性變換單元的寬度；||·||通常取歐氏范數(shù),，即||X-C_i||=[(X-C_i)^T(X-C_i)]^1/2,；m為隱含層單元個(gè)數(shù)；w_ik為連接隱含層與輸出層的權(quán)值,。

3.2 RBF神經(jīng)網(wǎng)絡(luò)模型改進(jìn)

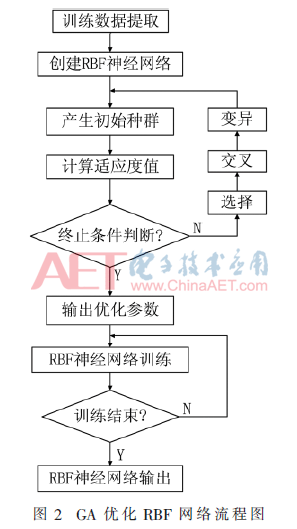
    遺傳算法（Genetic Algorithm,，GA）是一種尋優(yōu)方法，其與神經(jīng)網(wǎng)絡(luò)組合用來(lái)訓(xùn)練網(wǎng)絡(luò)以及優(yōu)化學(xué)習(xí)規(guī)則,。由于神經(jīng)網(wǎng)絡(luò)權(quán)重閾值是隨機(jī)初始化的,，因而容易產(chǎn)生局部最優(yōu)，遺傳算法的全局收斂性不僅可以解決神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)選擇的不確定性問(wèn)題,，而且可以提高網(wǎng)絡(luò)收斂性能,。

    利用遺傳算法對(duì)網(wǎng)絡(luò)的3個(gè)參數(shù)(中心矢量C_i、基寬σ_i和網(wǎng)絡(luò)連接權(quán)值w_ik)進(jìn)行全局尋優(yōu),，保證網(wǎng)絡(luò)的各參數(shù)在全局最優(yōu)范圍內(nèi),。將式(9)作為個(gè)體的適應(yīng)度函數(shù)。

4 基于EMD-SE-GARBF神經(jīng)網(wǎng)絡(luò)的預(yù)測(cè)模型

4.1 模型設(shè)計(jì)

    結(jié)合幾種方法的優(yōu)點(diǎn)建立短期電力負(fù)荷預(yù)測(cè)模型,，模型流程如圖3所示,，具體預(yù)測(cè)流程如下：

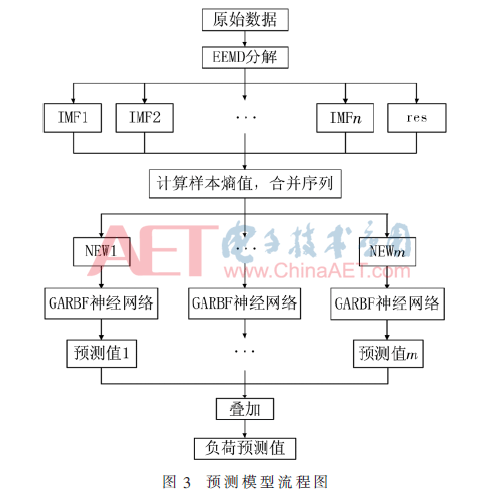
    (1)對(duì)輸入數(shù)據(jù)預(yù)處理，由于輸入變量的單位和取值范圍均不相同,，因此利用式(10)對(duì)數(shù)據(jù)歸一化處理,，取值范圍設(shè)置在[0,，1]。  

式中,，x表示歸一化變量,，x′表示歸一化后的變量，x_max和x_min分別表示變量的最大值和最小值,。

    本文定義工作日為“1”,，休息日為“0”。并對(duì)預(yù)測(cè)日天氣進(jìn)行量化處理,，結(jié)果如表1所示,。

    (2)利用EEMD方法對(duì)負(fù)荷時(shí)間序列進(jìn)行分解，得到各個(gè)IMF分量和一個(gè)剩余分量,。

    (3)計(jì)算各個(gè)子序列的樣本熵值,，將熵值接近的子序列合并成新子序列。

    (4)對(duì)每個(gè)新子序列建立GARBF預(yù)測(cè)模型,。

    (5)利用GA算法對(duì)RBF神經(jīng)網(wǎng)絡(luò)模型進(jìn)行參數(shù)尋優(yōu),，最后得到各新子序列的預(yù)測(cè)值。

    (6)疊加每個(gè)新子序列的預(yù)測(cè)值以獲得最終預(yù)測(cè)值,。

4.2 仿真分析

    為了驗(yàn)證本文提出的短期負(fù)荷預(yù)測(cè)模型EEMD-SE-GARBF的有效性,，使用某大學(xué)活動(dòng)中心的數(shù)據(jù)，對(duì)2018年7月6日24小時(shí)用電負(fù)荷進(jìn)行預(yù)測(cè),，訓(xùn)練樣本為預(yù)測(cè)日前23天的原始數(shù)據(jù),。歷史負(fù)荷數(shù)據(jù)如圖4所示。

    利用EEMD對(duì)歷史負(fù)荷序列進(jìn)行分解,，分解結(jié)果如圖5所示,。可以看出有6個(gè)復(fù)雜度不同的IMF分量和1個(gè)變化比較平緩的剩余分量,，計(jì)算這7個(gè)序列的熵值,，結(jié)果如圖6所示，從圖中可以看出,，序列1和2,，3、4和5,，6和7熵值彼此接近,，將熵值接近的子序列合成新的子序列，新子序列如圖7所示,。

    從圖7中可以看出,，NEW1的波動(dòng)頻率較高，因此它有著非常大的隨機(jī)性，很容易受隨機(jī)因素的影響,。選擇多個(gè)輸入和一個(gè)輸出的RBF網(wǎng)絡(luò),，輸入變量可選為：待測(cè)點(diǎn)前3個(gè)小時(shí)的負(fù)荷值、前一天的負(fù)荷值,、前兩天的負(fù)荷值,、前一周同一時(shí)間的負(fù)荷值、預(yù)測(cè)當(dāng)日的平均溫度,、天氣及日類型,。NEW2幾乎是以日為周期波動(dòng)，隨機(jī)因素對(duì)序列的影響不大,，同樣選擇多個(gè)輸入一個(gè)輸出的RBF網(wǎng)絡(luò),，輸入變量可選為：待測(cè)點(diǎn)前3個(gè)小時(shí)的負(fù)荷值、前一天的負(fù)荷值,、前兩天的負(fù)荷值同一時(shí)間的負(fù)荷值,。NEW3變化相對(duì)穩(wěn)定，周期性不明顯,，選擇一個(gè)多個(gè)輸入多個(gè)輸出網(wǎng)絡(luò),，輸出即為要預(yù)測(cè)的24小時(shí)負(fù)荷值，輸入變量可選為：預(yù)測(cè)日前一天及前一周24小時(shí)的負(fù)荷值,、預(yù)測(cè)當(dāng)日的平均溫度,、天氣及日類型。

    基于上述分析,，為每個(gè)新合成的子序列建立RBF神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型，并將每個(gè)預(yù)測(cè)模型輸出的值相加,，得到最終預(yù)測(cè)值,。

    為驗(yàn)證EEMD-SE-GARBF預(yù)測(cè)模型的有效性，在同樣的計(jì)算條件下分別使用RBF預(yù)測(cè)模型和GARBF預(yù)測(cè)模型對(duì)相同的用電負(fù)荷時(shí)間序列進(jìn)行預(yù)測(cè),，結(jié)果如圖8所示,。

    為了評(píng)判各預(yù)測(cè)模型的精確性，本文采用相對(duì)誤差（RE）和平均絕對(duì)百分比誤差（MAPE）指標(biāo)來(lái)描述預(yù)測(cè)精度,，結(jié)果如圖9和表2所示,。

    通過(guò)分析可知，GARBF預(yù)測(cè)模型MAPE比RBF預(yù)測(cè)模型降低了3.94%,，說(shuō)明使用遺傳算法對(duì)網(wǎng)絡(luò)參數(shù)的優(yōu)化使得預(yù)測(cè)精度有所提高,。從圖9中可以看出，本文中使用的EEMD-SE-GARBF組合預(yù)測(cè)模型相較于其他兩種模型具有相對(duì)平穩(wěn)且較小的相對(duì)誤差,，并且MAPE僅為2.41%,，在預(yù)測(cè)精度上很明顯要高于GARBF預(yù)測(cè)模型和RBF預(yù)測(cè)模型，說(shuō)明在處理具有較強(qiáng)波動(dòng)性的用電負(fù)荷時(shí)間序列中，對(duì)原始數(shù)據(jù)進(jìn)行的平穩(wěn)化預(yù)處理可以有效提高預(yù)測(cè)的精度,。

5 結(jié)論

    本文提出了一種基于EEMD-SE和GARBF神經(jīng)網(wǎng)絡(luò)的組合預(yù)測(cè)方法,，利用EEMD分解法自適應(yīng)地對(duì)負(fù)荷序列進(jìn)行分解，結(jié)合樣本熵對(duì)復(fù)雜度相似的子序列進(jìn)行合并,，并且針對(duì)RBF神經(jīng)網(wǎng)絡(luò)容易陷入局部最優(yōu)問(wèn)題,，利用遺傳算法優(yōu)化網(wǎng)絡(luò)參數(shù)。結(jié)果表明,，所提出的EEMD-SE-GARBF組合預(yù)測(cè)模型可以很好地應(yīng)用于短期電力負(fù)荷預(yù)測(cè),，具有廣泛的應(yīng)用價(jià)值。

參考文獻(xiàn)

[1] 康重慶,，夏青,，劉梅.電力系統(tǒng)負(fù)荷預(yù)測(cè)[M].北京：中國(guó)電力出版社，2007.

[2] 李振華,，許延春,，李龍飛，等.基于BP神經(jīng)網(wǎng)絡(luò)的導(dǎo)水裂隙帶高度預(yù)測(cè)[J].采礦與安全工程學(xué)報(bào),，2015,，32(6)：905-910.

[3] 李龍，魏靖,，黎燦兵.基于人工神經(jīng)網(wǎng)絡(luò)的負(fù)荷模型預(yù)測(cè)[J].電工技術(shù)學(xué)報(bào),，2015，30(8)：225-230.

[4] 楊茂,，陳郁林.基于EMD分解和集對(duì)分析的風(fēng)電功率實(shí)時(shí)預(yù)測(cè)[J].電工技術(shù)學(xué)報(bào),，2016，31(21)：86-93.

[5] 王賀,，胡志堅(jiān),，陳珍，等.基于集合經(jīng)驗(yàn)?zāi)B(tài)分解和小波神經(jīng)網(wǎng)絡(luò)的短期風(fēng)功率組合預(yù)測(cè)[J].電工技術(shù)學(xué)報(bào),，2013,，28(4)：137-144.

[6] 茆美琴，龔文劍,，張榴晨,，等.基于EEMD-SVM方法的光伏電站短期出力預(yù)測(cè)[J].中國(guó)電機(jī)工程學(xué)報(bào)，2013,，33(34)：17-24.

[7] 張學(xué)清,，梁軍，張熙.基于樣本熵和極端學(xué)習(xí)機(jī)的超短期風(fēng)電功率組合預(yù)測(cè)模型[J].中國(guó)電機(jī)工程學(xué)報(bào),，2013,，33(25)：33-40.

[8] 彭顯剛，胡松峰，呂大勇.基于RBF神經(jīng)網(wǎng)絡(luò)的短期負(fù)荷預(yù)測(cè)方法綜述[J].電力系統(tǒng)保護(hù)與控制,，2011,，39(17)：144-148.

[9] 王育飛，付玉超,，孫路.基于混沌-RBF神經(jīng)網(wǎng)絡(luò)的光伏發(fā)電功率超短期預(yù)測(cè)模型[J].電網(wǎng)技術(shù),，2018，42(4)：1110-1116.

作者信息:

高  強(qiáng)1,，2,，李易隆1，2,，李大華1,，2，白梓璇1,，2

（1.天津理工大學(xué) 電氣電子工程學(xué)院 天津市復(fù)雜系統(tǒng)控制理論及應(yīng)用重點(diǎn)實(shí)驗(yàn)室,，天津300384；

2.機(jī)電工程國(guó)家級(jí)實(shí)驗(yàn)教學(xué)示范中心,，天津300384）