1 引言

　　短期負荷預(yù)測是電網(wǎng)經(jīng)濟運行的前提和基礎(chǔ)。準確的負荷預(yù)測結(jié)果,，對電力系統(tǒng)安全可靠運行具有重要意義,。許多學者對此進行了深入研究,，并及時地將數(shù)學上的最新成果應(yīng)用到負荷預(yù)測領(lǐng)域中去，使預(yù)測水平得到提高,，小波網(wǎng)絡(luò)便是基于小波分析理論而構(gòu)成的人工神經(jīng)網(wǎng)絡(luò)模型,，它同時具備了小波變換良好的時頻局部化性質(zhì)和神經(jīng)網(wǎng)絡(luò)的學習能力，它既可以在網(wǎng)絡(luò)結(jié)構(gòu)的確定上有一定的理論指導,，又具有神經(jīng)網(wǎng)絡(luò)的許多優(yōu)秀特性,，并且網(wǎng)絡(luò)的訓練是對特定的凸函數(shù)的優(yōu)化過程，學習速度比一般網(wǎng)絡(luò)要快[3],。
　　研究表明,，小波網(wǎng)絡(luò)比神經(jīng)網(wǎng)絡(luò)使用的基函數(shù)單元更少，具有更快的收斂速度和更高的精度,，然而小波網(wǎng)絡(luò)有兩個明顯的不足：在多維輸入情況下,，學習所用小波基數(shù)目過多，其次是隨著網(wǎng)絡(luò)輸入維數(shù)的增大,，使得小波網(wǎng)絡(luò)的收斂速度大大下降,，即不能夠解決所謂的“維數(shù)災(zāi)”問題[5]。由于影響電力系統(tǒng)短期負荷預(yù)測的因素諸多,，本身也是一個多維輸入問題,，基于此，本文提出了一種將小波網(wǎng)絡(luò)和模糊神經(jīng)網(wǎng)絡(luò)相結(jié)合的短期負荷預(yù)測的新方法,，利用一組模糊規(guī)則將小波網(wǎng)絡(luò)分為若干小波子網(wǎng)絡(luò),，每條模糊規(guī)則前提部分將輸入樣本空間劃分為一個局部子空間，其結(jié)論部分則對應(yīng)某一特定尺度下的小波子網(wǎng)絡(luò),，不同尺度下的小波子網(wǎng)絡(luò)用于捕捉信號的各種不同特性,，將其進行線性組合來逼近信號。它在保證選擇一定數(shù)量的小波基函數(shù)下,，由隸屬度函數(shù)和小波子網(wǎng)絡(luò)的輸出來精確確定整個網(wǎng)絡(luò)的輸出,，使網(wǎng)絡(luò)到達最佳逼近，同時簡化了網(wǎng)絡(luò)的結(jié)構(gòu),，避免了小波網(wǎng)絡(luò)的“維數(shù)災(zāi)”問題,，提高了計算效率,。實踐證明該方法具有較高的精度和很強的泛化能力,。

2 小波網(wǎng)絡(luò)
　　 對于輸入X=[x1,x2,...xq] ，定義其多維小波母函數(shù)為[5]：
　
    由小波分析理論知,，任一能量有限的信號都有如下離散小波分解形式[2]：
　
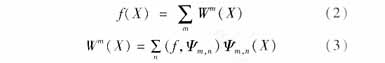
其中：Wm（X）為尺度層m上的小波分量,，n是尺度層m上的小波函數(shù)的平移因子。
　　從式（2）,、（3）中不難看出任一信號f(X)都可以分解成在不同尺度層上小波分量的線性組合,，這正是我們提出FWN(模糊小波網(wǎng)絡(luò))的出發(fā)點,。
　　從理論上來說，信號的小波展開式的基有無窮多個,，而在分析電力負荷頻譜特性時發(fā)現(xiàn),，負荷信號的變化過程具有連續(xù)頻譜的特性[4]，負荷預(yù)測僅涉及一個頻帶,，故只需選擇最能代表信號信息的主頻段來逼近信號,。因此在一定精度要求下總可以截取有限小波函數(shù)作為基函數(shù)，得：
　
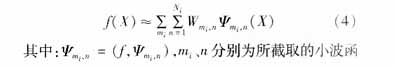
數(shù)的尺度及平移因子,。這樣就可以用一個以小波函數(shù)作為激活函數(shù),、wmi,n作為從隱含層到輸出層的權(quán)值的小波神經(jīng)網(wǎng)絡(luò)來表示信號f(X)∈L2R。在本文所采用的FWN中,，為了避免多維小波網(wǎng)絡(luò)的“維數(shù)災(zāi)”問題,，采用了若干小波子網(wǎng)絡(luò)，每一小波子網(wǎng)絡(luò)表示在同一尺度層上的小波分量的線性組合,，從而使復雜問題簡單化,，達到分而治之，結(jié)合模糊神經(jīng)網(wǎng)絡(luò)將各小波子網(wǎng)絡(luò)進行線性組合,，來逼近信號f(X),，一小波子網(wǎng)絡(luò)的結(jié)構(gòu)如下圖1。

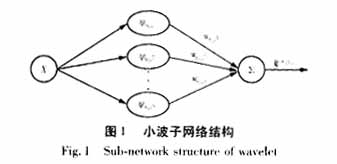
　　由小波理論的多分辨率分析可知,，粗尺度層上的小波網(wǎng)絡(luò)用于捕獲信號的全局信息,，而較細尺度層上的小波網(wǎng)絡(luò)用于捕捉信號的各種局部信息，使FWN網(wǎng)絡(luò)具有明確的物理意義,，每一小波子網(wǎng)絡(luò)的規(guī)模大大簡化,，易于進行訓練，提高了計算效率的同時也提高了預(yù)測精度,。

3 模糊小波網(wǎng)絡(luò)結(jié)構(gòu)
　　本文采用由Takigi-Sugeno改進的模糊推理方法[5],，假定模糊系統(tǒng)有q個輸入，單個輸出其模糊規(guī)則有著如下形式：
 
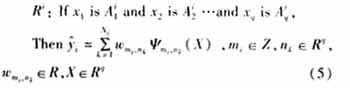
其中,，Ri表示第i(1≤i≤c)條模糊規(guī)則,；Xj(1≤j≤q)為輸入集X中的第個變量；Ni表示第i條模糊規(guī)則中選用的小波基總數(shù),；nk=[n1k,n2k,...,nqk]為平移因子,；而則是第i條模糊規(guī)則的輸出，其值為具有相同尺度因子2mi小波基的線性組合,，本文用一個小波子網(wǎng)絡(luò)表示,；模糊子Aij集用隸屬度函數(shù) 
  
    由模糊推理層得到每條模糊規(guī)則對于輸入X的適用度μi(X)，實現(xiàn)歸一算法得到其激活度，它主要是決定了每個小波子網(wǎng)絡(luò)的輸出在整個網(wǎng)絡(luò)輸出中所占的比重：
 
 
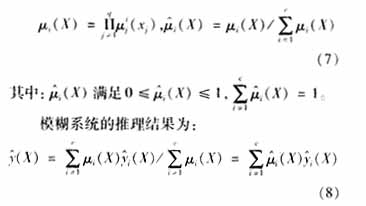
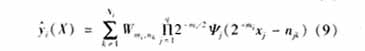
    在改進的Takigi-Sugeno模糊神經(jīng)網(wǎng)絡(luò)和小波網(wǎng)絡(luò)的基礎(chǔ)上,，式(5)－(8)所描述的FWN可以用一個多層網(wǎng)絡(luò)來實現(xiàn),，如上圖2中所示.

    該FWN由常規(guī)的四層模糊神經(jīng)網(wǎng)絡(luò)組成，分別為：輸入層,、隸屬度函數(shù)生成層,、推理層及反模糊化層，各層神經(jīng)元數(shù)目分別為q,，q×c,，和c+1，所以一旦確定輸入個數(shù)和模糊規(guī)則數(shù),，模糊小波網(wǎng)絡(luò)的結(jié)構(gòu)也就確定了,，WNNi表示第i個小波子網(wǎng)絡(luò)。在隸屬度函數(shù)生成層中所采用的激活函數(shù)是式(6)中給出的高斯型隸屬度函數(shù),。
    本文中采用的FWN模型與常規(guī)的模糊神經(jīng)網(wǎng)絡(luò)模型最大的區(qū)別就在于反模糊化層的不同,，在模糊神經(jīng)網(wǎng)絡(luò)中只能對信號進行局部化逼近，而FWN中則采用了一系列小波子網(wǎng)絡(luò),，它既能對信號進行全局逼近,，也能進行局部逼近，而且對于確定模糊規(guī)則數(shù)有合理的依據(jù),，正因為此,，F(xiàn)WN具有更好的信號逼近能力和更強的適應(yīng)力。

4 模糊小波網(wǎng)絡(luò)的學習算法
    給定L個訓練樣本對,，Xl(l=1,2,...,L)表示第l個訓練樣本的輸入,，分別表示網(wǎng)絡(luò)的實際輸出和目標輸出。求解FWN的參數(shù)采用使之間誤差最小的BP算法,，其流程如下：
  
 
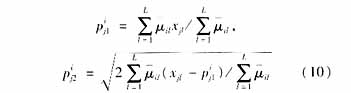
    （3）讀入訓練樣本對,，計算網(wǎng)絡(luò)輸出，并計算訓練誤差：若滿足精度要求,，則跳轉(zhuǎn)到（5）,，否則繼續(xù)；
 
 
式中:η,、a分別是學習速率和慣性常數(shù),。跳轉(zhuǎn)至（3）.
    （5）獲得網(wǎng)絡(luò)參數(shù)訓練過程結(jié)束。

5 算例分析
    為了驗證方法的可行性和有效性,，本文以某市電力系統(tǒng)實際歷史負荷為例,，用上述FWN模型進行短期負荷預(yù)測仿真。
    選取模型的輸入量有22個,，分別是待測日和待測日前一天的最高溫度,、最低溫度,、濕度和天氣狀況,；待測日前一天的最大,、最小及平均負荷；待測日前一天及前兩天分別以預(yù)測時段為中心取五個負荷值,，待測日前一周預(yù)測時段的負荷值,。輸出量有1個為待測日某時段的負荷值，本文采取的是逐點預(yù)測,。利用待測日前六周的歷史數(shù)據(jù)來訓練網(wǎng)絡(luò),。其中學習速率η＝0.25，慣性常數(shù)a＝0.6,，學習誤差E=0.0005%,，尺度mi取6個值(mi=-1,0,1,2,3,4)，分別為－1到4,，也即是有6條模糊規(guī)則,。為了比較模型優(yōu)劣，在選擇相同的訓練模式,、學習速率和慣性常量下,，采用人工神經(jīng)網(wǎng)絡(luò)來模型進行負荷預(yù)測，取預(yù)報日為2001年6月7日(正常日),，其預(yù)測結(jié)果如表1,，同時還給出了負荷變化最大、溫度和天氣狀況變化最劇烈?guī)兹盏念A(yù)測結(jié)果,，如表2,。

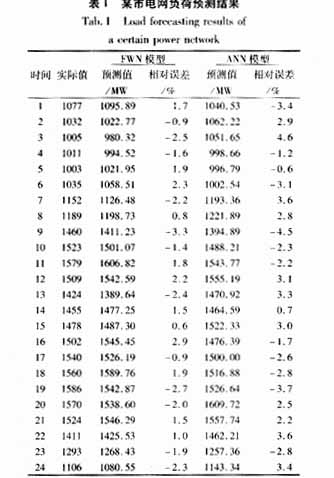
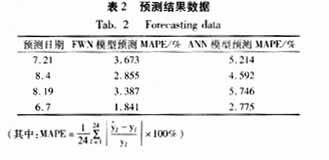
    從預(yù)測結(jié)果我們可以看出，基于模糊小波網(wǎng)絡(luò)的負荷預(yù)測精度得到顯著提高,，同時也證明這種方法是完全可行的,。從表1中還可以發(fā)現(xiàn)模糊小波網(wǎng)絡(luò)的預(yù)測相對誤差變化很均勻，表明其泛化能力比神經(jīng)網(wǎng)絡(luò)大有提高,。從表2中可以看出模糊小波網(wǎng)絡(luò)能夠更好地擬合負荷與天氣因素之間的密切關(guān)系,，進行更加可靠的預(yù)測。

6 結(jié)論
    由于電力系統(tǒng)日益龐大,，各個方面因素的影響使得負荷變化的不確定性增加,，這也加大了負荷預(yù)測的難度。近年來,，許多電力工作者也提出了各種負荷預(yù)測模型,，其中小波網(wǎng)絡(luò)便是近年來結(jié)合小波變換與人工神經(jīng)網(wǎng)絡(luò)思想而形成的一種數(shù)學建模方法，研究表明小波網(wǎng)絡(luò)的預(yù)測精度和計算速度比普通神經(jīng)網(wǎng)絡(luò)有較大提高,，但是小波網(wǎng)絡(luò)的缺點是一般只適合低維情況,，而且為了達到更高的預(yù)測精度需要較多的小波函數(shù)，為了有效的處理高維問題的不足，本文提出了一種新穎的基于模糊小波網(wǎng)絡(luò)的短期負荷預(yù)測模型,，這種FWN模型將小波網(wǎng)絡(luò)和模糊神經(jīng)網(wǎng)絡(luò)有機結(jié)合起來,，利用一組模糊規(guī)則，采用一組小波子網(wǎng)絡(luò)的結(jié)構(gòu)模型,，使得小波子網(wǎng)絡(luò)的隱層規(guī)模大大降低,，避免了小波網(wǎng)絡(luò)的“維數(shù)災(zāi)”問題，提高了運算效率,，通過同時調(diào)整小波函數(shù)的位移因子和隸屬度函數(shù)的形狀,，可以達到全局最優(yōu)的擬合效果，從而有效地提高了預(yù)測精度,。通過大量仿真計算表明,，該方法是可行且有效的，同時本文為小波網(wǎng)絡(luò)在電力系統(tǒng)負荷預(yù)測中的應(yīng)用做出了進一步探索研究,。