0 引言

    編碼技術(shù)作為信息通信技術(shù)的重要組成部分，集成了計(jì)算機(jī)技術(shù),、數(shù)學(xué)理論等多學(xué)科的特點(diǎn),。糾錯(cuò)碼是編碼領(lǐng)域的重要研究?jī)?nèi)容，自從20世紀(jì)90年代提出渦輪(turbo)碼和低密度奇偶校驗(yàn)(LDPC)碼,，糾錯(cuò)碼技術(shù)的發(fā)展取得了突破性的進(jìn)展,，帶動(dòng)整個(gè)通信技術(shù)質(zhì)的飛躍。

    類turbo(turbo-like)碼是turbo碼和LDPC碼的共同子集,，集成了turbo碼編碼簡(jiǎn)單,、LDPC碼譯碼簡(jiǎn)單等優(yōu)點(diǎn)，成為糾錯(cuò)碼技術(shù)的一個(gè)研究熱點(diǎn),。重復(fù)累積(Repeat Accumulate,，RA)碼是一類最簡(jiǎn)單的類Turbo碼，由DIVSALAR D于1998年提出^[1],。它是一類碼率為1/q的串行級(jí)聯(lián)碼(Serially Concatenated Codes,，SCC)。雖然構(gòu)造簡(jiǎn)單,，但RA碼的迭代譯碼性能非常好,。文獻(xiàn)[1]-[2]證明，對(duì)于AWGN信道,，碼率R→0時(shí),，RA碼理論計(jì)算能夠?qū)崿F(xiàn)香農(nóng)極限(Shannon limit)-1.592 dB。文獻(xiàn)[3]-[4]提出了非規(guī)則重復(fù)累積(Irregular Repeat Accumulate,，IRA)碼,，并詳細(xì)分析了IRA碼性能，證明IRA碼具有很好的譯碼性能,，也引起人們?cè)絹?lái)越多地研究碼^[5-6],，它具有線性時(shí)間編碼復(fù)雜度，其譯碼性能也很突出。級(jí)聯(lián)樹(shù)(Concatenated Tree,，CT)碼是另一類結(jié)構(gòu)簡(jiǎn)單的類Turbo碼,，由香港城市大學(xué)的李坪博士于2001年提出，它由M個(gè)兩狀態(tài)網(wǎng)格碼通過(guò)交織器連接在一起^[7],。CT碼具有樹(shù)結(jié)構(gòu),，包含遞歸信息比特和非遞歸信息比特兩個(gè)部分，其譯碼算法簡(jiǎn)單,，性能與RA碼相當(dāng),。傳統(tǒng)的編碼理論通過(guò)距離特性分析譯碼的糾錯(cuò)性能，而采用軟判決的迭代譯碼的糾錯(cuò)性能是隨著迭代次數(shù)的增加而漸進(jìn)體現(xiàn)的,，密度進(jìn)化方法^[8]就是分析這種漸進(jìn)性能的重要工具,。

    本文首先由RA碼和CT碼的特點(diǎn)得到啟發(fā)，提出了一種新型信道編碼方案ART碼,；之后,，分析了編碼結(jié)構(gòu)，用并行級(jí)聯(lián)分量樹(shù)碼的遞歸信息和非遞歸信息結(jié)構(gòu)取代串行級(jí)聯(lián)RA碼的分量累加碼,，并前置累加器,，作為預(yù)編碼器；研究了譯碼方案,，根據(jù)密度進(jìn)化方法推導(dǎo)了AWGN信道下適合ART碼的高斯近似算法,；最后，給出了ART碼的性能分析和高斯信道,、瑞利信道譯碼仿真結(jié)果,。理論分析和仿真結(jié)果表明，改進(jìn)編碼能夠獲得較大編碼增益,，同時(shí)具有較好譯碼性能,。

1 ART碼結(jié)構(gòu)與譯碼

1.1 ART碼結(jié)構(gòu)

    如圖1所示，ART碼采用SCC編碼結(jié)構(gòu),。與RA碼相比,，在重復(fù)碼前面加了一個(gè)累加器以及刪余，同時(shí)用CT碼中的分量樹(shù)碼代替交織器后面的累加器,。

    這樣的改變是有意義的,，前面的累加器可以看作一個(gè)碼率為1、傳遞函數(shù)為1/(1+D)的“預(yù)編碼器”,，刪余用來(lái)提高碼率,，文獻(xiàn)[9]、[10]的研究表明這種結(jié)構(gòu)可以獲得更高的編碼增益,，如圖2所示,。

    樹(shù)碼編碼器用來(lái)產(chǎn)生CT碼的分量碼,，CT碼是并行級(jí)聯(lián)碼(Parallel Concatenated Codes，PCC)結(jié)構(gòu),，眾所周知PCC結(jié)構(gòu)存在“地板效應(yīng)”,，并且存在收斂問(wèn)題^[11-12]，而ART碼的SCC結(jié)構(gòu)則很好地解決了這些問(wèn)題,。圖3給出系統(tǒng)樹(shù)碼貝葉斯網(wǎng)絡(luò)圖。

    根據(jù)圖3的貝葉斯網(wǎng)絡(luò)圖,，分別記節(jié)點(diǎn)的遞歸信息比特和非遞歸信息比特為s_r和s_nr,，刪余奇偶比特和非刪余奇偶比特為p_p和p_np，則有：

其中,，J_r為節(jié)點(diǎn)的遞歸信息比特?cái)?shù),，J_nr為節(jié)點(diǎn)的非遞歸信息比特?cái)?shù)。

1.2 迭代譯碼算法

    ART碼可以采用并行置信傳播迭代譯碼算法(Belief-Propagation,，BP)^[13-14]和串行turbo譯碼算法^[15],。通常，串行譯碼收斂速度較快,，但復(fù)雜度高,；而B(niǎo)P迭代譯碼算法只在相鄰節(jié)點(diǎn)間產(chǎn)生信息交換，因此易于實(shí)現(xiàn)高速并行譯碼,，其復(fù)雜度遠(yuǎn)低于turbo譯碼算法,。因此，采用BP算法對(duì)ART碼進(jìn)行譯碼,。

    圖4給出ART碼的Tanner圖表示,。可以看出它包含3部分：信息節(jié)點(diǎn)S,、校驗(yàn)節(jié)點(diǎn)C和奇偶節(jié)點(diǎn)P,。其中，S和P構(gòu)成變量節(jié)點(diǎn)V,。消息在V和C之間傳遞,，由此實(shí)現(xiàn)BP迭代譯碼算法。

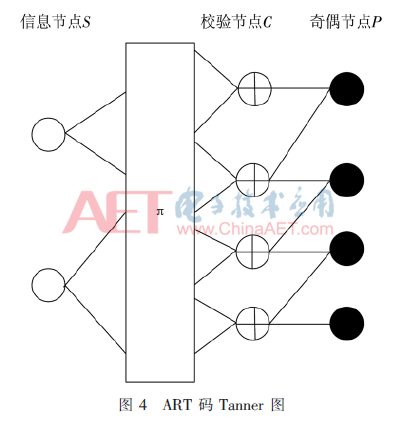
    用對(duì)數(shù)似然比(Log-Likelihood Ratio,，LLR)形式L(x)來(lái)表示所有消息的傳遞,，即L(x)=ln[P(x=0)/(x=1)]。

2 密度進(jìn)化分析

2.1  ART碼密度進(jìn)化算法原理

    密度進(jìn)化是分析迭代譯碼性能的重要工具,，通過(guò)密度進(jìn)化得到的門限值σ^*是ART碼在給定碼率R條件下能夠成功譯碼的最佳信道參數(shù),。

    由前述譯碼算法和式(6)～式(8)，可以得到第l次迭代更新過(guò)程為：

2.2 ART碼高斯近似算法

    用上述近似算法得到的門限值如表1所示,。給定條件q=4,，分別選取不同比例的J_r和J_nr,。 

3 基于ART編碼的OFDM無(wú)線應(yīng)用方案

    可將ART碼方案應(yīng)用于OFDM調(diào)制系統(tǒng)，給出一個(gè)完整的ART-OFDM無(wú)線系統(tǒng)鏈路傳輸系統(tǒng),，如圖5所示,。

    設(shè)OFDM子載波數(shù)為N，則ART編碼矢量映射到OFDM的N個(gè)不同子載波上,，經(jīng)過(guò)對(duì)ART編碼序列的一系列處理,，調(diào)制生成ART-OFDM時(shí)域抽樣信號(hào)序列，這個(gè)OFDM已調(diào)信號(hào)具有較強(qiáng)的抗符號(hào)間干擾和載波間干擾能力^[10],。

4 仿真分析

    根據(jù)以上分析,，分別在ART碼(J_r，J_nr)為(3,，1)和(2,，2)時(shí)進(jìn)行BER性能仿真，碼率R=1/2,。仿真條件分別為AWGN信道和瑞利信道,，BPSK調(diào)制，數(shù)據(jù)長(zhǎng)度分別為N₁=1 024和N₂=5 120,，迭代次數(shù)L=18,。圖6、圖7給出了仿真結(jié)果,，同時(shí)給出碼率R=1/2刪余RA(4)碼性能曲線,，仿真條件與ART碼相同。

    從圖6,、圖7中可以看出,，兩種信道條件下，數(shù)據(jù)長(zhǎng)度N₁=1 024和N₂=5 120時(shí)的ART碼性能均明顯優(yōu)于相同碼率刪余RA碼,，性能優(yōu)劣排序?yàn)椋? 120長(zhǎng)度ART碼優(yōu)于5 120長(zhǎng)度刪余RA碼,，優(yōu)于1 024長(zhǎng)度ART碼，優(yōu)于1 024長(zhǎng)度刪余RA碼,；并且,，當(dāng)SNR較小時(shí)，ART(3,，1)碼與ART(2,，2)碼性能比較接近，隨著SNR的增大,，ART(3,，1)碼的性能略優(yōu)于ART(2，2)碼,，仿真結(jié)果與前面的密度進(jìn)化分析結(jié)果大致相同,。

    根據(jù)前述ART-OFDM編碼調(diào)制方案,，分別在瑞利信道和多徑信道進(jìn)行性能仿真，設(shè)置參數(shù)為：交織長(zhǎng)度N=1 024,，迭代次數(shù)L=20,，基帶信號(hào)BPSK調(diào)制，子載波數(shù)/計(jì)算點(diǎn)數(shù)點(diǎn)IFFT=64點(diǎn),，Jakes=6徑模型,，且各徑子信道為平坦瑞利衰落，同樣采用ART(3,，1)碼和ART(2,，2)碼，并給出1/2碼率刪余RA(4)碼性能作為參考,，圖8、圖9為仿真結(jié)果,。

    從圖8,、圖9中可以看出，無(wú)論瑞利平坦衰落信道還是多徑衰落信道,，ART-COFDM系統(tǒng)都具有較好的譯碼性能,，其性能變化曲線與圖6、圖7的BER性能曲線變化趨勢(shì)類似,，ART碼性能優(yōu)于RA碼,，并且，兩種ART碼性能相近,，隨著SNR的增大,，ART(3，1)碼性能最優(yōu),。

5 結(jié)束語(yǔ)

    本文提出一種改進(jìn)累積重復(fù)樹(shù)碼（ART碼）方案,，研究了ART碼的編碼過(guò)程和BP迭代譯碼算法，采用前置累加器結(jié)構(gòu)提高了編碼增益,，采用串行級(jí)聯(lián)碼SCC結(jié)構(gòu)將分量樹(shù)碼直接與交織器相連,，避免了并行級(jí)聯(lián)碼PCC結(jié)構(gòu)的地板效應(yīng)，從而提高了譯碼增益,；分析了ART碼高斯密度進(jìn)化算法,，得出了ART（4）碼在不同條件下的譯碼門限值；研究了基于ART編碼的COFDM系統(tǒng)結(jié)構(gòu),，并以此為基礎(chǔ)討論了ART碼與OFDM調(diào)制相結(jié)合的無(wú)線網(wǎng)絡(luò)傳輸應(yīng)用結(jié)構(gòu)框圖,。理論分析和仿真均顯示，無(wú)論在AWGN信道還是衰落信道,，以及基于ART碼架構(gòu)的COFDM系統(tǒng),，ART碼均具有較好譯碼性能,；并且，ART(3,，1)碼和ART(2,，2)碼性能基本相當(dāng)，當(dāng)信噪比SNR較小時(shí),，ART(2,，2)碼性能略好于ART(3，1)碼,，隨著SNR的增大,，ART(3，1)碼性能最優(yōu),。

    本文的研究表明,，ART碼改進(jìn)了傳統(tǒng)RA碼結(jié)構(gòu)，其具有編譯碼結(jié)構(gòu)比較簡(jiǎn)單,，譯碼性能較RA碼更好的特點(diǎn),，采用ART碼的OFDM系統(tǒng)相較RA碼OFDM系統(tǒng)，可以更好地抵抗無(wú)線信道噪聲和衰落干擾,，提高了無(wú)線網(wǎng)絡(luò)傳輸系統(tǒng)可靠性,。對(duì)ART碼譯碼復(fù)雜度和更多應(yīng)用等問(wèn)題，仍有待進(jìn)一步研究論證,。

參考文獻(xiàn)

[1] DIVSALAR D,，JIN H，MCELIECE R.Coding theorems for Turbo-like codes[C].AC1998.Monticello：IEEE Press,，1998：201-210.

[2] 張忠培,，史治平，王傳丹.現(xiàn)代編碼理論與應(yīng)用[M].北京：國(guó)防工業(yè)出版社,，2007.

[3] JIN H,，KHANDEKAR A，MCELIECE R.Irregular repeataccumulate codes[C].ISTC2000.Brest：IEEE Press,，2000：1-8.

[4] 張睿.重復(fù)累積碼的性能與優(yōu)化設(shè)計(jì)[D].西安：西安電子科技大學(xué),，2013.

[5] 彭立，張琦,，王渤.針對(duì)IRA-LDPC碼類的半隨機(jī)半代數(shù)結(jié)構(gòu)設(shè)計(jì)[J].通信學(xué)報(bào),，2014，35(3)：77-84.

[6] 貴文麗.基于重復(fù)累積結(jié)構(gòu)的高性能噴泉碼研究[D].西安：西安電子科技大學(xué),，2017.

[7] Li Ping,，Wu Keying.Concatenated tree codes：a low-com-plexity, high-performance approach[J].IEEE Transactions on Information Theory，2001,，47(2)：791-799.

[8] RICHARDSON T J,，URBANKE R L.The capacity of low-density parity-check codes under message-passing decoding[J].IEEE Transactions on Information Theory,，2001，47(2)：599-618.

[9] ABBASFAR A,，DIVSALAR D,，YAO K.Accumulate-repeataccumulate codes[J].IEEE Transactions on Communications，2007,，55(4)：692-702.

[10] 楊茂繁.累積重復(fù)樹(shù)碼及其在OFDM系統(tǒng)中的性能研究[D].北京：北京郵電大學(xué),，2011.

[11] DIVSALAR D，POLLARA F.Multiple turbo codes[C].MILCOM1995.San Diego：IEEE Press,，1995：5-8.

[12] 栗嘉若.基于QC-LDPC的CO-OFDM系統(tǒng)編碼算法研究[D].長(zhǎng)春：吉林大學(xué),，2017.

[13] 褚楚.LDPC碼譯碼機(jī)制及其在秘鑰協(xié)議商中的應(yīng)用[D].南京：南京郵電大學(xué)，2017.

[14] 周麗靜.QC-LDPC碼校驗(yàn)矩陣的構(gòu)造和譯碼算法的研究[D].沈陽(yáng)：東北大學(xué),，2015.

[15] 東夢(mèng)楠.LDPC碼的編譯碼及其在5G系統(tǒng)中的應(yīng)用研究[D].北京：北京郵電大學(xué),，2018.

[16] CHUNG S Y，RICHARDSON T J,，URBANKE R L.Analysis of sum-product decoding of low-density parity-check codes using a gaussian approximation[J].IEEE Transactions on Information Theory,，2001，47(2)：657-670.

作者信息:

耿  珂1,，寧兆成2，劉  軍2,，楊茂繁3,，高  強(qiáng)1，熊華鋼1

(1.北京航空航天大學(xué),，北京100191,；2.東北大學(xué)，遼寧 沈陽(yáng)110819,；3.中國(guó)人民解放軍93303部隊(duì),，遼寧 沈陽(yáng)110015)