隨著信息時(shí)代的到來,，數(shù)字信號處理已經(jīng)成為當(dāng)今一門極其重要的學(xué)科和技術(shù)，并且在通信,、語音,、圖像,、自動(dòng)控制等眾多領(lǐng)域得到了廣泛的應(yīng)用。在數(shù)字信號處理中,，數(shù)字濾波器" title="數(shù)字濾波器">數(shù)字濾波器占有極其重要的地位,，它具有精度高、可靠性好,、靈活性大等特點(diǎn)?，F(xiàn)代數(shù)字濾波器可以用軟件或硬件兩種方式來實(shí)現(xiàn)。軟件方式實(shí)現(xiàn)的優(yōu)點(diǎn)是可以通過濾波器參數(shù)的改變?nèi)フ{(diào)整濾波器的性能,。
　　MATLAB是一種面向科學(xué)和工程計(jì)算的語言,，它集數(shù)值分析、矩陣運(yùn)算,、信號處理和圖形顯示于一體,，具有編程效率高、調(diào)試手段豐富,、擴(kuò)充能力強(qiáng)等特點(diǎn),。MATLAB的信號處理工具箱具有強(qiáng)大的函數(shù)功能，它不僅可以用來設(shè)計(jì)數(shù)字濾波器,，還可以使設(shè)計(jì)達(dá)到最憂化,，是數(shù)字濾波器設(shè)計(jì)的強(qiáng)有力工具。
1 FIR濾波器的設(shè)計(jì)
1.1 FIR濾波器簡介^[1]
　　根據(jù)沖激響應(yīng)的時(shí)域特性,，數(shù)字濾波器可分為無限長沖激響應(yīng)濾波器（IIR）和有限長沖激響應(yīng)濾波器（FIR）,。FIR的突出優(yōu)點(diǎn)是：系統(tǒng)總是穩(wěn)定的、易于實(shí)現(xiàn)線性相位,、允許設(shè)計(jì)多通帶（或多阻帶）濾波器,，但與IIR相比，在滿足同樣阻帶衰減的情況下需要的階數(shù)較高,。濾波器的階數(shù)越高,，占用的運(yùn)算時(shí)間越多，因此在滿足指標(biāo)要求的情況下應(yīng)盡量減少濾波器的階數(shù),。
　　FIR濾波器的基本結(jié)構(gòu)可以理解為一個(gè)分節(jié)的延時(shí)線,，把每一節(jié)的輸出加權(quán)累加，可得到濾波器的輸出,。FIR濾波器的沖激響應(yīng)h(n)是有限長的,，數(shù)學(xué)上M階FIR濾波器可以表示為：
　　
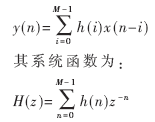
　　FIR濾波器的設(shè)計(jì)問題實(shí)質(zhì)上是確定能滿足所要求的轉(zhuǎn)移序列或脈沖響應(yīng)" title="脈沖響應(yīng)">脈沖響應(yīng)的常數(shù)的問題，設(shè)計(jì)方法主要有窗函數(shù)法,、頻率采樣法和等波紋最佳逼近法等,。
1.2 窗函數(shù)設(shè)計(jì)法的步驟^[3][4]
　　窗函數(shù)設(shè)計(jì)法是一種通過截短和計(jì)權(quán)的方法使無限長非因果序列成為有限長脈沖響應(yīng)序列的設(shè)計(jì)方法。通常在設(shè)計(jì)濾波器之前,，應(yīng)該先根據(jù)具體的工程應(yīng)用確定濾波器的技術(shù)指標(biāo),。在大多數(shù)實(shí)際應(yīng)用中,，數(shù)字濾波器常常被用來實(shí)現(xiàn)選頻操作，所以指標(biāo)的形式一般為在頻域中以分貝值給出的相對幅度響應(yīng)和相位響應(yīng),。
　　用窗函數(shù)法設(shè)計(jì)FIR濾波器的步驟如下：
　?。?）根據(jù)過渡帶寬及阻帶衰減要求，選擇窗函數(shù)的類型并估計(jì)窗口長度N（或階數(shù)M=N-1）,。窗函數(shù)類型可根據(jù)最小阻帶衰減AS獨(dú)立選擇,，因?yàn)榇翱陂L度N對最小阻帶衰減A_S沒有影響。在確定窗函數(shù)類型以后,，可根據(jù)過渡帶寬小于給定指標(biāo)確定所擬用的窗函數(shù)的窗口長度N,。設(shè)待求濾波器的過渡帶寬為△ω，它與窗口長度N近似成反比,。窗函數(shù)類型確定后,，其計(jì)算公式也確定了，不過這些公式是近似的,，得出的窗口長度還要在計(jì)算中逐步修正,。原則是在保證阻帶衰減滿足要求的情況下，盡量選擇較小的N,。在N和窗函數(shù)類型確定后,，即可調(diào)用MATLAB中的窗函數(shù)求出" title="求出">求出窗函數(shù)w_d(n)。
　?。?）根據(jù)待求濾波器的理想頻率響應(yīng)求出理想單位脈沖響應(yīng)hd(n),。如果給出待求濾波器的頻率響應(yīng)為H_d(e^jω)，則理想的單位脈沖響應(yīng)可以用下面的傅里葉反變換式求出：
　　
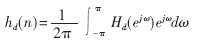
　　在一般情況下,，h_d(n)是不能用封閉公式表示的,，需要采用數(shù)值方法表示。從ω=0到ω=2π采樣N點(diǎn),，采用離散傅里葉反變換(IDFT)即可求出,。
　　（3）計(jì)算濾波器的單位脈沖響應(yīng)h(n),。它是理想單位脈沖響應(yīng)和窗函數(shù)的乘積,，即h(n)=h_d(n)·w_d(n)，在MATLAB中用點(diǎn)乘命令表示為h=hd·wd,。
　?。?）驗(yàn)算技術(shù)指標(biāo)是否滿足要求。為了計(jì)算數(shù)字濾波器在頻域中的特性,，可調(diào)用freqz子程序,，如果不滿足要求，可根據(jù)具體情況，調(diào)整窗函數(shù)類型或長度,，直到滿足要求為止。
　　使用窗函數(shù)法設(shè)計(jì)時(shí)要滿足以下兩個(gè)條件：
　?。?）窗譜主瓣盡可能地窄,，以獲得較陡的過渡帶；
　?。?）盡量減少窗譜的最大旁瓣的相對幅度,，也就是使能量盡量集中于主瓣，減小峰肩和紋波,，進(jìn)而增加阻帶的衰減,。
　　根據(jù)工程經(jīng)驗(yàn)，給定的濾波器指標(biāo)參數(shù)一般為通帶截止頻率" title="截止頻率">截止頻率ω_p,、阻帶截止頻率ω_s,、實(shí)際通帶波動(dòng)R_p和最小阻帶衰減A_s。窗函數(shù)設(shè)計(jì)的經(jīng)驗(yàn)公式為：
　　
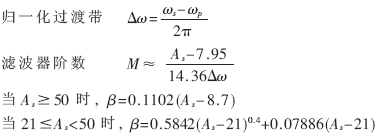
　　在實(shí)際工程中常用的窗函數(shù)有五種,，即矩形窗,、三角窗、漢寧窗,、海明窗和凱澤窗,。這些窗函數(shù)在MATLAB中分別用boxcar、triang,、hanning,、hamming、kaiser實(shí)現(xiàn),，它們之間的性能比較如表1所示,。

2 MATLAB環(huán)境下的設(shè)計(jì)實(shí)例^[2][4]
2．1 高通濾波器的設(shè)計(jì)
　　用窗函數(shù)設(shè)計(jì)高通濾波器，性能指標(biāo)如下：通帶截止頻率ω_s=0.2π,，阻帶截止頻率ω_p=0.3π,，實(shí)際通帶波動(dòng)R_p=0.25dB,最小阻帶衰減A_s=70dB。
　　分析：從表1可以看出凱澤窗能提供74dB的最小阻帶衰減,，所以選用凱澤窗進(jìn)行設(shè)計(jì),，程序主要部分如下：
　　As=70;
　　ωs=0.2*π;
　　ωp=0.3*π
　　tr_width=ωp-ωs;　　　　　　　　　　　　　　　　%計(jì)算過渡帶寬
　　M=ceil((As-7.95)*2*π/(14.36*tr_width)+1)+1;　　　 %按凱澤窗計(jì)算濾波器長度
　　disp([’濾波器的長度為’,num2str(M)]);
　　beta=0.1102*(As-8.7); %計(jì)算凱澤窗的β值
　　n=[0:1:M-1];
　　disp([’線性相位斜率為’,num2str(beta)]);
　　　　w_kai=(kaiser(M,beta))’; %求凱澤窗函數(shù)
　　　　ωc=(ωs+ωp)/2;
　　　　hd=ideal_lp(π,M)-ideal_lp(ωc,M); %求理想脈沖響應(yīng)
　　　　h=hd.*w_kai; %設(shè)計(jì)的脈沖響應(yīng)為理想脈沖響應(yīng)與窗函數(shù)乘積
　　　　[db,mag,pha,grd,ω]=freqz_m(h,^[1]);
　　　　delta_ω=2*π/1000;
　　　　Rp=-(min(db(ωp/delta_ω+1:1:501)));
　　　　disp([’實(shí)際通帶波動(dòng)為’,num2str(Rp)]);　　　%以下為作圖程序
　　　　As=-round(max(db(1:1:ωs/delta_ω+1)));
　　　　disp([’最小阻帶衰減為’,num2str(As)]);
　　　　　　subplot(1,1,1);
　　　　　　subplot(2,2,1);
　　　　　　stem(n,hd);
　　　　　　title(’理想脈沖響應(yīng)’);　
　　　　　　axis([0 M-1 -0.4 0.8]);
　　　　　　ylabel(’hd(n)’);
　　　　　　subplot(2,2,2);
　　　　　　stem(n,w_kai);
　　　　　　title(’凱澤窗’);
　　　　　　 axis([0 M-1 0 1.1]);
　　　　　　ylabel(’wd(n)’);
　　　　　　subplot(2,2,3);
　　　　　　stem(n,h);
　　　　　　title(’實(shí)際脈沖響應(yīng)’);
　　　　　　axis([0 M-1 -0.4 0.8]);
　　　　　　xlabel(’n’);ylabel(’h(n)’);
　　　　　　subplot(2,2,4);
　　　　　　plot(ω/π,db);
　　　　　　title(’幅度響應(yīng)/dB’);
　　　　　　axis([0 1 -100 10]);
　　　　　　grid;
　　　　　　xlabel(’以π為單位的頻率’);
　　　　　　ylabel(’分貝數(shù)/dB’);
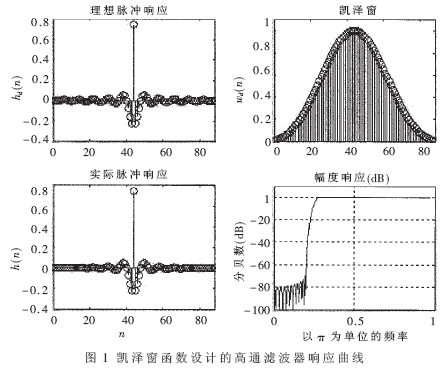
　　程序運(yùn)行結(jié)果如圖1所示。實(shí)際通帶波動(dòng)為0.04369,最小阻帶衰減為70,，濾波器長度為89,，線性相位斜率為6.7553,符合設(shè)計(jì)要求。

2．2 低通濾波器的設(shè)計(jì)
　　用窗函數(shù)設(shè)計(jì)低通濾波器,，性能指標(biāo)如下：通帶截止頻率ω_p=0.1π,，阻帶截止頻率ω_s=0.25π，實(shí)際通帶波動(dòng)R_p=0.10dB,最小阻帶衰減A_s=40dB。
　　分析：從表1可以看出,，漢寧窗,、海明窗和凱澤窗能提供大于40dB的最小阻帶衰減。但漢寧窗的旁瓣峰值較小,，而主瓣寬度和海明窗一樣,。可以使濾波器的階數(shù)較少,，所以選用漢寧窗進(jìn)行設(shè)計(jì),，程序主要部分如下：
　　ωp=0.10*π;
　　ωs=0.25*π;　
　　tr_width=ωs-ωp; %計(jì)算過渡帶寬
　　M=ceil(6.6*/tr_width)+1; %按漢寧窗計(jì)算濾波器長度
　　disp([’濾波器的長度為’,num2str(M)]);
　　n=0:M-1;
　　ωc=(ωs+ωp)/2; %截止頻率取為兩邊緣頻率的平均值
　　hd=ideal_lp(ωc,M); %求理想脈沖響應(yīng)
　　w_han=(hanning(M))’; %求漢寧窗函數(shù)
　　h=hd.*w_han; %設(shè)計(jì)的脈沖響應(yīng)為理想脈沖響應(yīng)與窗函數(shù)乘積
　　[db,mag,pha,grd,ω]=freqz_m(h,^[1]);%以下為作圖語句
　　delta_ω=2*π/1000;
　　Rp=-(min(db(1:1: ωp/delta_ω+1)));
　　disp([’實(shí)際通帶波動(dòng)為’,num2str(Rp)]); %以下為作圖程序
　　As=-round(max(db(ωs/delta_ω+1:1:501)));
　　disp([’最小阻帶衰減為’,num2str(As)]);
　　　　subplot(221)
　　　　stem(n,hd);
　　　　title(’理想沖擊響應(yīng)’),
　　　　axis([0 M-1 -0.1 0.3]);
　　　　ylabel(’hd(n)’);
　　　　subplot(222)
　　　　stem(n,w_han);
　　　　title(’漢寧窗’),
　　　　axis([0 M-1 0 1.1]);
　　　　ylabel(’wd(n)’);
　　　　subplot(223)
　　　　stem(n,h);
　　　　title(’實(shí)際沖擊響應(yīng)’),
　　　　axis([0 M-1 -0.1 0.3]);
　　　　xlabel(’n’);
　　　　ylabel(′h(n)′);
　　　　subplot(224);
　　　　plot(ω/π,db);
　　　　title(′幅度響應(yīng)（db)′);
　　　　axis([0 1 -100 10]),
　　　　grid;
　　　　xlabel(′以π為單位的頻率′);
　　　　ylabel(′分貝數(shù)′);
　　　　仿真結(jié)果如圖2所示。實(shí)際通帶波動(dòng)為0.076565,最小阻帶衰減為44,，濾波器長度為67,，符合設(shè)計(jì)要求。