隨著空間遙感技術(shù)的發(fā)展,，超光譜成像技術(shù)在資源勘測、環(huán)境調(diào)查,、災(zāi)害預(yù)報,、軍事偵察等領(lǐng)域得到越來越廣泛的應(yīng)用。并且,，隨著光譜層析技術(shù)與電子技術(shù)的不斷成熟,，成像光譜儀的空間分辨率越來越高，波段數(shù)越來越多,，產(chǎn)生的數(shù)據(jù)量也越來越大,，給存儲和傳輸帶來了很多困難。因此,，必須對超光譜遙感圖像進行有效的壓縮,，以滿足衛(wèi)星遙感平臺的應(yīng)用需要。
　　從其成像原理看,，超光譜圖像像素之間存在兩種相關(guān)性：同一波段內(nèi)像素之間的空間相關(guān)性和不同波段像素之間的譜間相關(guān)性,。同時，與自然圖像相比,，超光譜圖像含有豐富的紋理信息，空間相關(guān)性較差,，而譜間相關(guān)性很強,。在對超光譜圖像進行壓縮時，要有效地去除這兩種相關(guān)性,。
　　近年來,，小波變換方法在圖像壓縮領(lǐng)域得到了廣泛的應(yīng)用。小波變換具有空間——頻率域內(nèi)的局部化特性,，能對圖像進行多分辨率分解,，較好地去除像素間的相關(guān)性，同時保持圖像在各個分辨率下的精細結(jié)構(gòu),，有利于圖像的壓縮編碼,。目前，出現(xiàn)了很多基于小波變換的圖像壓縮算法,，比較有代表性的有Shapiro^[1]提出的EZW算法,、Said和Pearlman^[2]提出的SPIHT算法、Islam等提出的SPECK算法以及Taubman^[4]提出的被采納為JPEG2000標(biāo)準(zhǔn)核心壓縮算法的EBCOT算法,。很多學(xué)者將這些算法應(yīng)用到超光譜圖像壓縮中,，并針對超光譜圖像的特點，研究了適合超光譜圖像壓縮的方法,，例如Dragotti等^[5]使用K L變換去除光譜維的譜間相關(guān)性,，使用2D DWT去除空間相關(guān)性,，隨后用一種3維SPIHT算法對變換系數(shù)進行量化編碼。另外,，WANG Qi等^[6]使用1+2維小波變換去除超光譜圖像的空間相關(guān)性和譜間相關(guān)性,，對每一波段圖像的小波系數(shù)采用EBCOT方法進行壓縮編碼。
　　本文在這些研究成果的基礎(chǔ)上,，提出一種基于小波變換的3維SPECK編碼算法,。該算法首先對超光譜圖像序列進行3維小波變換，同時去除空間相關(guān)性和譜間相關(guān)性,，然后將SPECK算法擴展到3維,，構(gòu)造一種3維SPECK算法對小波系數(shù)進行壓縮編碼。實驗證明,，3D SPECK算法具有良好的率失真性能,，其壓縮效果遠遠優(yōu)于采用SPECK方法對每一波段圖像小波系數(shù)做壓縮編碼的效果。同時,，與3維SPIHT算法^[5]相比較,，此算法具有更低的運算復(fù)雜度，并具有嵌入式的特性,，能夠滿足不同壓縮應(yīng)用,。
1 SPECK編碼算法
　　圖像經(jīng)過小波變換后，低頻子帶上集中了大部分的重要性小波系數(shù),，而各個高頻子帶上分散著大部分的不重要小波系數(shù),。在漸進傳輸?shù)那度胧綀D像壓縮系統(tǒng)中，重要性系數(shù)要優(yōu)先進行編碼傳輸,，以便解碼時首先得到圖像的概貌部分,，然后對不重要系數(shù)進行編碼傳輸，進而得到圖像的細節(jié)部分,。在EZW和SPIHT算法中,，主要利用零樹結(jié)構(gòu)來對這些不重要系數(shù)進行編碼，雖然利用了子帶之間不重要系數(shù)的相關(guān)性,，但沒有充分利用同一子帶中不重要系數(shù)的相關(guān)性,，而SPECK算法將子帶中的小波系數(shù)組織成矩形的塊，對系數(shù)塊進行分割排序,，充分利用了同一子帶中系數(shù)的相關(guān)性,。
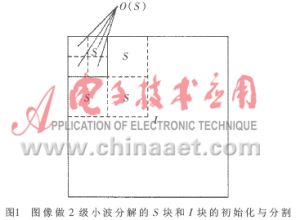
　　SPECK算法中，程序處理的基本單元是系數(shù)塊,，塊分為兩種類型： S類型的塊和I類型的塊,。算法初始時，將圖像的所有小波系數(shù)分割為一個 S塊和一個I塊， S塊包含最低頻子帶的系數(shù),，I塊包含除去 S塊中系數(shù)以后剩余的系數(shù),。定義一個判決塊重要與否的符號函數(shù)S_n為：
　　
　　若S_n(S)=1或S_n(I)=1，則認為S塊或I塊是重要的,，并對重要的S塊或I塊進行分割,，分割為更小的子塊" title="子塊">子塊，S塊和I塊的分割如圖1所示,。

　　算法中,，還用到兩個存儲系數(shù)塊的列表：LIS和LSP。LIS為不重要集合表,，存放當(dāng)前閾值下不重要的系數(shù)塊,，以便在下一閾值對這些塊進行處理，LIS初始化為初始S塊中的系數(shù),；LSP是重要系數(shù)表,，存放重要的且只包含一個系數(shù)的系數(shù)塊，以便對這些系數(shù)做精細量化,，LSP初始化為空表,。
　　編碼過程中，算法在不同的閾值下對S塊和I塊分別進行處理,，確定重要性小波系數(shù),，對重要的小波系數(shù)優(yōu)先進行量化編碼。針對S塊和I塊,，算法的處理過程分別為：對S塊,，如果S塊是不重要的，將S塊放入LIS中,；如果S塊是重要的，采用四叉樹分割方法,，將S塊分割為4個大小相等(或近似相等)的子塊,，對每一子塊重復(fù)相同的過程，直到找到重要性系數(shù),，將重要性系數(shù)放入LSP中以待精細量化,。對I塊，如果I塊是不重要的,，將I塊保留,，在下一閾值對I塊做重新處理；如果I塊是重要的,，按照分割策略,，將I塊分割為3個S塊和1個較小的I塊，并對分割得到的S塊和I塊分別做相應(yīng)的處理。
2 超光譜圖像的3維SPECK編碼
　　超光譜圖像是利用光譜儀對同一地物目標(biāo)在多個離散光譜波段上成像的結(jié)果,，因此在2維空間信息的基礎(chǔ)上增加了1維光譜信息,，而像素之間的相關(guān)性除了同一波段內(nèi)的空間相關(guān)性以外，還增加了不同波段之間的譜間相關(guān)性,。在對超光譜圖像做小波變換時,，應(yīng)在空間維和光譜維分別做小波變換，即采用3維小波變換,，同時去除像素數(shù)據(jù)間的空間相關(guān)性和譜間相關(guān)性,。
　　為了分析和計算的方便，小波變換通常采用可分離的方式,。本文在對超光譜圖像做3維小波變換時,，采用可分離的金字塔分解方式，在圖像的行,、列,、光譜方向分別做1維小波變換，并且只對低頻子帶做小波分解,，使圖像能量集中在最低頻子帶的小波系數(shù)上,。在對圖像做小波變換時，小波基的選取會對變換后的壓縮產(chǎn)生很大的影響,。好的小波基能最大限度地去除圖像的相關(guān)性,，同時能較好地保持圖像的紋理、避免較大的邊界失真,，利于圖像的編碼和重構(gòu),。文獻^[7]證明，由B樣條小波基構(gòu)成的9/7雙正交小波具有良好的正則性和緊支性,，并具有線性相位的特點,，濾波器長度適中，變換后對圖像的影響不大,，最利于壓縮應(yīng)用,。因此，本文在對超光譜圖像做3維小波變換時,，即采用9/7雙正交小波濾波器,。
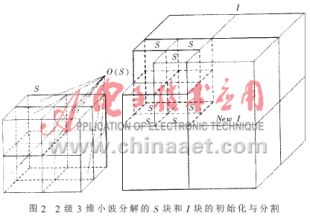
　　超光譜圖像經(jīng)過3維小波變換后，重要性小波系數(shù)大部分集中到最低頻子帶的3維系數(shù)塊中,，而不重要系數(shù)分散到各個高頻子帶的3維系數(shù)塊中,。在用SPECK算法對系數(shù)進行編碼時，程序處理的系數(shù)塊將是3維的,。相應(yīng)地,，算法也將擴展到3維,，構(gòu)造出一種3維SPECK算法，對這些系數(shù)塊進行分割排序,。在3維SPECK算法中,，小波系數(shù)用坐標(biāo)(x,y,z)標(biāo)識，x表示系數(shù)在水平方向的位置,，y表示系數(shù)在垂直方向的位置,，z表示系數(shù)在光譜方向的位置，系數(shù)的值用C(x,y,z)表示,。系數(shù)塊分為兩種類型：S類型塊和I類型塊,。初始時，將所有小波系數(shù)分割為一個3維的S塊和一個3維的I塊,。S塊包含最低頻子帶的系數(shù),，例如經(jīng)過2級小波分解后對應(yīng)于LLL2子帶中的系數(shù)。I塊則包含除去S塊系數(shù)以后剩余的系數(shù),，例如經(jīng)過2級小波分解后對應(yīng)于HLL2,、LHL2、HHL2,、LLH2,、HLH2、LHH2,、HHH2,、HLL1、LHL1,、HHL1,、LLH1、
　　HLH1,、LHH1,、HHH1子帶中的系數(shù)。算法對3維S塊和3維I塊的分割處理如圖2所示,。

　　對3維S塊的處理過程：對重要的S塊,，將其分割為8個大小相等(或近似相等)的子塊，對每一個子塊,，測試其重要性，對重要的子塊進行再次分割,，直至定位到重要性系數(shù),，將重要性系數(shù)放入LSP中；對不重要的S塊,，放入LIS中,，在下一閾值重新處理,。在分割過程中，如果S塊的第3維即光譜維的大小為1時,，則S塊只在空間維進行分割,，分割為4個大小相等的子塊。對3維I塊的處理過程：對重要的I塊,，將其分割為7個S塊(如圖2示)和一個較小的I塊,，每個S塊包含相應(yīng)尺度下一個子帶的系數(shù)，對分割后得到的S塊和I塊分別做相應(yīng)的分割處理,；對不重要的I塊,，將其保留，不做分割,，在下一閾值重新處理,。算法詳細描述如下：
　　第一步：初始化
　　·將小波系數(shù)分割為S塊和I塊，S={(x,y,z)|(x,y,z)∈Root},，Root為最低頻子帶系數(shù)集合,，I塊包含除去S塊中系數(shù)后的剩余系數(shù)；
　　·閾值：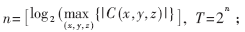
　　·不重要集合表：LIS={S},；重要性系數(shù)表：LSP={},；
　　第二步：分割排序過程
　　·按塊從小到大的順序，對每一個S∈LIS,，執(zhí)行processS(S),，對S塊進行分割；
　　·執(zhí)行processI(),，對I塊進行分割,；
　　processS(S)
　　{
　　輸出S_n(S)；
　　if S_n(S)=1
　　——if S是單個系數(shù),，輸出S的符號并將S放入LSP中,；
　　——else執(zhí)行codeS(S)；
　　——if S∈LIS,，將S從LIS中刪除,；
　　else
　　——if S∈LIS，將S放入LIS中,；
　　}
　　codeS(S)
　　{
　　將S分割為8個大小相等(或近似相等)的子塊O(S),，如果S塊的第3維即光譜維的大小為1，則S塊只在空間維進行分割,，分割為4個大小相等的子塊,；
　　對每一個子塊O(S)
　　——輸出S_n(O(S))；
　　——if S_n(O(S))=1
　　——if O(S)是單個系數(shù),，輸出O(S)的符號并將O(S)放入LSP中,；
　　——else執(zhí)行codeS(O(S)),；
　　——else
　　——將O(S)放入LIS中；
　　}
　　processI()
　　{
　　　輸出S_n(I),；
　　　if S_n(I)=1
　　　——執(zhí)行codeI(),；
　　}
　　codeI()
　　{
　　　將I分割為7個S塊和1個較小的I塊(如圖2示)；
　　　對每一個S塊,，執(zhí)行processS(S),；
　　　對I塊，執(zhí)行processI(),；
　　}
　　第三步：精細量化過程
　　·對每一個(x,y,z)∈LSP,，除了最后一次排序過程放入的系數(shù)外，輸出|C(x,y,z)|的第n個最重要位,；
　　第四步：閾值更新
　　·n=n-1,；轉(zhuǎn)移到第二步；
3 仿真實驗結(jié)果
　　本文采用224波段AVIRIS超光譜成像儀拍攝的山地圖像來驗證提出的基于3維SPECK編碼的超光譜圖像壓縮算法,。每一波段圖像為256×256的灰度圖,，每個像素數(shù)據(jù)8bit，選擇172～187波段作為驗證算法的實驗數(shù)據(jù),。
　　對此16個波段的圖像序列,，采用由B樣條小波基構(gòu)成的9/7雙正交小波濾波器，做4級3維小波變換,，將圖像序列分解為29個子帶的小波系數(shù),。對這些子帶的小波系數(shù)塊，用本文提出的3維SPECK算法進行壓縮編碼,。
　　為了客觀評價圖像壓縮的質(zhì)量,，本文采用兩個失真評價準(zhǔn)則：平均均方誤差MSE和平均峰值信噪比PSNR，定義為：
　　
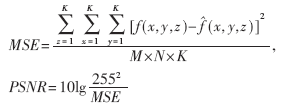
　　式中,，f(x,y,z)為原始圖像序列的灰度函數(shù),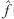，(x,y,z)為解碼圖像的灰度函數(shù)。
　　為了與零樹編碼方法做壓縮性能比較,，本文除了采用3維SPECK算法對小波系數(shù)編碼外,，還采用3維SPIHT算法對小波系數(shù)做壓縮編碼。同時,，還使用2維SPECK編碼算法對每一波段圖像的小波系數(shù)做壓縮編碼,，與3維SPECK算法的壓縮結(jié)果做比較。壓縮結(jié)果如表1所示,。

　　從實驗結(jié)果可以看出：對整體圖像序列采用3維SPECK方法的壓縮效果要遠遠優(yōu)于對每一波段圖像采用2維SPECK方法的壓縮效果,。這主要是因為超光譜圖(接上頁)
　　像的空間相關(guān)性較差，圖像的紋理細節(jié)非常豐富,，而不同波段圖像的紋理和邊緣非常近似,，圖像之間存在紋理結(jié)構(gòu)上的相關(guān)性，3維SPECK方法很好地利用了這種結(jié)構(gòu)相關(guān)性,，因此取得了較2維SPECK方法更好的壓縮性能,。
　　另外，為了與基于小波零樹的編碼方法做性能比較,，本文采用了3維SPIHT方法對小波系數(shù)進行編碼,。從實驗結(jié)果可以看出，在相同碼率下,，此算法的峰值信噪比較3維SPIHT方法有很微小的降低,。然而，SPECK方法處理的是小波系數(shù)塊,，不需要像SPIHT方法那樣在整個小波系數(shù)域內(nèi)搜索零樹,，因此，計算復(fù)雜性和資源需求比SPIHT方法低,。這一點對衛(wèi)星遙感平臺的應(yīng)用很重要,。
參考文獻
1 J.M.Shapiro. Embedded image coding using zerotrees of wavelets coefficients[J].IEEE Trans.Signal Processing，1993,；41(12)：3450～3462
2 A.Said,，W.A.Pearlman. A new fast and efficient image codec based on set partitioning in hierarchical trees[J].IEEE Trans.Circuits and Systems for Video Technology，1996,；6(6)：243～250
3 A.Islam,，W.A.Pearlman.An embedded and efficient low-complexity hierarchical image coder[C].San Jose：SPIE Opt Soc,1999：294～305
4 D.Taubman.High performance scalable image compression with EBCOT[J].IEEE Trans.Image Processing，2000,；9(7)：1158～1170
5 P.L.Dragotti,，G. Poggi，A.R.P.Ragozini.Compression of mult-ispectral images by three-dimensional SPIHT algorithm[J].IEEE Trans.Geoscience and Remote Sensing,，2000,；38(1)：416～427
6 王 琪，郭 雷. 基于1+2維小波變換的多光譜圖像壓縮[J].光子學(xué)報,，2003,；32(9)：1126～1129
7 ANTONINI M，BARLAUD M,，MATHIEU P .Image coding using wavelet transform[J].IEEE Trans.Image Processing,，1992；1(2)：205～220