0引言
結(jié)冰傳感器是用于探測結(jié)冰厚度的設(shè)備,。它是基于振動原理設(shè)計(jì)的，振動體采用振管形式,。當(dāng)振管垂直立于環(huán)境中時(shí),，激振電路為振管提供交變磁場,，振管在磁場的作用下產(chǎn)生磁致伸縮作軸向振動，同時(shí)信號拾取電路將此機(jī)械振動信號轉(zhuǎn)變?yōu)殡娦盘柗答伣o激振電路,，使電路諧振于振管的軸向振動固有頻率上,。根據(jù)振動理論，當(dāng)振管表面出現(xiàn)冰層時(shí),，其軸向振動固有頻率會產(chǎn)生偏移,，使電路的諧振頻率也產(chǎn)生偏移，因此根據(jù)頻率偏移量即可確定冰層的厚度,。
d=F(f′-f0)　　　　(1)
式中：d為冰層厚度,；
f′為結(jié)冰后的振動頻率；
f0為結(jié)冰前的振動頻率,。
f0為定值,，所以冰層厚度只與頻率值f′有關(guān)系，但頻率值與冰層厚度為非線性關(guān)系,，不能簡單地由頻率值確定所測的冰層厚度,，這樣增加了厚度顯示和處理的復(fù)雜性。為了保證一定的測量精度以便于在測控系統(tǒng)中應(yīng)用,，必須對其進(jìn)行非線性校正,。
以前一直采用表格法進(jìn)行數(shù)據(jù)處理，通過分段線性化法來逼近傳感器的靜態(tài)特性曲線，簡單,、實(shí)用,。但當(dāng)表格小時(shí)，精度受到影響,；表格大時(shí),，實(shí)時(shí)性受影響，對傳感器的處理器提出了嚴(yán)格的要求,。
神經(jīng)網(wǎng)絡(luò)方法為傳感器的非線性校正方法的研究開辟了新的途徑,。具體做法是，以實(shí)驗(yàn)數(shù)據(jù) 為樣本訓(xùn)練BP網(wǎng)絡(luò),，得到結(jié)冰傳感器的逆模型,，從而使傳感器經(jīng)神經(jīng)網(wǎng)絡(luò)組成的系統(tǒng)線性化，傳感器的非線性特性得到補(bǔ)償,，校正后的網(wǎng)絡(luò)可按線性特性處理,，提高了測量精度，大大拓展了結(jié)冰傳感器的應(yīng)用范圍,。

1BP網(wǎng)絡(luò)
人工神經(jīng)網(wǎng)絡(luò)是一門新興交叉學(xué)科,。在人工神經(jīng)網(wǎng)絡(luò)的實(shí)際應(yīng)用中，80%～90 %的人工神經(jīng)網(wǎng)絡(luò)模型是采用BP神經(jīng)網(wǎng)絡(luò),。它是一種前饋神經(jīng)網(wǎng)絡(luò),，通常由輸入層、輸出層和若干隱含層組成,，相鄰層之間通過突觸權(quán)矩陣連接起來,。研究最多的是一個隱含層的網(wǎng)絡(luò)，因?yàn)?層的前饋網(wǎng)絡(luò)就能逼近任意的連續(xù)函數(shù),。
各層節(jié)點(diǎn)的輸出按下式計(jì)算

式中yi是節(jié)點(diǎn)輸出,，xi是節(jié)點(diǎn)接收的信息，wij是相關(guān)連接權(quán)重,，θi為閾值,，n是節(jié)點(diǎn)數(shù)。

2用BP網(wǎng)絡(luò)進(jìn)行數(shù)據(jù)擬合
2.1基本原理
采用神經(jīng)網(wǎng)絡(luò)方法對傳感器輸出特性進(jìn)行數(shù)據(jù)擬合的原理圖由傳感器模型和神經(jīng)網(wǎng) 絡(luò)校正模型兩部分組成,，如圖1所示,。圖中，假設(shè)傳感器的靜態(tài)輸入輸出的特性為y=f(x),。采用實(shí)驗(yàn)值通過對BP網(wǎng)進(jìn)行訓(xùn)練,，可以得到傳感器的逆模型x=f－1(y)。對于任意輸出yi,，都可以找到輸入輸出特性曲線上對應(yīng)的輸入xi,，從而實(shí)現(xiàn)了線性化,。



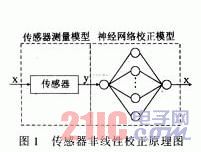
2.2學(xué)習(xí)算法
BP網(wǎng)絡(luò)的基本學(xué)習(xí)算法是誤差反向傳播學(xué)習(xí)算法。這種算法簡單,、實(shí)用,，但從數(shù)學(xué)上看它歸結(jié)為一非線性的梯度優(yōu)化問題，因此不可避免的存在局部極小問題,，學(xué)習(xí)算法的收斂速度慢，通常需要上千次或更多,。
近些年許多專家對學(xué)習(xí)算法進(jìn)行了廣泛的研究,，現(xiàn)在已發(fā)展了許多的改進(jìn)學(xué)習(xí)算法，如快速下降法,、Levenberg-Marquardt法等,，收斂速度快，能滿足實(shí)時(shí)性要求,。
其中Levenberg-Marquardt法簡稱L-M算法,，是一種將最陡下降法和牛頓法相結(jié)合的算法。它的本質(zhì)是二階梯度法,，故具有很快的收斂速度,。基于此,，文中采用L-M算法來訓(xùn)練BP網(wǎng)絡(luò),。它不需要計(jì)算Hessian矩陣，而是利用式(3)進(jìn)行估算：

式中,，J為Jacobian矩陣,，包括網(wǎng)絡(luò)誤差項(xiàng)相對于權(quán)重和閾值的一階微分 ，e為網(wǎng)絡(luò)的誤差項(xiàng),。Jacobian矩陣可以利用標(biāo)準(zhǔn)的BP算法得出,，這比直 接計(jì)算Hessian矩陣簡單得多。LM算法的迭代式為：
　　　
如果比例系數(shù)μ=0,，則為牛頓法,，如果μ取值很大，則接近梯度下降法,，每迭代成 功一步,，則μ減小一些，這樣在接近誤差目標(biāo)的時(shí)候,，逐漸與牛頓法相似,。牛頓法在接近誤 差的最小值的時(shí)候，計(jì)算速度更快,，精度也更高,。實(shí)踐證明,，采用該方法可以較原來的梯度 下降法提高速度幾十甚至上百倍。
2.3MATLAB中學(xué)習(xí)過程與仿真
MATLAB6.2中的神經(jīng)網(wǎng)絡(luò)工具箱功能強(qiáng)大,，不但能方便創(chuàng)建常見的神經(jīng)網(wǎng)絡(luò),，還支 持用戶自己構(gòu)造網(wǎng)絡(luò)。
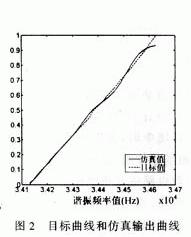
在實(shí)際中,，根據(jù)測量范圍和精度要求,，以實(shí)驗(yàn)中的101個數(shù)據(jù)為樣本，在MATLAB中構(gòu)造BP網(wǎng)絡(luò)進(jìn)行訓(xùn)練,。在訓(xùn)練之前,，對數(shù)據(jù)進(jìn)行了預(yù)處理。諧振頻率值為輸入樣本P,，將冰層厚度變換到［－1,，1］的范圍后作為輸出樣本t。訓(xùn)練完后,，再通過后處理還原回原來的樣本空間,。神經(jīng)網(wǎng)絡(luò)模型為單輸入單輸出，隱含層有5個神經(jīng)元,，訓(xùn)練中誤差指標(biāo)定為0.01,。訓(xùn)練結(jié)果如圖2、圖3,、表1,。訓(xùn)練進(jìn)行了15步就滿足了誤差要求，收斂速度較快,。

3結(jié)束語
神經(jīng)網(wǎng)絡(luò)作為一種分析,、處理問題的新方法已經(jīng)在很多領(lǐng)域顯示了強(qiáng) 大的生 命力。由于神經(jīng)網(wǎng)絡(luò)具有高速并行計(jì)算能力和非線性變換能力,，能夠隨時(shí)進(jìn)行再學(xué)習(xí)且學(xué)習(xí) 效率很高,， 特別對于產(chǎn)品性能一致性不高的結(jié)冰傳感器更見其效果。相對其他校正方式而言,，神經(jīng)網(wǎng)絡(luò) 無須深入了解對象的機(jī)理,，具 有很強(qiáng)的曲線擬合能力。實(shí)驗(yàn)表明,，補(bǔ)償?shù)男Ч钊藵M意,，大大方便了結(jié)冰傳感器在測控系 統(tǒng)中的應(yīng)用。