0 引言

    擴展卡爾曼濾波(Extended Kalman Filter,，EKF)是解決非線性系統(tǒng)狀態(tài)估計問題的最經(jīng)典濾波技術(shù)^[1-3],。然而，EKF濾波存在一些缺點,，例如系統(tǒng)動力學模型和測量模型需可微,；狀態(tài)估計對偏差比較敏感甚至會濾波發(fā)散^[4]。另外,，由于EKF的測量更新不能使濾波結(jié)果達到最大似然值,，研究者們提出了擴展卡爾曼濾波的迭代形式(Iterated Extended Kalman Filter，IEKF)^[5-7],。在狀態(tài)預測之后,，IEKF測量更新會進行迭代,，從而得到優(yōu)于EKF的估計結(jié)果，且在廣泛的應用中已經(jīng)得到驗證^[8-9],。為了減少狀態(tài)預測對最終估計的影響,，提出了修正迭代擴展卡爾曼濾波(Modified Iterated Extended Kalman Filter，MIEKF)算法^[10-11],，該方法在迭代過程中使用測量更新的狀態(tài)估計代替狀態(tài)預測,，然后利用與IEKF中相同的高斯-牛頓方法求解。然而,，進一步研究發(fā)現(xiàn),，在第一次迭代之后，測量噪聲信息已被包含到估計的狀態(tài)中,，因此系統(tǒng)狀態(tài)和估計的狀態(tài)將不與測量噪聲之間保持相互獨立,。綜上，為了應用于更高精度的估計場合中,，有必要研究新的濾波技術(shù)來解決上述問題,。

    受CHANG L B等人^[12-13]和文獻[14]中思想的啟發(fā)，本文提出一種基于狀態(tài)增廣的修正迭代擴展卡爾曼濾波(State augmentation-based Modified Iterated Extended Kalman Filtering,，SMIEKF)算法,，即在迭代時將測量噪聲直接增廣到系統(tǒng)狀態(tài)中，與經(jīng)典的EKF和MIEKF相比,，該濾波算法在收斂速度和估計精度方面均更優(yōu),。

1 非線性濾波問題

    一般的非線性離散時間濾波問題可描述為：

其中，x_k代表狀態(tài)向量,；w_k代表t_k時刻的隨機輸入,，且w_k的均值為0，協(xié)方差為Q_k,。

    測量模型可表示為：

其中,，y_k代表t_k時刻的測量值；v_k代表t_k時刻的測量噪聲,，且v_k的均值為0,，協(xié)方差為R_k。

2 基于狀態(tài)增廣的修正迭代擴展卡爾曼濾波

2.1 修正迭代擴展卡爾曼濾波

    在非線性測量情況下,，當局部線性化能無條件滿足時,，與EKF相比，IEKF具有優(yōu)越的性能,。但是,，當初始估計誤差較大時，IEKF的性能將會降低甚至低于EKF的濾波精度,。另外,，在IEKF的測量更新迭代過程,，直接將EKF的狀態(tài)預測作為迭代步驟的初始值，而該值對最終估計的狀態(tài)具有直接且巨大的影響,。當系統(tǒng)狀態(tài)能完全被測量數(shù)據(jù)觀測時,，最終狀態(tài)估計比狀態(tài)預測值更接近真實值^[15]。如果將最終狀態(tài)估計用于非線性迭代更新的初始值并利用高斯-牛頓方法解決該問題,，則該算法稱為修正迭代擴展卡爾曼濾波(MIEKF),，且MIEKF修正的測量更新等式為^[10-11]：

    顯然，當進行一步迭代后測量噪聲信息被包含到估計的狀態(tài)中,，從而導致系統(tǒng)狀態(tài)和測量噪聲之間不再滿足正交性,，式(3)便不再成立，因此,，仍然采用式(3)使得濾波算法的精度大大降低,。基于此,，本文提出了基于狀態(tài)增廣的修正迭代擴展卡爾曼濾波來解決此問題。

2.2 基于狀態(tài)增廣的修正迭代擴展卡爾曼濾波算法

    本文提出基于狀態(tài)增廣的修正迭代擴展卡爾曼濾波(SMIEKF)的狀態(tài)估計算法,，SMIEKF算法的偽碼運行過程如下：

    由于測量噪聲已被包含到系統(tǒng)狀態(tài)中,，使得新測量噪聲相對于增廣的系統(tǒng)狀態(tài)為零，而零向量與所有向量均正交,。因此,，保證了狀態(tài)和測量噪聲之間的正交性。

3 算法仿真

    在本節(jié)中,，通過使用從雷達地面站記錄的距離測量數(shù)據(jù)再現(xiàn)彈道目標的軌跡來驗證所提SMIEKF濾波方法的性能,，目的是估計彈道目標在重新進入具有恒定但未知的阻力系數(shù)大氣層時的軌跡。在系統(tǒng)動態(tài)模型中不考慮作用在目標上的重力加速度,，原因在于這種改進的模型對于高初始速度是有效的,，這使得空氣動力加速度較重力加速度占主導地位。另外,，從雷達跟蹤站記錄距離測量數(shù)據(jù),。由于其在動態(tài)和測量模型中具有顯著的非線性，因此該示例在濾波算法研究工作中被廣泛引用,。

3.1 動力學與測量模型

    上述問題的動力學模型為：

其中v_k指具有零均值的測量噪聲向量,，且它的概率密度函數(shù)為p(v_k)；a是雷達的高度,；b是雷達和彈道目標間的水平距離,。測距信息從頻率為1 Hz的雷達跟蹤站獲得。仿真參數(shù)和初始條件見表1和表2^[16],。

3.2 仿真結(jié)果分析

    在該仿真中,，使用四階龍格-庫塔方法對連續(xù)時間動態(tài)方程離散化,，且將時間步長設置為1 s。兩種迭代濾波算法均執(zhí)行三次迭代,，共進行100次蒙特卡羅模擬仿真,，每次運行過程都使用不同的噪聲樣本，以便計算出濾波誤差的中值估計的絕對值,，從而對三種濾波算法的性能進行公平地比較,。蒙特卡羅仿真的結(jié)果如圖1~圖3所示。

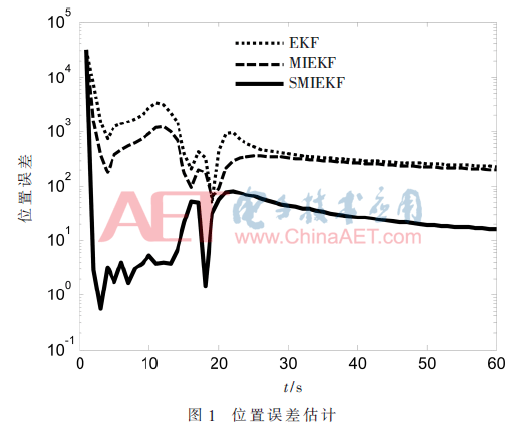
    仿真結(jié)果表明,，與標準的EKF和MIEKF相比,，SMIEKF具有最好的性能；且MIEKF比標準EKF性能更優(yōu),。原因在于：在MIEKF測量更新過程中,，系統(tǒng)狀態(tài)與測量噪聲相互獨立，但在執(zhí)行第一次迭代后,，這將不再成立,。相比之下，在所提出的SMIEKF算法中,，將測量噪聲增廣到狀態(tài)變量中,，則對應于增廣后狀態(tài)的新測量噪聲為零，且零向量在統(tǒng)計學上與任何向量均正交,，使得增廣后的狀態(tài)與測量噪聲仍保持相互獨立,，因此SMIEKF可得到比MIEKF更精確的預測測量誤差協(xié)方差，從而在三種濾波算法中呈現(xiàn)出最優(yōu)的狀態(tài)估計性能,。

4 結(jié)論

    本文基于狀態(tài)增廣方法提出了一種性能增強的SMIEKF濾波算法,，該方法主要是在測量更新的迭代過程中，將測量噪聲增廣到系統(tǒng)狀態(tài)中,，使得新的系統(tǒng)狀態(tài)獨立于迭代過程中相應的測量噪聲,，從而得到更好的濾波結(jié)果。仿真結(jié)果也表明,，與MIEKF和傳統(tǒng)的EKF相比,，所提出的濾波方法具有更優(yōu)的性能。

參考文獻

[1] LERRO D,，BAR-SHALOM Y.Tracking with debiased consistent converted measurements versus EKF[J].IEEE Transactions on Aerospace and Electronic Systems,，1993，29(3)：1015-1022.

[2] 黃樹清,，胡方強,，包亞萍，等.抑制多徑的BD2/GPS雙模自適應擴展卡爾曼濾波算法[J].電子技術(shù)應用，2017,，43(2)：77-80.

[3] 李敏濤.基于RAEKF的GPS/INS緊組合導航方法研究[J].電子技術(shù)應用,，2019，45(2)：33-36.

[4] ATHANS M,，WISHER R P,，BERTOLINI A.Suboptimal state estimation for continuous-time nonlinear systems from discrete noise measurements[J].IEEE Transactions on Automatic Control，1968,，13(5)：504-515.

[5] BELL,，B M，CATHEY F W.The iterated Kalman filter update as a Gauss-Newton method[J].IEEE Transactions on Automatic Control,，1993,，38(2)：294-297

[6] GELB A.Applied optimal estimation[D].The Massachusetts Institute of Technology Press：Cambridge，MA,，USA,，1974.

[7] BAR-SHALOM Y，LI X R,，KIRUBARAJAN T.Estimation with application to tracking and navigation：theory,，algorithm，and software[M].New York：Wiley,，2001.

[8] KARLGAARD C D.Nonlinear regression Huber-Kalman filtering and fixed-interval smoothing[J].Journal of Guidance,，Control and Dynamics，2015,，38(2)：322-330.

[9] LI W，LIU M H,，DUAN D.Improved robust Huber-based divided difference filtering[J].Proceedings of the Institution of Mechanic Engineering,，Part G：Journal of Aerospace Engineering，2014,，228(11)：2123-2129.

[10] YANG Z,，ZHONG D，GUO F,，et al.Gauss-Newton iteration based algorithm for passive location by a single observer[J].Journal of Systems Engineering and Electronics,，2007，29(12)：2006-2009.

[11] ZHANG J,，JI H.Modified iterated extended Kalman filter based multi-observer fusion tracking for IRST[J].Journal of Systems Engineering and Electronics,，2010，32(3)：504-507.

[12] CHANG L B,，HU B Q,，CHANG G B.Multiple outliers suppression derivative-free filter based on unscented transformation[J].Journal of Guidance，Control and Dynamics，2012,，35：1902-1906.

[13] CHANG L B,，HU B Q，CHANG G B.Marginalised iterated unscented Kalman filter[J].IET Control Theory and Applications,，2012,，6(6)：847-854.

[14] LIU M，ZHAN X,，LI W.State augmentation-based iterated divided difference filtering[J].Proceedings of the Institution of Mechanic Engineering,，Part G：Journal of Aerospace Engineering，2015,，229(13)：2537-2544.

[15] LEFEBVRE T.,，BRUYNINCKX H，SCHUTTER DE J.Kalman filters for non-linear systems：a comparison of performance[J].International Journal of Control,，2004,，77：639-653.

[16] KARLGAARD C D，SCHAUB H.Comparison of several nonlinear filters for a benchmark tracking problem[C].AIAA Paper,，2006：2006-6243.

作者信息:

劉美紅1,，高山鳳1，李  偉2, 謝  彬3

(1.山西大學 自動化系,，山西 太原030006,；2.太原理工大學 自動化系，山西 太原030024,；

3.三菱重工海爾(青島)空調(diào)機有限公司,，山東 青島266200)