摘要：頻移鍵控(FSK)是用不同頻率的載波來傳遞數(shù)字信號,，并用數(shù)字基帶信號控制載波信號的頻率。提出一種基于流水線CORDIC算法的2FSK調(diào)制器的FPGA實現(xiàn)方案,，可有效地節(jié)省FPGA的硬件資源,，提高運算速度。最后,，給出該方案的硬件測試結(jié)果,，驗證了設(shè)計的正確性。

0 引言

頻移鍵控(FSK)是用不同頻率的載波來傳送數(shù)字信號,，并用數(shù)字基帶信號控制載波信號的頻率,。具有抗噪聲性能好、傳輸距離遠,、誤碼率低等優(yōu)點,。在中低速數(shù)據(jù)傳輸中，特別是在衰落信道中傳輸數(shù)據(jù)時,，有著廣泛的應(yīng)用,。傳統(tǒng)上以硬件實現(xiàn)載波的方法都是采用直接頻率合成器(DDS)實現(xiàn)。但是DDS傳統(tǒng)的實現(xiàn)方式是基于查找表思想,，即通過查找預(yù)先存儲的正余弦表來產(chǎn)生需要的正余弦值,。當(dāng)頻率、精度要求越高,，需要存儲的值也就越多,，考慮FPGA的RAM資源有限，傳統(tǒng)的DDS實現(xiàn)方式就有了應(yīng)用瓶頸,。因此導(dǎo)致開發(fā)成本過高,，甚至無法實現(xiàn)，不適合現(xiàn)代通信系統(tǒng)的發(fā)展,。

本文提出了應(yīng)用CORDIC(Coordinate Rotation Digital Computer)算法實時計算正弦值的方案,，并基于CORDIC算法在FPGA芯片上設(shè)計了2FSK調(diào)制器。這不僅能夠節(jié)省大量的FPGA邏輯資源,，而且能很好地兼顧速度,、精度,、簡單、高效等方面,。

1 CORDIC算法原理及結(jié)構(gòu)

1.1 CORDIC算法原理

CORDIC算法是由J．Volder于1959年提出的,。該算法適用于解決一些三角學(xué)的問題，如平面坐標的旋轉(zhuǎn)和直角坐標到極坐標的轉(zhuǎn)換等,。C-ORDIC算法的基本思想是通過一系列固定的、與運算基數(shù)有關(guān)的角度的不斷偏擺以逼近所需的旋轉(zhuǎn)角度,。從廣義上講,，CORDIC方法就是一種數(shù)值計算的逼近方法。該算法實現(xiàn)三角函數(shù)的基本原理如圖1所示,。

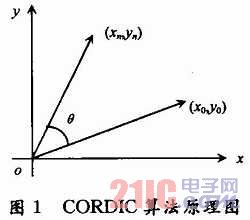
設(shè)初始向量(x0,，y0)逆時針旋轉(zhuǎn)角度θ后得到向量(xn，yn),，如圖1所示,。則：

為了避免復(fù)雜的乘法運算，用一系列微旋轉(zhuǎn)來處理,，第i次旋轉(zhuǎn)可表示為：

式中：θi表示第i次旋轉(zhuǎn)的角度,，并且滿足tanθi=2-i；zi表示第i次旋轉(zhuǎn)后與目標角度的差,；δi表示向量的旋轉(zhuǎn)方向,，由zi的符號位來決定，即δi=sign zi,。為每一級的校正因子,，也就是每一級旋轉(zhuǎn)時向量模長發(fā)生的變化，對于字長一定的運算,，總的校正因子是一個常數(shù),。若總的旋轉(zhuǎn)次數(shù)為n，則總校正因子用k表示為：

由式(7)可知：xn,，yn分別為輸入角θ的余弦和正弦值,，故基于CORDIC算法可產(chǎn)生正弦載波信號，而且由式(5)可以看出所有運算簡化成加減法和移位操作,，因此很容易用硬件實現(xiàn),。

1.2 CORDIC流水線結(jié)構(gòu)

CORDIC算法的實現(xiàn)方式有2種：簡單狀態(tài)機法和高速全流水線處理器法。如果計算時間的要求不嚴格,，可以采用狀態(tài)機結(jié)構(gòu),。這一結(jié)構(gòu)中最復(fù)雜的就是兩個桶狀移位器，而桶狀移位器的面積大約和它所包含的傳輸門的數(shù)目成正比,。盡管可以通過改進CORDIC算法來減小CORDIC處理器的總面積,，但桶狀移位器所占的面積并不能減小,。另外，這種結(jié)構(gòu)由于只在時間上復(fù)用資源,，因此,，數(shù)據(jù)吞吐率不高。

由于CORDIC算法的內(nèi)部數(shù)據(jù)流規(guī)則,，決定了在CORDIC處理器解決方案中非常適合采用流水線型微旋轉(zhuǎn)結(jié)構(gòu),。采用流水線可將一個算術(shù)操作分解成一些小規(guī)模的加減法和移位操作，并在多個比較高速的時鐘內(nèi)完成,。另一方面,，輸出信號的精度只與CORDIC算法的旋轉(zhuǎn)次數(shù)或流水單元數(shù)有關(guān)，即與級數(shù)有關(guān),。如需提高精度,，只需簡單地增加流水單元即可，其擴展性很好,，而且這并不會大量增加FPGA的資源耗費,。CORD-IC流水線結(jié)構(gòu)的每一級迭代旋轉(zhuǎn)的硬件實現(xiàn)基本單元如圖2所示。

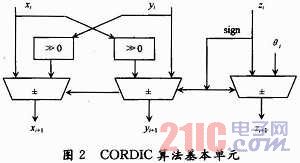
2 基于CORDIC算法正弦載波發(fā)生器的總體結(jié)構(gòu)

正弦載波發(fā)生器系統(tǒng)結(jié)構(gòu)如圖3所示,。

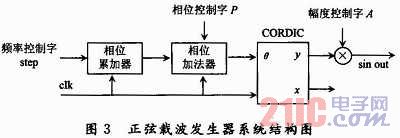
在該系統(tǒng)結(jié)構(gòu)圖中,，CORDIC計算單元是核心。CORDIC計算單元的輸入由相位加法器提供,。相位加法器不間斷地產(chǎn)生角度值,，由CORDIC計算單元計算出相應(yīng)的三角函數(shù)值，即可在其輸出端產(chǎn)生連續(xù)的數(shù)字正弦載波,。

通過頻率控制字,，改變相位累加器的步長，這樣即可改變正弦載波的頻率,。具體的數(shù)學(xué)推導(dǎo)如下：

設(shè)相位累加器的字長為N,，頻率控制字即步長為step，則2N就相當(dāng)于2π rad,，N位中的最低有效位相當(dāng)于2π/2N rad,，即最小的相位增量，step對應(yīng)的相位為step×(2π/2N)rad,，完成一個周期的正弦載波輸出需要2N/step個參考時鐘周期,。所以輸出正弦載波的周期為：

可見改變相位累加器的步長step，可以改變正弦載波的頻率,；改變相位累加器的字長N,，可控制正弦載波的頻率分辨率。在相位累加器后加入相位加法器，通過改變相位控制字P,，可以控制輸出信號的相位,；通過設(shè)置幅度控制字A，可控制最終輸出的正弦載波的幅度大小,。因此,，通過對相位控制字、頻率控制字或幅度控制字進行多路選擇,，可以形成不同進制的調(diào)制方式,。可以看出,，使用該結(jié)構(gòu)可以很容易實現(xiàn)頻率調(diào)制,、相位調(diào)制和幅值調(diào)制。

3 2FSK調(diào)制器的FPGA設(shè)計

圖4為2FSK調(diào)制器頂層工程原理圖,。該原理圖主要由三個模塊組成：2選1數(shù)據(jù)選擇器MUX21、相位累加器adder,、正弦載波生成模塊eor-dic,。其中，clk為系統(tǒng)時鐘信號,，rst為系統(tǒng)清零信號,，step1，step2為2個不同的頻率控制字,，s為系統(tǒng)頻率控制字選通端,。2選1數(shù)據(jù)選擇器的選通端s受基帶信號控制，當(dāng)基帶信號為‘0’時,，選通控制字step1,；當(dāng)基帶信號為‘1’時，選通控制字step2,。通過對step1,，step2的選擇，可以實現(xiàn)頻率的切換,。

在QuartusⅡ環(huán)境中,，三個子模塊均用VHDL語言進行設(shè)計，系統(tǒng)頂層工程采用原理圖進行設(shè)計,，對系統(tǒng)頂層工程進行器件選擇,、引腳鎖定、編譯,、綜合后下載到Cyclone系列EP1C12Q240C8器件中,，通過在頻率控制字的引腳選擇不同參數(shù)即可在FPGA器件中完成2FSK調(diào)制器的設(shè)計。

4 系統(tǒng)硬件實時測試

調(diào)制器的輸出信號為數(shù)字信號,，經(jīng)D/A轉(zhuǎn)換后可以通過示波器進行測試,，也可以直接采用QuartusⅡ軟件中的嵌入式邏輯分析儀Signal-TapⅡ進行測試,。

采用SignalTapⅡ進行芯片測試，用戶無需外接專用儀器,，就可以對FPGA器件內(nèi)部所有信號和節(jié)點進行捕獲分析,，而又不影響原硬件系統(tǒng)的正常工作。經(jīng)測試得到的實時波形如圖5所示,。測試結(jié)果表明,，基于FPGA和CORDIC算法的2FSK調(diào)制器設(shè)計方案是正確可行的，且波形流暢,，在轉(zhuǎn)換處能快速進行切換,。

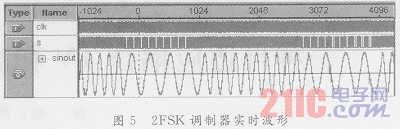
5 結(jié)語

用FPGA和CORDIC算法實現(xiàn)信號調(diào)制，既克服了傳統(tǒng)方法耗費資源,、運行速度低等缺點,，還具有靜態(tài)可重復(fù)編程和動態(tài)在系統(tǒng)重構(gòu)的特性，極大地提高了電子系統(tǒng)設(shè)計的靈活性和通用性,，大大縮短了系統(tǒng)的開發(fā)周期,。

作者：雷能芳 渭南師范學(xué)院   來源：現(xiàn)代電子技術(shù)