0 引言
    PID控制器因算法簡單、魯棒性好,、可靠性高,，一直是工業(yè)生產(chǎn)過程中應用最廣的控制器。然而，實際生產(chǎn)過程往往具有非線性,、時變不確定性,，應用常規(guī)PID控制不能達到理想的控制效果。這時,，往往不得不采用模型預測控制,、自適應控制等先進控制策略來獲得更好的控制性能。但是也存在多種原因阻礙這些先進控制策略在實際中的應用,。其中一個主要的原因就是由于這類先進的控制算法在硬件,、軟件和人員培訓方面缺乏有效的支持，這阻礙了它們在DCS層上的實現(xiàn),。而且在參數(shù)整定方面,，由于這類算法的參數(shù)常缺乏明確的物理意義，對于已熟悉PID參數(shù)整定的操作人員來說,，也是不得不面對的問題,。因此，近年來越來越多的研究人員就上層采用模型預測控制這類先進的控制算法,，而底層保留傳統(tǒng)的PID控制算法,，即所謂的預測PID控制算法，展開了一系列的研究,。如P．Vega等人直接將經(jīng)典PID的參數(shù)引入到性能指標中,，再通過Taylor近似處理得到了次優(yōu)化的控制器參數(shù)。Miller提出了一種隨機預測PID控制算法,，其在數(shù)學上等于穩(wěn)態(tài)加權(quán)廣義預測控制算法,，并先后成功應于化肥廠熱交換器的溫度控制和廢水裝置溶氧濃度的控制。在文獻[5]中,，MASARU KATAYAMA根據(jù)PID與一般GPC控制律之間的對應關(guān)系,，直接計算出PID參數(shù)的值，本文在其基礎(chǔ)上,，采用階梯式策略,，避免了參數(shù)整定過程中復雜的矩陣求逆運算，并給控制輸出引入較強的階梯約束,，改善了控制性能的調(diào)節(jié)靈活性,。另外，文中分析了該方法在整定大延時對象的控制器參數(shù)時所引起的誤差的原因,，并通過引入smith預估器,，有效地改善了這類系統(tǒng)的控制效果。

1 整定算法
1．1 系統(tǒng)描述及PID控制律介紹
    考慮到GPC算法的需要,，本文采用受控自回歸積分滑動平均模型(CARIMA)描述被控對象：
    
    其中,，y(t)和u(t)為系統(tǒng)在t時刻的輸出值和控制量,；ζ(t)為零均值、方差有界的白噪聲,；k為系統(tǒng)的最小時延,；△=1-z-1為差分算子；A(z-1),、B(z-1)分別為后移算子z-1的na和nb階多項式,，且A(z-1)為首一多項式。
    文中控制器采用I-PD型結(jié)構(gòu),，該控制律在改變設(shè)定值時,，控制器輸出不至于有太大的變化，增強了系統(tǒng)的抗擾動能力,，另外可以很方便地得到此I-PD控制律與GPC控制律之間的聯(lián)系,，從而可以依據(jù)GPC思想來進行PID參數(shù)的整定。其具體形式為：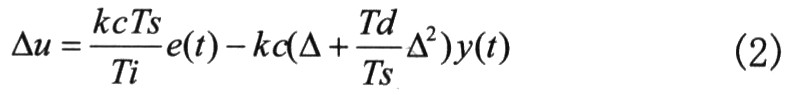
    
    其中,，e(t)=w(t)-y(t)為誤差信號,，w(t)為參考信號，kc,、Ti,、Td分別為比例增益,、積分時問和微分時間,，Ts為采樣時間。對上式進行展開整理可得如下形式：

1．2 SGPC算法
    按照GPC的一般理論,，由模型(1)和Diophantine方程,，得到t時刻對未來t+k+i(i=0，1,，L,，P-1)時刻系統(tǒng)輸出的最優(yōu)預測：

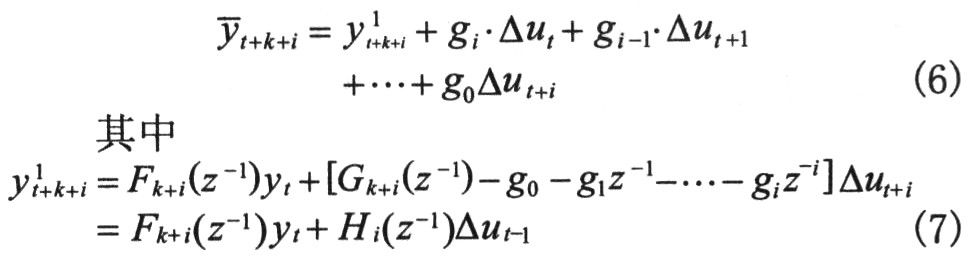
    為最優(yōu)預測中的自由響應部分，F(xiàn)k+i(z-1)和Gk+i(z-1)是由Diophantine方程確定的z-1的多項式,，是對象階躍響應的第l項系數(shù),，可以寫成矩陣形式Y(jié)=Y1+G·△U，則實際的輸出為Y＝Y(jié)＋E,，E為誤差向量,。

    GPC一般性能指標為

   
    其中△U1=(△ut△ut+1…△ut+m-1)，m為控制步長,，λ為控制增量的權(quán)重,。

  由上述各式，根據(jù)傳統(tǒng)的GPC算法,，令J對△U1的偏導數(shù)為0,，可以得到一個控制量序列[6,，9]，為簡化計算,，Diophantine方程一般用遞推算法求解,，但仍然不能避免矩陣求逆，計算量大,，且不能保證矩陣可逆,，計算中還會出現(xiàn)數(shù)值病態(tài)問題，在實際應用中存在著較大的安全隱患,。
    為避免傳統(tǒng)GPC中的矩陣求逆問題,，在算法中引入階梯式策略[6]。令

    由Diophantine方程可知F(1)=Q,，因此式(13)亦可表示為式(5)的形式,，此時

1.3 整定結(jié)果

    由式（4）與式（14）的對應關(guān)系，我們可以比較得到PID控制器各參數(shù)（其中Ts為采樣周期）如下：

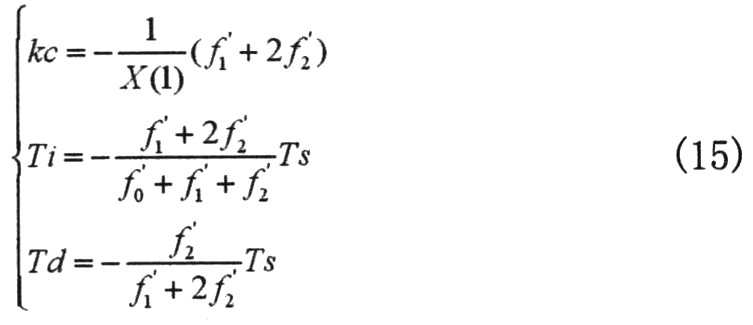
2 整定算法的分析

2.1  參數(shù)調(diào)節(jié)的問題

本文通過引入階梯因子,，避免了參數(shù)整定過程中矩陣求逆,，大大簡化了計算。同時,，在實際系統(tǒng)中,，由于執(zhí)行機構(gòu)性能的限制，若控制量變化頻率高,，不僅執(zhí)行機構(gòu)動作跟不上,，起不到作用，而且會增加執(zhí)行機構(gòu)的磨損,。而階梯式策略假定控制增量服從一個等比序列,，這相當于給控制增量加了一個較強的限制。另外,，由于引進階梯因子后,，加權(quán)因子λ性能的影響減小，而且其對于控制量的抵制作用也變得比較復雜,，因此我們主要可以通過β來調(diào)節(jié)對應PID控制器的魯棒性與快速性,。

2.2 整定誤差的Smith補償

    在前述的算法推導中，可以發(fā)現(xiàn),，為了建立I-PD與SGPC之間的相互聯(lián)系,，對多項式X（z-1）進行了靜態(tài)處理，由式（12）與 式（13）可以看出,，這樣的處理,，相當于認為過去k+nb-1步的輸入變化量都相等，且等于當前時刻的輸入變化量,，即△ut-knb+1=△ut-k-nb+2=…=△ut,，而實際運行中,，在系統(tǒng)動態(tài)響應階段，這種關(guān)系顯然總是不成立的,。這種近似處理,，在系統(tǒng)無延時或小延時，即k取值很小時,，影響可以忽略,，但隨著時延步數(shù)的加大，這種處理對系統(tǒng)魯棒性地影響必將逐漸加劇,，所以需要對具有大延時的系統(tǒng)進行補償,。因此，本文在系統(tǒng)中引入Smith預估器,，以消除系統(tǒng)的時延影響,，改善大延時系統(tǒng)的控制效果。

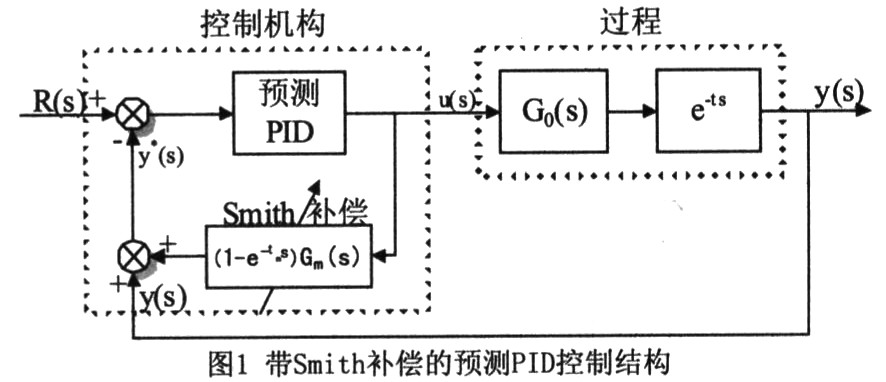
    由于常規(guī)Smith預估器在模型失配時存在低魯棒性問題,，因此在應用中可采用文獻[8]中的自適應方案,，即首先通過單變量尋優(yōu)方法估計實際過程的純滯后，然后再用帶遺忘因子的最小二乘法辨識過程模型的其他參數(shù),，以在線修正模型,。這樣系統(tǒng)的控制結(jié)構(gòu)可以設(shè)計成圖1所示的形式。從圖中可以看出,，若系統(tǒng)無延時,，系統(tǒng)等同于簡單的預測PID控制回路，而當系統(tǒng)有時延時,，延時對系統(tǒng)的影響即可由smith預估器消除,，而預測PID參數(shù)則僅需根據(jù)無時延模型Gm(s)來整定,，這樣就可以避免時延帶來的參數(shù)整定誤差,。

3 仿真及分析
    為仿真需要，考慮以下單變量模型：

   
P=10,，m=5,，λ=1，B與k的值按仿真需要選取,。

    圖2所示為K=7,，β分別取0．75、0．95,、1．05與1．15時,，PID控制系統(tǒng)(無Smith補償)的響應輸出曲線，從圖中可見,，基于SGPC整定的PID控制器的動態(tài)性能可以很容易地通過選擇不同的B值來調(diào)節(jié),，以獲取合適的控制器參數(shù),，隨著B取值的增加，系統(tǒng)的超調(diào)越小,，響應速度則越慢,，充分保持了SGPC控制的這一特點。

  圖3中,，在110s處設(shè)定值發(fā)生幅值為20％,、寬度為10s的脈沖擾動，以及在200s處,，對象模型躍變?yōu)锳1(z-1)=1-0．99z-1+0．25z-2,，以及B1(z-1)=0．57+O．31z-1。從圖中結(jié)果的對比可以看出,，預測PID(β=0．95)比常規(guī)PID(Z-N法整定)控制器具有更好的動態(tài)響應特性,，并且在出現(xiàn)外部擾動以及對象內(nèi)部特性發(fā)生變化時體現(xiàn)出了更強的抗干擾性與魯棒性。

    圖4則是在其他參數(shù)保持不變(β=1．35),，時延步數(shù)分別取值為5,、20、40與110時,，系統(tǒng)(無Smith補償)的響應特性曲線,，可以發(fā)現(xiàn)，隨著時延的增加,，系統(tǒng)的超調(diào)量及響應時間都有所增加,，動態(tài)性能逐漸變差。由前文的分析可知,，系統(tǒng)的動態(tài)響應性能可以通過改變β的大小來調(diào)節(jié),，另外在大時延系統(tǒng)中也可以通過引入Smith預估器來補償時延，這里以k=110為例,，對這兩種方法進行比較,，結(jié)果如圖5所示(800s處模型躍變?yōu)锳1(z-1)，B1(z-1)以及時延k變?yōu)?00),。很顯然,，增加B的值，雖然可以很好地改善系統(tǒng)的超調(diào)量,，但卻無法兼顧系統(tǒng)的響應時間,，這對于那些對系統(tǒng)超調(diào)及響應時間都有要求的對象來說是不可取的，而加入Smith預估補償?shù)姆椒?，則可以消除延時的影響,，使大時延系統(tǒng)的超調(diào)量及響應速度都得到大大改善，并且很好地保持了系統(tǒng)的魯棒性,。

4 結(jié)論
    文中討論了基于SGPC的PID參數(shù)整定問題,。仿真結(jié)果表明,，此方法較常規(guī)PID具有更好的控制性能，而且自適應Smith預估器的引入可以克服大時延系統(tǒng)的整定誤差,，并且充分保持了系統(tǒng)的魯棒性,。本研究為工業(yè)過程控制中的大滯后、時變等復雜系統(tǒng)的控制提供了一種良好的選用方案,。