1 引言
筆者多年研究軟起動器,，發(fā)現(xiàn)軟起動器對電動機的過載保護有些簡單化，雖然說是反時限保護,，但實際是采用定時分段的辦法,，有時誤動作，有時燒電動機,。對于電動機斷續(xù)過載保護時由于電動機早已過熱,，那么它的過載能力已經(jīng)減小，對于冷態(tài)的電動機來說,，它的過載能力要比熱態(tài)的電動機過載能力大的多,。如果要真正反應(yīng)電動機的過載能力又能對電動機起到過載保護就必需通過熱積分，采用熱記憶功能,。這樣才能保正系統(tǒng)的可靠性和保護的靈敏性,。
1.1 兩種典型的數(shù)學模型
軟起動器對電動機具有控制、保護,、監(jiān)測等功能,，對電動機的熱過載保護采用的反時限保護特性有多種數(shù)學模型，其中典型的有兩類：
1.2 脫扣器的控制方式
脫扣器的控制方式可采用：
?。?）查表法
設(shè)定I—t對照表,，根據(jù)當前I控制動作時間t。
但是在實際運行中兩種方法均存在弊端,。如用積分法上述的兩類數(shù)學模型都可能造成在低于動作值時仍能誤動作,；如用查表法在通常電流不斷變化的情況下，很難合理的控制過載脫扣的延時時間,。
為了較好的解決低壓斷路器的智能控制器中長延時脫扣器的延時控制,，本文試圖按熱保護的基本原理進行分析和探討。
2 熱保護的基本要求
根據(jù)熱平衡關(guān)系,，電氣設(shè)備的發(fā)熱應(yīng)等于散熱與蓄熱之和,，即
按電動機起動器和斷路器的要求，k2應(yīng)分別小于1.2和1.3,，為同時滿足這兩種要求,，并留有裕度，可取k2=1.1～1.15。
由式（11）可取
4.3 延時時間的計算
按式（13）計算在不同過載電流下的延時時間,，并考慮電流測量誤差的影響,，計算結(jié)果見表1（計算時取T=642s）。
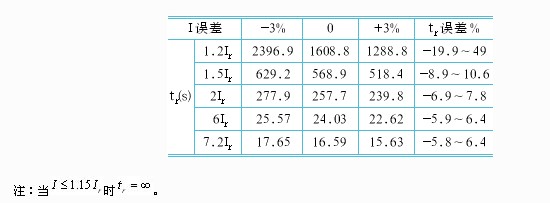
表1 不同過載電流下的延時時間的計算值
5 動作值的測量和計算
為測量智能脫扣器實態(tài)通電時的A值,，可以采用數(shù)值積分的方法等間隔的測量電流和計算A值并與K值比較,。
設(shè)測量間隔為Δt,并且初始溫升為0，由式(6)和(7)
A0=0
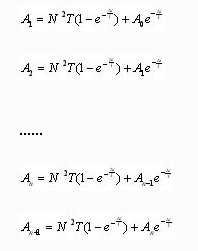
上列各式中N可以為變量,。
逐次計算,，逐次與k比較，直至Ax≥k時控制器動作,。則
在有輔助電源的情況下,，A值逐漸遞減，直至軟起動器重新起動,，A值又開始遞增,；或輔助電源斷開，A值清零,。
為防止過載脫扣后,，軟起動器在短時內(nèi)的再接通并在短時內(nèi)再分斷，可設(shè)置一定的恢復(fù)時間,，以保證在恢復(fù)時間內(nèi),，軟起動器不得起動。
6 測量誤差分析
對式（8）微分：
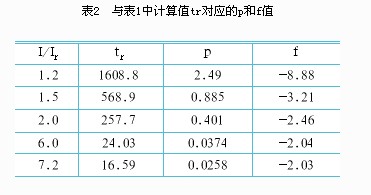
表2的誤差傳遞系數(shù)f的估算值與表1的計算結(jié)果基本相符,。
由表1及表2可以看出在較低過載倍數(shù)下由電流測量誤差所引起的延時時間誤差較大,。
7 保護特性的斜率調(diào)節(jié)
7.1 建立數(shù)學模型
為了滿足不同的配合需要，現(xiàn)在有的制造廠提供了改變長延時保護特性斜率的調(diào)節(jié)功能[2]或參照IEC 60255標準提供了不同數(shù)學模型的保護特性,。為了實現(xiàn)保護特性的斜率調(diào)節(jié),，本文推薦兩種數(shù)學模型并用的方案。
?。?）基本數(shù)學模型
經(jīng)對比分析我們可以以式（7）作為基本保護特性的基本數(shù)學模型,。
（2）用于斜率調(diào)節(jié)的數(shù)學模型
可選用國家標準GB 14598.7（等同IEC 60255-3）推薦的數(shù)學模型用于斜率調(diào)節(jié),。根據(jù)GB 14598.7：
7.2 動作值的測量和控制
將式（17）,、（18）、（19）變換為
A=t(N0.02-1) （20）
A=t(N-1) （21）
A=t(N4-1) （22）
在實際運行中可每經(jīng)過一個等間隔Δt進行一次累加,，逐次計算A值,，逐次與K值比較，直至達到設(shè)定值K值,，求出延時時間tr,。
以式（21）為例,，設(shè)
對應(yīng)式（20）和（22）可以采用同樣方法進行計算和控制。
但是應(yīng)用此方法計算有兩個問題需要解決：
?。?）設(shè)定N的閾值
通常在K的設(shè)定值范圍,，在N=1.05的條件下，計算值tr很可能小于1h,，不能滿足軟起動器要求,。為了防止在1.05Ir及以下的誤脫扣，需設(shè)定閾值,如設(shè)定Nd=1.15,，當N≤Nd時可仍按基本數(shù)學模型控制和計算,。
（2）閾值上下數(shù)學模型的轉(zhuǎn)換
如在N>Nd時,，按式（20)～(22）的數(shù)學模型進行計算和控制。
現(xiàn)舉例說明如下
保護特性取式（21）,，設(shè)定K=13.5
根據(jù)式（12）計算T值,，取k2=1.15
T=13.5/1.152=10.2
在N≤Nd時按前面第4節(jié)所述方法進行計算和控制。
在N>Nd時按式（21）的數(shù)學模型進行計算,，如果在尚未達到動作值時電流又下降使N≤Nd,，并且當前A值為Ay。則此后需按基本數(shù)學模型累加計算A值：
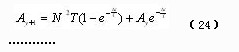
式中初始值A(chǔ)y為原數(shù)學模型下保留的A值,。以下按前面第4節(jié)所述方法進行計算和控制,。
如果此后又回復(fù)N>Nd條件，應(yīng)重新按式（21）的數(shù)學模型計算和控制,。在反復(fù)轉(zhuǎn)換數(shù)學模型時不需改變K值和當前的A值,。
保護特性取式（22），設(shè)定K=1200
根據(jù)式（12）計算T值,，取k2=1.15
T=1200/1.152=907.4
在N≤Nd時按前面第4節(jié)所述方法進行計算和控制,。
在N>Nd時按式（22）的數(shù)學模型進行計算，如果在尚未達到動作值電流又下降至N≤Nd,，并且當前A值為Ay,。則需按式（24）計算A值。
如果此后又回復(fù)N>Nd條件,，應(yīng)重新按式（22）的數(shù)學模型計算和控制,。在反復(fù)轉(zhuǎn)換數(shù)學模型時不需改變K值和當前A值。
7.3 誤差分析
對式(16)微分
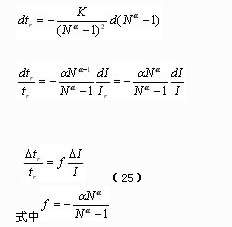
式（19）,、（20）和（21）三種數(shù)學模型時間相對誤差與電流相對誤差之間的傳遞系數(shù)計算值見表3,。
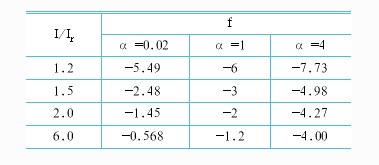
表3 三種數(shù)學模型時間相對誤差與電流相對誤差之間的傳遞系數(shù)計算值
由表3中可見，當α=0.02和α=1時在Nr≥1.5的情況下,，要滿足延時時間的誤差不超過±10%的要求并不困難,；但是在α=4時,，因特性曲線斜率值大，要達到同樣的指標是有一定難度的,，即使電流測量誤差為±2%,，再考慮K的控制誤差和數(shù)值化整等因素，延時時間的誤差也可能大于±10%,。
8 結(jié)束語
本文提出的一套利用數(shù)值積分法解決反時限保護特性的實時測量和控制方法,，既可比較合理、方便的提供多種保護特性,，又可較好的解決負載不斷變化情況下的熱記憶問題,，還有助于提高長延時控制單元的抗干擾能力。
由于在實時控制中,，微處理器在很短時間內(nèi)無法完成一些函數(shù)的復(fù)雜數(shù)學運算,，本文中的一些計算公式和參數(shù)在工程計算中需要進行了變換和處理，在CMC系列軟起動器中得到了應(yīng)用,，通過實際運行達到了理想的效果,。