《電子技術應用》
您所在的位置：首頁 > 通信與網(wǎng)絡 > 設計應用 > 基于對角加載奇異值分解的波束形成算法
基于對角加載奇異值分解的波束形成算法
來源：電子技術應用2012年第7期
曾召華,， 梁文娟
西安科技大學 通信與信息工程學院, 陜西 西安 710054
摘要： 在自適應波束形成算法中,，QR分解具有很好的數(shù)值特征和固有的高度并行性。但當采樣數(shù)較少,，采樣協(xié)方差矩陣估計值的噪聲特征值分散會導致波束形成算法的性能下降問題，QR算法的性能就會下降,。針對此缺陷,，提出了對角加載奇異值（DSVD）分解的算法，該算法先對采樣數(shù)據(jù)所構成的矩陣進行重構,、分解,、再重構、再分解,最后實現(xiàn)對角加載,。通過仿真結果可以看到,DSVD算法不僅避免了對陣列協(xié)方差矩陣的估計和求逆,而且減少了估計運算量和估計誤差,，在復雜度與性能之間進行折衷。
中圖分類號： TN929.5
文獻標識碼： A
文章編號： 0258-7998(2012)07-0107-03
Beamforming algorithm based on diagonal loading singular value decomposition
Zeng Zhaohua, Liang Wenjuan
Department of Communication and Information Engineering, Xi′an University of Science and Technology, Xi′an 710054, China
Abstract： In the adaptive beamforming algorithm，QR decomposition algorithm has better numerical characteristics and inherently high degree of parallelism,。But when the smaller sample number, the noise eigenvalue dispersion of the sample covariance matrix leads to the degradation of the beamforming algorithm performance,，and QR algorithm performance will be decreased. According to this shortcoming, the diagonal loading singular value decomposition algorithm(DSVD) which is proposed in this paper, In this algorithm, the matrix which is composed of sampled data is firstly reconstruction, decomposition, then reconstruction, and then decomposition，and finally do the diagonal loading. DSVD algorithm avoid the estimation and inversion of the array covariance matrix, reducing the estimated computation and estimation error and improving numerical stability, can be obtained tradeoff between complexity and performance.
Key words : beamforming,； QR decomposition algorithm,； diagnoal loading； DSVD

    隨著移動通信的發(fā)展,，TD-SCDMA智能天線中,，下行采用波束形成技術，提高下行信干比,，增強覆蓋,。在3GPP LTE 協(xié)議TS 36.213 Release 8中定義了7種下行發(fā)射模式，其中模式7為單天線端口（端口5）即為通常所述的波束賦形模式[1],，主要用途是提高SINR,、增加小區(qū)的覆蓋范圍。LTE標準支持波束形成技術,，該技術是針對基站使用小間距的天線陣列,，為用戶形成特定指向的波束。

    采樣矩陣求逆（SMI）算法是自適應波束形成中常用的方法,，它收斂快,，干擾抑制效果好。在數(shù)值分析中,，SMI算法要估計接收信號的自相關矩陣,，自相關矩陣的特征值的分散度(條件數(shù)) 要大于數(shù)據(jù)矩陣本身，條件數(shù)越大,，數(shù)值魯棒性越差,，顯然任何一種不求自相關矩陣而直接對數(shù)據(jù)矩陣計算的算法都會得到較SMI好的數(shù)值特性[2]。QR分解,，它通過對輸入數(shù)據(jù)矩陣做QR分解完成協(xié)方差矩陣的估計,，進而求得權向量，具有更好的數(shù)值特性和固有的高度并行性[3],，因此在實際的各種系統(tǒng)中得到了廣泛的應用,。但當采樣數(shù)較少，采樣協(xié)方差矩陣估計值的噪聲特征值分散會導致波束形成算法的性能下降問題,。
    針對此缺陷,，本文提出了對角加載奇異值（DSVD）分解的算法，該算法首先對采樣數(shù)據(jù)矩陣進行奇異值（SVD）分解,，再利用對角加載技術能減弱小特征值對應的噪聲波束的影響這一優(yōu)勢,，實現(xiàn)對角加載,，DSVD算法不僅提高了算法的性能而且降低了復雜度。


3 仿真結果
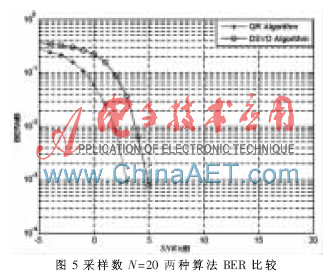
    仿真條件：假設信號的波達方向為0°,，干擾源的波達方向分別為50°（干擾噪聲比為30 dB）SNR=20 dB,。圖1為采樣數(shù)N=300 QR分解算法和DSVD分解算法的陣列方向圖；圖2為采樣數(shù)N=30 QR分解算法和DSVD分解算法的陣列方向圖,；圖3為QR分解算法和DSVD分解算法的陣列輸出SINR隨采樣數(shù)的變化曲線,；圖4為采樣數(shù)N=20 的QR分解算法、DSVD算法的陣列輸出信干噪比SINR隨信噪比SNR的變化曲線,；圖5為采樣數(shù)N=20 的QR分解算法與DSVD算法的BER比較圖,。

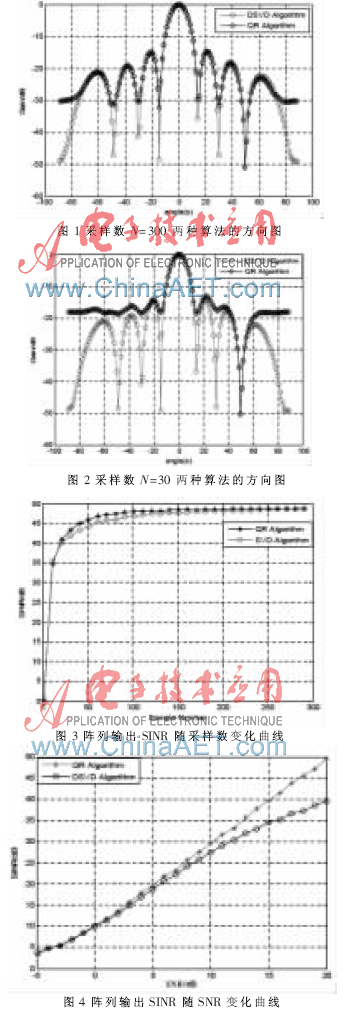
    從圖1可以看出，在采樣數(shù)較大的情況下,，兩種算法的方向圖都在期望信號處形成了很高的增益,，達到了提取期望信號的目的，在干擾方向50°上都形成了零陷,，抑制了干擾,，兩種算法形成的零陷一樣深。從圖2可以看出,，在采樣數(shù)較少的情況下,，QR分解算法的旁瓣較高，其性能很不理想,，但DSVD算法的旁瓣都較低,，對旁瓣性能的改善非常明顯。從圖3可以看出,，文中的QR分解算法和DSVD分解算法都有很高的輸出SINR,，而且這兩種算法的輸出SINR接近，對角加載的算法在采樣數(shù)較少的情況下的就有很好的性能,，且其性能優(yōu)于沒有進行對角加載的算法的性能,。從圖4也可以看出，對角加載SVD算法的輸出SINR高于QR算法的SINR,。再結合圖5,，可以得出DSVD算法的性能優(yōu)于QR算法的性能，可以提高波束形成算法的性能,。

    在自適應波束形成算法中,，QR算法優(yōu)于SMI算法，提高了數(shù)據(jù)魯棒性,。DSVD分解算法和QR分解算法都有很好的性能，能實現(xiàn)正確的波束形成,，提高系統(tǒng)增益,。仿真結果證明了在采樣數(shù)較少的情況下，通過DSVD算法，降低了小特征值及其特征向量的擾動,，使DSVD分解算法的性能優(yōu)于QR分解算法的性能,。
參考文獻
[1] 曾召華.LTE基本原理與關鍵技術[M].西安: 西安電子科技大學出版社, 2010.
[2] 張引，黃建國.基于特征結構的可變對角加載波束形成算法[J].電聲技術,2008,32(11):61-64.
[3] 倪淑燕,，程乃平,，倪正中.固定樣值數(shù)目的QR分解遞推算法[J]. 通信學報，2010,31（8A）：195-200.
[4] Yuen Chau, Sun Sumei, Zhang Jiankang.Comparative study  of  QRS in closed-loop beamforming systems[J]. in Proceedings of the IEEE Military Communications Conference, Orlando, FL, Oct. 2007.
[5] CARLSON B D. Covariance matrix estimation errors and diagonal loading in adaptive arrays[J]. IEEE Trans, Aerospace and Electronic Systems, 1988, 24(4)：397-401.

此內容為AET網(wǎng)站原創(chuàng),，未經授權禁止轉載,。