文獻標識碼： A
文章編號： 0258-7998(2012)10-0009-03
在對數(shù)字圖像進行多分辨率觀察和處理時,，離散小波變換（DWT）是首選的數(shù)學工具,。小波提升算法[1]作為小波變換的快速實現(xiàn)方法，使濾波過程被分解為幾個提升步驟,，運算量大為減少,，便于實現(xiàn)即位計算，同時節(jié)省了存儲空間,，非常適合進行硬件實現(xiàn),。
目前普遍應用的實現(xiàn)二維提升小波變換的硬件架構包括基于幀的硬件架構和基于行的硬件架構[2]。隨著大量相關研究工作[3-5]的不斷進行,，新的VLSI架構不斷產(chǎn)生,，電路整體性能逐漸提高，但在降低電路控制復雜度和對存儲空間的耗費的兼顧上仍存在不足,。本文提出一種直接二維提升小波變換VLSI架構,，可有效降低控制電路的復雜度，明顯地節(jié)省片上存儲空間,，使得設計的電路具有較好的綜合性能,。
1 小波提升算法
1.1 提升小波變換
通過提升框架實現(xiàn)小波變換分為三個步驟：分裂、預測和更新[3],。離散情況下,，給定輸入的離散信號數(shù)據(jù)集pk(pk代表序列p中的第k個數(shù))，并將其分為奇數(shù)集合和偶數(shù)集合,，經(jīng)過完整提升步驟后,，分解成數(shù)據(jù)集sk和dk。其中sk表示尺度系數(shù),，dk表示小波系數(shù),。以Le Gall 5/3小波為例，1-D整數(shù)小波變換分解步驟如圖1所示,。
完成二維變換過程如下：圖像在經(jīng)過一次行變換后
同理,，為獲得先高通后低通濾波結果HL,、先低通后高通濾波結果LH及兩次高通濾波結果HH數(shù)據(jù)，可將式(1)和式(3)通過同樣的方式應用于二維變換,。以行列式方式表達,，如圖3(b)、(c),、(d)所示,。
2 架構設計
2.1 整體架構
對于2-D DWT，本文以圖3推導出的公式為基礎,，設計直接進行二維變換的提升小波變換實現(xiàn)方式,。系統(tǒng)結構框圖如圖4所示。圖像數(shù)據(jù)從外部存儲器中讀出,，經(jīng)地址拓展單元進行邊界延拓后,，寫入緩沖單元；之后將數(shù)據(jù)送入二維DWT處理模塊,，產(chǎn)生4個子帶數(shù)據(jù)，進行降2采樣后,，結果數(shù)據(jù)送至VGA顯示器進行顯示輸出,。系統(tǒng)控制模塊產(chǎn)生各種控制信號約束系統(tǒng)各部分在特定的時序下工作。
2.2 內(nèi)部結構
在進行數(shù)字圖像的二維小波分解過程中,，二維變換處理器是核心,，它將影響整個系統(tǒng)的時序設計和綜合性能。
通過圖3中給出的參數(shù)行列式可以得出結論,，二維變換過程實際上是一個5×5的采樣窗口中數(shù)據(jù)的加權求和,，其包含的運算主要為乘法運算和加法運算。
根據(jù)圖3中行列式參數(shù)二維變換設計處理器具體結構,，如圖5所示,。
該結構包含15個加法器、18個移位器和34個延遲單元(D),，不再需要額外的乘法器,。可以估計,，該一維5/3小波變換架構在FPGA中的實現(xiàn)需要占用邏輯單元數(shù)量約為40A(A為原始數(shù)據(jù)位寬),。完成一幅大小為N×N的圖像的L級分解所需時鐘周期數(shù)為：
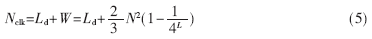
其中，W為除去延時,，處理器進行實際運算產(chǎn)生有效數(shù)據(jù)所需時鐘周期個數(shù),；Ld為行變換和列變換之間的延遲。Ld=0,，即在此過程中行列變換同時完成,，不會產(chǎn)生中間數(shù)據(jù),，節(jié)省了大量片上存儲空間，消除了行列變換的延時,。另外,，外部存儲器讀取次數(shù)有所增加，但處理器工作時間明顯縮短,，大大降低了系統(tǒng)總功耗,。
3 實驗結果和分析
為對本設計中的二維小波變換架構進行功能驗證并直觀地觀察進行小波分解后的圖像效果，通過ModelSim軟件對處理器模塊進行了仿真,，如圖6所示,。
表1分別就所需的硬件復雜度、存儲空間占用量,、延遲時間以及控制電路的復雜度等方面的性能給出本文設計架構與現(xiàn)存其他二維DWT架構的對比情況,。
本文以Le Gall 5/3小波為例，提出了一種直接二維提升小波變換VLSI架構,。作為基于行的變換架構的一種改進,，該架構具有結構簡單、節(jié)省片上存儲空間,、靈活性高等優(yōu)點,，為硬件電路實現(xiàn)二維提升小波變換提出了新的思路。純計算邏輯下,，其處理速度可達到157.78 MHz,。
為對文中提出的架構進行功能驗證，采用Cyclone II系列 FPGA-EP2C35F672C6搭建其硬件電路,。通過實驗證實能較好地完成預定的設計功能,。
參考文獻
[1] SWELDENS W.The lifting scheme：a custom-design construction of biothogonal wavelets[J].Data Compression Conference，1996,，3(2)：186-200.
[2] CHRYSAFIS C,，ORTEGA A.Line based，reduced memory,，wavelet image comperssion[C]．IEEE Trans． on Image Processing,，Washington，DC,，USA,，1998：398-407.
[3] ANDRA K，CHAKRABARTI C,，ACHARYA T.A VLSI architecture for lifting-based forward and inverse wavelet transform[J].IEEE Trans. Signal Process.,，2002，50(4)：966-977.
[4] LIAO H,，MANDAL M K,，COCKBURN B F.Efficient architectures for 1-D and 2-D lifting-based wavelet transforms [J].IEEE Trans. Signal Process.,，2004，52(5)：1315-1326.
[5] BARUA S,，CARLETTA J E,，KOTTERI K A.An efficient architecture for lifting-based two-dimensional discrete wavelet transform，Integr[J].VLSI J.,，2005,，38(3)：341-352.
[6] MAAMOUN M，BRADAI R,，MERAGHNI A,，et al.Low cost VLSI discrete wavelet transform and FIR filters architectures for very high-speed signal and image processing[C].IEEE 9th International Conference on Cybernetic Intelligent Systems，2010：1-6.